复合网络攻击下离散时间多智能体系统的云端预测控制

贾新春,张媛,池小波,阮艺琳

(1.山西大学 自动化与软件学院,山西 太原 030013;2.山西大学 数学科学学院,山西 太原 030006)

0 引言

一致性问题是多智能体系统(MASs)协调控制的关键问题之一,其目的是通过与邻居节点交换信息使得所有智能体达到一个期望的状态。MASs是由空间分布的多个智能体构成。由于具有更好的鲁棒性、灵活性和经济性等特点,MASs被广泛应用于很多领域,如车辆系统[1]、无人机编队控制[2]和智能电网[3]等。

考虑到多智能体系统之间是通过网络来进行信息交互,因此,一些关键问题是不容忽视的,例如网络诱导时延、丢包、量化和安全等，这些因素会使得系统性能下降甚至导致系统不稳定[4]。近年来,相关领域的研究者已经提出了一些动态补偿方法来消除网络诱导时延和数据包丢失等的影响[5-7]。文[5]研究了带有通信时延的网络化离散时间多智能体系统(DMASs)的分布式自适应事件触发预测控制问题。考虑到研究对象为同构MASs,故在文[5]中智能体i可以通过自身的系统矩阵和控制命令对其状态进行预测,且基于接收到的邻居信息来预测邻居智能体的状态。文[6]针对固定网络诱导时延情形,提出了DoS攻击下带有量化信号的网络化多智能体系统的云端预测控制，但并未考虑观测器和控制器所用的控制输入不一致问题。文[7]利用一个比例积分预测控制策略来研究网络化MASs控制问题,其中假设双边网络诱导时延的上界为两侧时延上界之和。基于以上研究和分析,如何提出一种有效的基于预测控制策略的MASs一致性控制方法仍是一个有待解决的问题。

近些年来,由于信息处理和动态过程的紧密耦合,使得MASs在信息的传输过程中特别容易受到网络攻击的影响,进而造成对系统的重大破坏,甚至不稳定。因此,许多学者对安全问题进行了研究[8-11]。文[8]研究了改变网络拓的网络攻击下非线性MASs的分布式事件触发一致性。文[9]针对无领导者和领导者-跟随者一致性问题,给出了对DoS攻击的频率和持续时间的明确分析并提出了弹性协作事件触发控制方案。文[10]研究了一类具有网络攻击和有损传感器的离散时间MASs基于观测器的事件触发一致控制问题,其中考虑的典型网络攻击为欺骗攻击。文[11]针对重放攻击下的一类信息物理系统(CPS)研究了安全分布式卡尔曼融合估计问题。但是在实际的网络系统中,攻击的类型不完全是简单的典型网络攻击,一般来说,恶意的网络攻击往往是更为复杂的、且由多个典型网络攻击在时间或空间上融合形成的。因此,在复合网络攻击下研究MASs的安全控制问题具有很重要的理论价值。

考虑到时变网络诱导时延和复合网络攻击共存的情形下,本文提出了一种新的云端预测控制策略,以保证在复合网络攻击和多率采样机制下MASs的一致性。该策略可以通过使用最新接收的采样数据来补偿网络引起的不确定性的影响并提高控制性能。本文的主要贡献概括如下:

i)通过引入云端模拟攻击机制来补偿观测器和控制器所用的控制输入不一致情形,设计了一种新颖的云端预测控制策略,以补偿网络引起的时延和复合网络攻击。该控制器可以使用最新接收的采样数据来使得所考虑的多智能体预测控制系统实现更好的控制性能。在预测控制中考虑了云控制框架,能大幅度降低计算量,节省网络资源。

ii)相比于现存文献中仅考虑单个典型的网络攻击情形,本文提出一种较符合实际情形的复合型网络攻击模型。

iii)在本文所设计的云端预测控制机制下,MASs的一个稳定性判据被提出来确保智能体达到均方一致性。

1 系统建模与问题描述

本文考虑一个由N个智能体组成的DMASs,其中第i个智能体的动力学方程可描述为：

(1)

yi(t)=Cxi(t),

(2)

αi(t)[Hui(t)+ui(t-θi(t))],

(3)

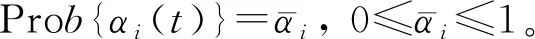
为了便于系统分析,本文给出如下的假设:

假设1传感器组是以一个常数为采样周期按照时间驱动的,控制器和估计器是事件驱动的。智能体所使用的传感器是不相同的,且满足传感器S1的采样周期为T1=r1T0,传感器S2的采样周期为T2=r2T0,以此类推。传感器SN的采样周期为TN=rNT0,其中T0是一个给定的正常数,ri是正整数。

假设2矩阵对(A,B)可镇定,且矩阵对(A,C)可观测。

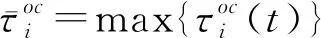
图1 多智能体系统框架Fig.1 The framework of multi-agent system

本文的设计目标是针对DMASs在多率采样机制和时变时延下设计一个分布式预测控制律ui(t)使得如下的一致性被实现:

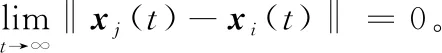
(4)

1.1 观测器设计

本文采用N组采样周期分别为T1、T2和TN的传感器来对每一个智能体的输出进行采样。以智能体i为例, 对应的传感器为Si, 输出信号表示为yi(riT0k),k=0,1,2,…。从假设可以知道, 尽管系统的状态不可测, 但是智能体是可观测的。所以每一个智能体仅使用自己的输出信息对自己的状态进行估计, 计算如下：

(5)

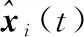
(6)

ei(t+1)=Aei(t)-LCei(t-di(t))。

(7)

1.2 一个改进的云端预测控制器设计

(8)

(9)

其中

…

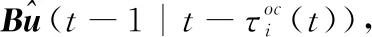
(10)

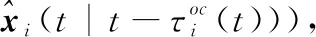
(11)

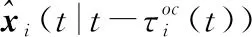
(12)

在第一步中,智能体端需要向预测控制云端发送ACK命令来告知智能体已收到新的数据。第二步:是对前向通道中的时延进行预测补偿,由于前向通道中有网络攻击的影响,在预测控制云端加入了一个模拟网络攻击的装置。在这个装置下前项通道中的预测可以表述为

…

(13)

(14)

(15)

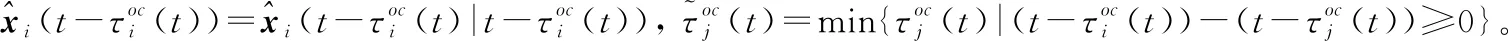
(16)

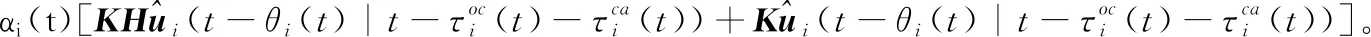
(17)

1.3 闭环系统的构造

对于单个的智能体系统来说,它的闭环系统模型为

(18)

x(t+1)=(IN⊗A+((IN-Λ(t))⊗In)(W⊗BK)x(t)-((IN-Λ(t))⊗In)W⊗BK)e(t)+

[(Λ(t)⊗In)(W⊗BHK)+(Λ(t)⊗In)(W⊗BK)]x(t-θ(t))-

[(Λ(t)⊗In)(W⊗BHK)+(Λ(t)⊗In)(W⊗BK)]e(t-θ(t))，

(19)

其中,

记一个均方状态

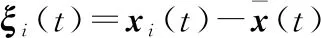
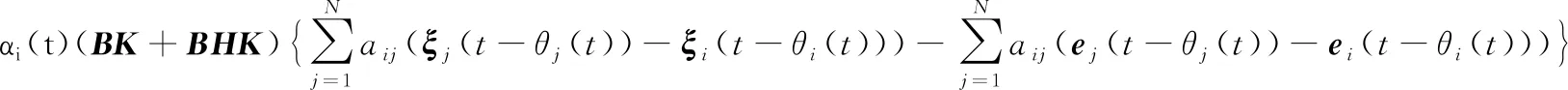
(20)

则整个系统的闭环可以建模为

ξ(t+1)=(IN⊗A-((IN-Λ(t))⊗In)(W⊗BK))ξ(t)-((IN-Λ(t))⊗In)W⊗BKe(t)+

(Λ(t)⊗In)(W⊗(BK+BHK)){ξ(t-θ(t))-e(t-θ(t))}

(21)

增广z(t+1)=[ξT(t+1)eT(t+1)], 则有

z(t+1)=Π1z(t)+Π2z(t-θ(t))+Π3z(t-d(t))

(22)

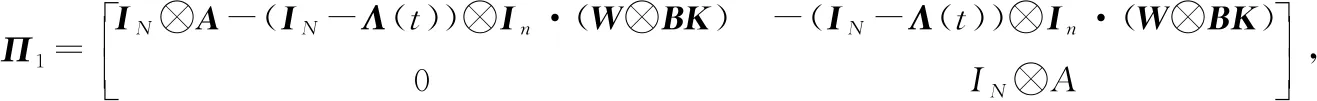
2 主要结论

通过李亚普诺夫函数和LMI方法本节首先给出系统一致性的判据然后给出预测控制器的设计方法。首先取候选Lyapunov函数为

V(z(t))=V1(z(t))+V2(z(t))+V3(z(t))，

(23)

其中,

P1,Q1,Q2是正定Lyapunov矩阵, 在本文中可以设为如下形式P1=diag{P11,P11},Q1=diag{Q11,Q11},Q2=diag{Q22,Q22}。

2.1 稳定性分析

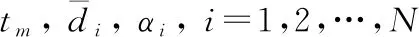
(24)

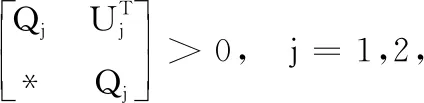
(25)

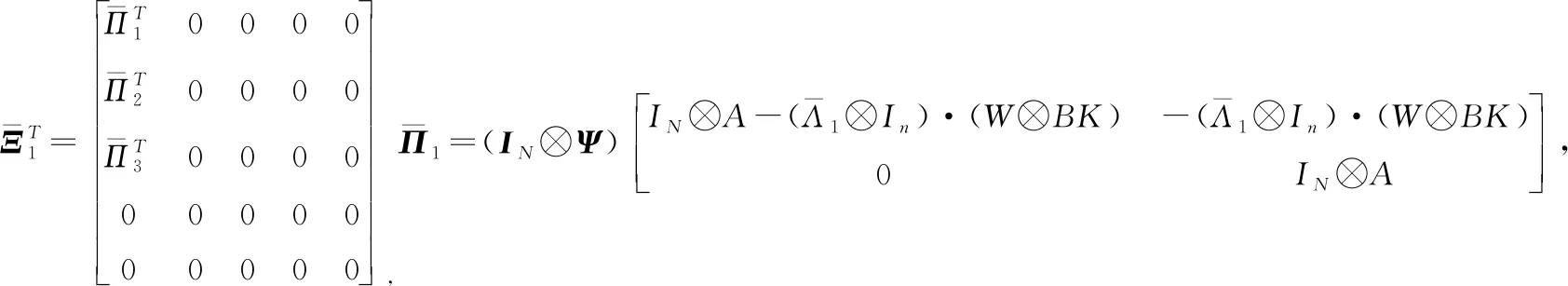
证明对上述(23)所设计的Lyapunov候选函数关于时间求导可得

ΔV1(z(t))=zT(t+1)(IN⊗P1)z(t+1)-zT(t)(IN⊗P1)z(t)，

(26)

ΔV2(z(t))=zT(t)(IN⊗Q1)z(t)-zT(t-tm)(IN⊗Q1)z(t-tm)+

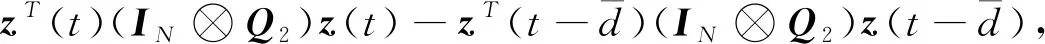
(27)

zT(t)(IN⊗Q1)z(t+1)+zT(t)(IN⊗Q1)z(t))-

zT(t+1)(IN⊗Q2)z(t)-zT(t)(IN⊗Q2)z(t+1)+zT(t)(IN⊗Q2)z(t))-

(28)

通过Jesen不等式可将上式整理为

2.2 控制器设计

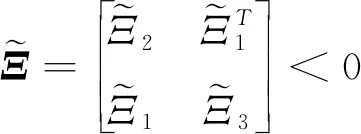
(29)

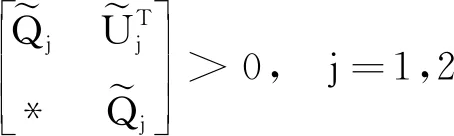
(30)

其中,

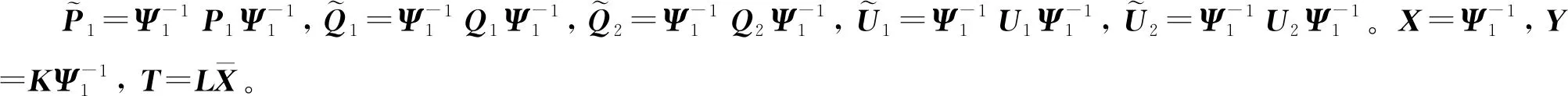
3 仿真实例

考虑如下的离散时间网络化控制系统:

信拓扑所对应的邻接矩阵

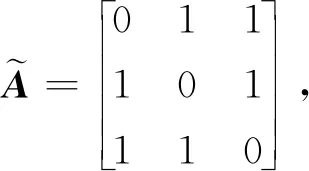
度矩阵

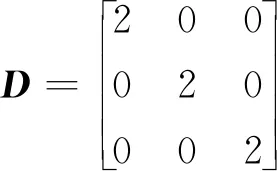
通信拓扑下系统的Laplace矩阵为

多智能体系统的初始条件为

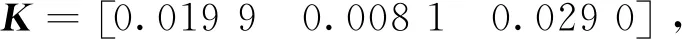
观测器增益矩阵

进而可得在本文的闭环系统状态的轨迹图(图2), 以及状态误差图(图3)。其中,emij(t)表示的是第i个智能体的第j个状态与状态平均值的误差。由图2可知所有智能体的第j个分量均达到了当前时刻它们的状态的平均值(j=1,2,3)。由图3可得所有智能体的第j个分量与状态平均值的误差均趋于零。通过图2和图3中的结果分析可知,基于云端预测控制器(8)-(11)的多智能体系统(1)达到了一致性, 证明了本文所提设计方法的有效性。

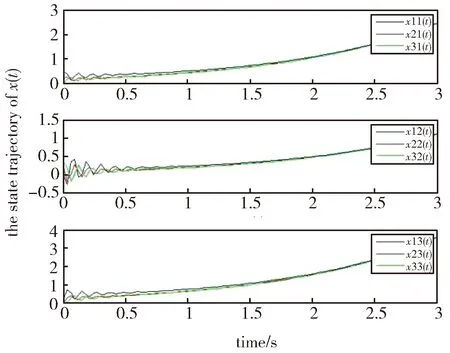
图2 状态轨迹图Fig.2 State locus diagram

图3 状态误差图Fig.3 State error diagram

4 结论

本文研究了非理想网络环境和复合网络攻击下DMASs的均方一致性的云端预测控制。与传统的控制协议不同, 本文所设计云端预测控制协议不但可以对网络诱导时延主动补偿, 而且可以节约网络资源和减少计算量。给出了闭环系统均方一致性的的充分条件，并通过一个数值例子说明了本文研究的方法对保证系统性能是有效的。针对异构多智能体系统在非理想网络环境和多率采样机制下DMASs的一致性问题是我们未来的研究方向。