基于改进DEMATEL的区间对偶犹豫模糊多属性决策方法
2020-09-14杨志辉
杨 悦, 杨志辉, 宋 洋
(东华理工大学 理学院,江西 南昌 330013)
为描述客观世界中亦此亦彼的不确定性现象,美国控制论专家Zadeh(1965)提出了模糊集理论,用隶属度将元素与现象集合建立对应关系。Atanassov(1986)引入非隶属度的概念,将模糊集拓展为直觉模糊集,以反映评价者多维度的偏好信息。Torra(2010)将决策信息与模糊理论相结合,提出了由多个隶属度构成的犹豫模糊集。为兼顾多维偏好,对偶犹豫模糊理论得到了研究人员的广泛关注(Zhu et al.,2012;Wang et al.,2013)。依据决策对象的自有特性以及评价者本身的犹豫属性,区间数代表隶属度与非隶属度的区间值对偶犹豫模糊集被广泛地应用于模糊多属性决策问题(Farhadinia,2014)。Xiao等(2018)研究了区间对偶犹豫模糊不平衡语言集的多属性群决策方法及其应用。杨宗华等(2017)给出了基于IVDHFS不确定语言变量的多属性决策方法。
DEMATEL分析法,又称为“决策试行与评估实验法”,是一种用于解决复杂系统工程问题的整套方法论(Seyed-Hosseini et al., 2006)。因其良好适用性,已有学者就DEMATEL在不同场景下的应用进行了研究。谢晖等(2014)将DEMATEL分析法应用到基于直觉模糊偏好的群组决策;Asan等(2018)给出了基于区间犹豫模糊集的DEMATEL分析方法;杨威等(2018)提出了基于DEMATEL和TOPSIS法的多值中智模糊多属性决策方法;同时,为评价方案间的优劣程度,以TOPSIS为代表的逼近理想解的排序方法,近年被广泛应用到多种模糊决策及对策问题的研究当中(Hajek et al.,2019;Zhang et al.,2019;Wu et al., 2019),为解决具有异质评价信息的管理问题,提供了行之有效的方法。
利用DEMATEL工具加以分析,并对其相应算法做出改进。通过赋予各属性间直接影响程度以强弱指标,定义影响度与被影响度等分析参量,获得了属性集的权重向量。同时,定义了一种广义区间对偶犹豫模糊集的距离,利用加权平均(WA)算子将权重向量与决策矩阵集结,提出了基于DEMATEL的区间对偶犹豫模糊多属性决策方法。最后通过具体实例,验证了该方法的有效性。
1 区间对偶犹豫模糊集及其相关定义
定义1 定义论域X上的区间对偶犹豫模糊集D为(Farhadinia, 2014):
D={〈 (1) 定义2 设D= 定义3 设D〈f,h〉为X上的区间对偶犹豫模糊集,定义得分函数S(D)、精确函数T(D)分别为: (2) (3) 式中,α=1,2,…,m,β=1,2,…,n。l(f)、l(h)分别表示f(x)、h(x)中元素的个数。 对任意两个区间对偶犹豫模糊集D1、D2:若S(D1)>S(D2),则D1>D2。若S(D1)=S(D2),则有:若T(D1)>T(D2),则D1>D2;若T(D1)=T(D2),则D1=D2。 定义4 设D1=〈f1,h1〉,D2=〈f2,h2〉为X上两个区间对偶犹豫模糊集,k为正整数,定义D1与D2的广义相似性s(D1,D2)、距离d(D1,D2)分别为: s(D1,D2)=1-d(D1-D2) (4) d(D1,D2)= (5) 为消除属性间优先级别对多属性决策的影响,将DEMATEL分析法应用到IVDHFS,将属性权重与对应评价值集结以规范决策信息,通过对属性间影响程度加以刻画,引入决策偏好系数,从而导出属性权重的模糊向量,最后配合决策矩阵对方案集进行排序,获得决策方案。 考虑一多属性决策问题,设方案集A=(A1,A2,…,Am),属性集C=(C1,C2,…,Cn)。规定属性Ci(1≤i≤n)对其本身的直接影响程度为0。依据DEMATEL算法中的具体要求,给出如下定义。 定义5 综合得分矩阵T=[tij]n×n各行元素之和为影响度参量,各列元素之和为被影响度参量,即, (6) 式中,ki表示属性Ci对其他属性施加的综合影响值,gi表示属性Ci受到其他属性施加的综合影响值。 定义6ki与gi之和为中心度参量,ki与gi之差为原因度参量,即 mi=ki+gi,ri=ki-gi(i,j=1,2,…,n) (7) 权重决策系数: Ei=ami+bri 式中,a、b为偏好系数(a+b=1且a,b≥0),mi表示属性Ci在属性集中活跃程度,ri表示属性Ci对属性集的净值影响力。针对不同的决策场景,决策人员对属性活跃度及其净值影响力的重视程度存在偏好,因此,可选取不同的a、b值以保证属性权重的准确性。 Step 1 决策人员给出各属性间直接影响矩阵X=[xij]n×n。其中,xij=〈fij(x),hij(x)〉。fij、hij分别表示属性Ci对Cj具有高影响力的隶属度与非隶属度的评价值集合。 (8) Step 3 将规范得分矩阵转化为综合得分矩阵: (9) 式中,I为单位矩阵,(I-S′)-1为矩阵(I-S′)的逆矩阵,tij代表属性Ci对因素Cj的综合影响度得分。 Step 4 分别计算每个属性对应的影响度ki、被影响度gi、中心度mi、原因度ri,建立参量评价列表。 Step 5 计算每个属性Ci的权重wi,构建权重向量W。a,b为决策偏好系数,a+b=1且a,b≥0。 (10) Step 6 决策者给出方案Ai相对属性Cj的区间对偶犹豫模糊评价值rij。fij、hij表示rij中隶属度、非隶属度集合,根据属性类型(效益型U、成本型V),将评价值规范化处理,得决策矩阵R=[rij]m×n: (11) Step 7 引入WA算子,将权重向量W与决策矩阵R集结,得综合决策矩阵R′=R·W=wj·rij。 Step 8 构建区间对偶犹豫模糊矩阵R′的正、负理想解矩阵: (12) (13) (14) 某企业为了扩大生产规模,需筹建一个新的流水车间,现从备选位置中挑选出4个厂区选址。管理层聘请来自不同行业的相关专家组成决策团队,依据区间对偶犹豫模糊集的决策要求,对4个位置分别以地理因素A1、环境因素A2、市场因素A3、政策因素A4等标准加以评价。给出两两属性之间的直接影响矩阵为: 计算并规范得分函数矩阵,利用式(9)将其转化为综合决策矩阵,参评属性值如表1所示。 表1 参评属性值 依据决策场景,这里取a=0.6,b=0.4。得权重向量W=(0.44,0.13,0.24,0.19)T。决策团队给出方案相对属性的IVDHFS评价值rij,规范评价值得决策矩阵R如下: 将W与决策矩阵R集结,得综合决策矩阵R′。利用式(2),(12),(13)计算得R′的正、负理想解矩阵: 计算各方案相对贴进度:ε1=0.047,ε2=0.519,ε3=0.465,ε4=0.382。按照从大到小的顺序加以排列:ε2>ε3>ε4>ε1,得最优方案为方案A2。 本次研究对DEMATEL分析法的改进之处主要分为两部分:①分析要素间影响关系时,将中心度与原因度统一考察,通过引入偏好系数,使其能够适应更加复杂的决策场景;②为避免原因度参量出现负值时导致权重计算出现偏差,可将指数函数引入权重计算模型,重新定义了要素重要度的计算方法。 现参考杨威等(2018)提出的要素权重确定方法,对上述案例加以分析。设决策者给出相同的直接影响矩阵X、方案评价矩阵R,基于上述信息,计算案例中各要素的权重。 (15) 将表1中各参评属性值代入式(15),计算得属性集的权重向量W=(0.25,0.21,0.30,0.24)T,将W与决策矩阵R集结,计算得综合决策矩阵R′的正、负理想解矩阵: 根据定义4计算各方案综合评价值到正、负理想解的距离: 计算各方案相对贴进度:ε1=0.222,ε2=0.539,ε3=0.573,ε4=0.381。按照从大到小的顺序排列:ε3>ε2>ε4>ε1,得最优方案为方案A3。 由上述结果分析,两种权重确定方法得到的评价结果基本一致,说明提出的方法具有一定的稳定性与可行性。两种评价结果的差异性体现在方案A2、A3的排列次序上。其原因归结如下: 笔者提出的方法,能够刻画原因度出现负值时,对元素重要度造成的减弱效果,这更加贴近实际问题中的决策原则。而杨威等(2018)提出的方法,是基于中心度与原因度具备同等决策地位的前提下的。因此,该方法无法对原因度的性质加以区分,例如,当k1=4.13,g1=2.23,k2=2.23,g1=4.13时,利用式(15)计算属性权重得w1=w2,该结果显然缺乏一定合理性。同时,本次研究引入的偏好系数,能有效照顾不同的决策偏好,适应更具一般性的决策问题,决策方法更加科学。 本次研究提出了一种基于DEMATEL的区间对偶犹豫模糊多属性决策方法。该方法综合了DEMATEL分析工具与传统距离测度的分析优势,通过对属性进行多参量刻画,引入决策偏好系数,提出了新的权重确定方法。同时,定义了一种IVDHFS广义距离测度,应用加权平均(WA)算子将初始决策矩阵转化为综合决策矩阵,计算得各方案相对贴近度,完成最终的方案排序。新的方法在保证数据完整性的同时,可有效减少计算流程,尤其对要素关系不确定下的决策问题,可为决策者提供更加丰富的决策场景。
2 基于改进DEMATEL的区间对偶犹豫模糊多属性决策方法
2.1 改进DEMATEL相关定义
2.2 决策步骤



3 实例分析
3.1 模型求解



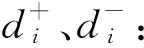
3.2 对比分析
4 结论
