考虑多禁止指向区域的航天器反步姿态机动控制
2020-09-14马广富柳明旻王靓玥郭延宁
马广富,柳明旻,2,王靓玥,郭延宁
(1. 哈尔滨工业大学控制科学与工程系,哈尔滨 150001; 2. 上海航天控制技术研究所,上海 200233)
0 引 言
随着航天技术的不断发展,航天器结构愈发复杂,航天任务愈加多样。执行科学任务的现代航天器装配了数量较大、造价昂贵的敏感元件,如星敏感器、红外望远镜、红外干涉仪等[1]。这些敏感元件容易受到强光强热天体的影响而失效,因此应考虑避免太阳光、地气光、甚至月光等杂散光进入视野。同样比如在在轨服务、空间攻防、碎片清除等空间任务中,还需要考虑目标对观测视野的遮挡或者反射等。综上各种因素以及其它约束的存在,导致了航天器在轨运行过程中存在某些禁止指向的姿态约束集。特别是在姿态机动过程中,为了确保该过程敏感器持续可用,必须在整个机动过程考虑禁止姿态指向约束集的情况下规划可行姿态机动路径及设计姿态控制律。需要注意的是,该禁止指向姿态约束集同航天器自身运动状态、敏感器视野、光源或者目标位置等因素均相关,使得约束条件难以给出适于控制系统设计的通用描述。此外,考虑规避多禁止指向区域的航天器可行姿态机动区域是一个无界非凸的空间,对于相应的控制系统设计带来了诸多难点。
近年来,各国学者针对考虑禁止指向区域的航天器姿态机动控制进行了广泛的研究,并取得了一定的进展。目前,可以将解决此问题的方法分为路径规划法和人工势函数法两类。
路径规划是指在空间中设计一条可以规避禁止指向区域的姿态机动路径,并施加跟踪控制力矩使得航天器沿此路径完成姿态机动。Singh等[2]针对Cassini号探测器设计约束监测法,并成功应用于Deep Space 1实际任务中,但该方法仅适用于某些特定任务自主姿态规划,不具有普适性。Spindler[3]、Hablani[4]通过分析敏感器指向和明亮天体方向之间的几何关系,在航天器机动操作前规划一条沿禁止指向区域切线的可行姿态机动路径,但其规划过程未考虑航天器动力学特性,计算复杂。Frazzoli等[5]、Kornfeld[6]应用如遗传算法等随机算法解决了禁止指向约束等多种不同约束的姿态机动规划问题,但其计算量受到约束种类、航天器姿态等多种因素的影响。Sun等[7]将禁止指向约束转化为二次型函数,并将姿态机动问题转化为二次型规划问题,利用提出的一种最小秩方法求解最佳的机动路径。但该方法计算量较大,需要多次计算获得最优解。缪远明等[8]将多约束条件下的姿态机动路径规划控制问题转化为最优化控制问题,并采用基于比例微分控制编码方法的粒子群优化算法进行求解以得到最佳的机动路径,但其需要进行多次迭代搜索,规划时间较长。路径规划方法通常可以获得最佳的机动路径,但其计算量较大、计算时间较长,故该方法更适用于离线或慢变的简单约束任务场景,不宜用于考虑多种复杂约束的实时在线航天器自主姿态机动任务。
势函数法最初应用于机器人在操作空间的路径规划问题,其具有结构简单,易于实时控制、计算简单的优点,目前已被应用于天体软着陆、飞行器编队飞行、航天器自主交会和路径规划等航天领域[9]。势函数法应用于规避禁止指向区域的航天器姿态机动也取得了一定的研究成果。McInnes[10-11]设计了基于高斯函数的人工势场函数以规避太阳光的照射,并将其引入李亚普诺夫函数中进行大角度姿态机动控制律的设计。然而由于其采用欧拉角描述航天器的姿态及其约束,可能导致姿态机动过程中存在奇异问题。郑重等[12]在此基础上采用四元数描述航天器的禁止姿态约束以及高斯人工势场函数,并分别对有无扰动下闭环系统的稳定性进行了分析。张景瑞等[13]基于禁止姿态作用范围设计一种可以规避局部极小值的势函数,并利用反步法对控制律进行设计。崔祜涛等[14]通过在单位球面上建立视线轴对应的导航函数设计了一种基于反步法的指向约束姿态机动控制律,并对控制律进行改进使其同时满足输入受限和常干扰抑制。Kim等[15]基于四元数描述方式对空间中多种姿态约束进行参数化凸描述,并利用凸优化方法对航天器的控制律进行设计。Lee等[1]利用该参数化约束描述设计了一种凸对数势函数,并分别根据李亚普诺夫直接法和改进反步法设计了模型独立及模型非独立两种姿态控制律。该方法能够满足多种姿态约束的同时在任意初始条件下保证系统的全局收敛性,但其设计的对数势函数缺乏较明确的物理意义。同时,Lee等[17]还应用此约束描述将问题转化为凸优化求解问题,并利用高斯伪谱法求解了考虑多种姿态约束下的时间能量最优控制。冯振欣等[18]针对微小卫星存在多重指向约束的姿态控制问题进行研究,在考虑微小卫星计算能力有限的情况下,提出了一种基于对数型势函数的航天器姿态机动控制律,并同时解决了角速度受限问题。
由于现有的势函数存在局部极小值问题或缺乏较为明确的物理意义,本文在构造通用的禁止指向区域凸约束集的基础上提出了一种新型具有明确物理意义的凸势函数,能够有效地避免传统势函数中的局部极小值问题。进一步地,考虑多个禁止指向区域,设计一种基于反步法的姿态控制律,以实现航天器的自主姿态机动。通过典型数值仿真校验了所设计控制算法的有效性。
1 航天器模型建立
本文以刚体航天器为研究对象,采用四元数描述航天器的姿态,根据刚体动量矩定理以及刚体复合运动关系建立航天器的动力学和运动学模型如式(1)、式(2)所示:
(1)
(2)
其中,

(3)
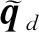
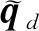
(4)
其中,
2 禁止姿态约束描述
航天器上装配有各类敏感器,在其姿态机动过程中,应避免太阳等光源进入敏感器视场,以保证敏感器的正常使用,将这类约束称为禁止指向区域。不失一般性,以太阳为例,其它光源的描述与其相同,其约束示意图如图1所示。其中,xi为航天器指向太阳方向的单位向量在惯性系的投影,y代表航天器敏感器视线方向的单位向量在本体系下的投影,θ代表该敏感器的视场大小。

图1 禁止姿态示意图
当航天器满足禁止指向约束时,光源未进入敏感器的视场范围,即代表方向的两个单位向量在同一坐标系下投影的夹角应大于敏感器的视场角,其数学表达式如式(5)所示:
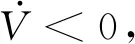
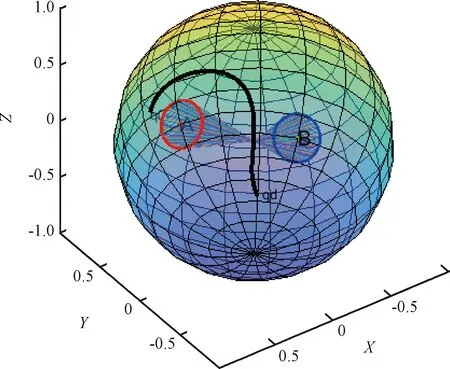
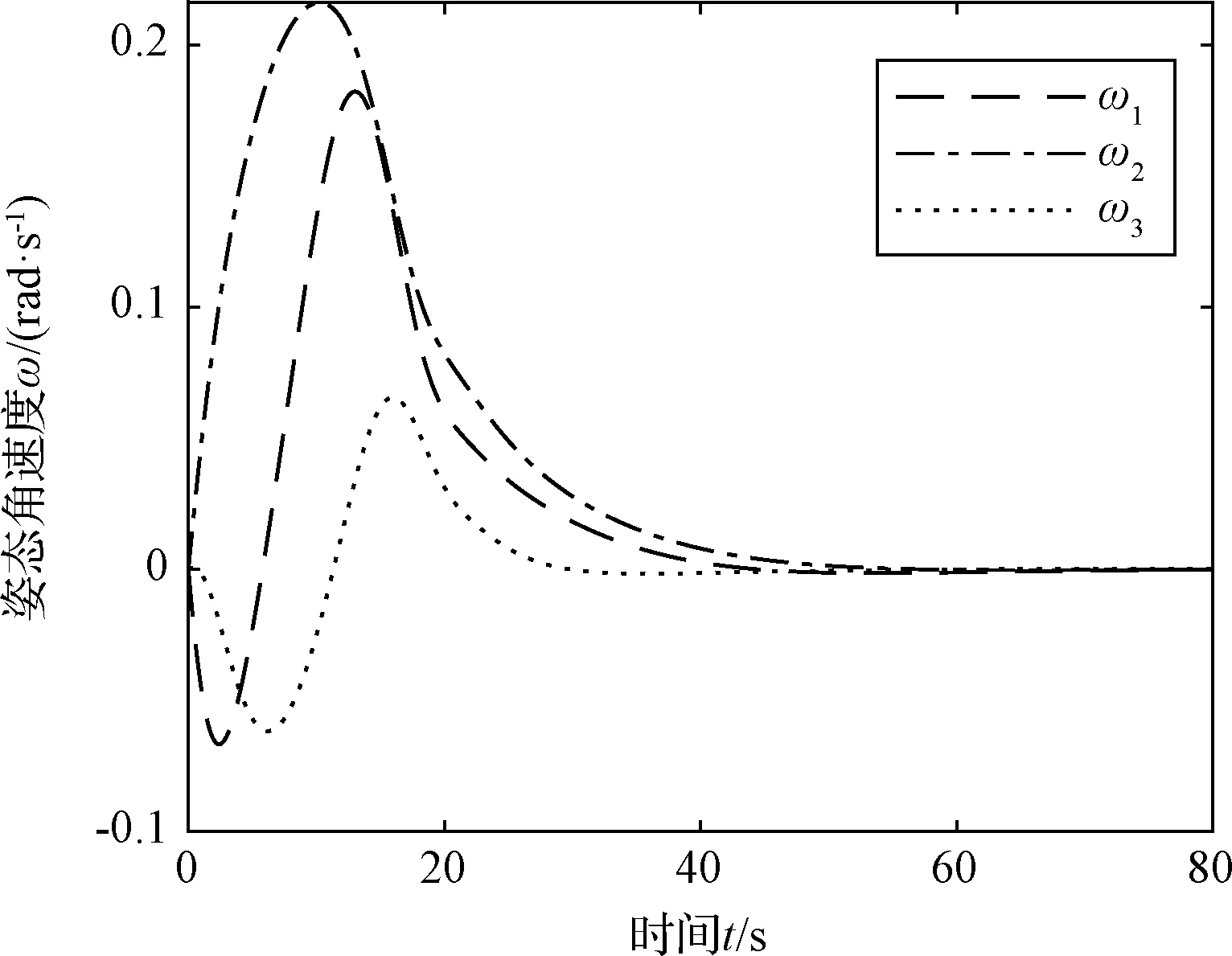
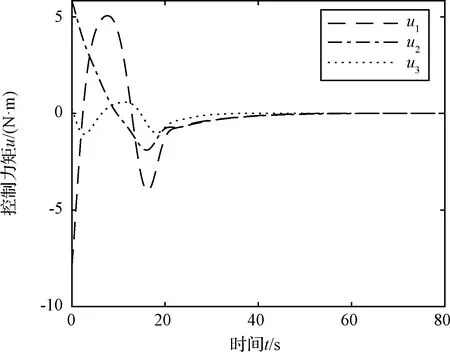
xi·yi (5) 式中:yi代表敏感器视线方向的单位向量在惯性系下的投影。 敏感器视线方向在惯性下的投影与航天器的姿态相关,实时变化,不能通用地描述禁止指向区域。因此,需要将敏感器视线方向在惯性系下的投影yi转化为其在本体系的投影y,转换关系如式(6)所示: 2(qTy)q+2q4(y×q) (6) 将式(6)代入式(5),并整理可得: 2qTyqTxi-qTq(xi)Ty+ (7) 对式(7)进行代数变化,转换为如式(8)所示的矩阵形式: (8) 其中,a=xiyT+y(xi)T-((xi)Ty+cosθ)I3,b=(xi)×y,d=(xi)Ty-cosθ 从矩阵A的定义可以看出,A为对称矩阵,其特征值均为实数。同时,由于A为非正定矩阵,式(8)描述的约束集为非凸集合。非凸约束集在寻找可行机动路径时不仅会增加计算的复杂性,而且会使姿态陷入局部极小值而不能到达期望姿态。因此,需要对该非凸约束集进行处理转化为凸约束集,并将约束中的姿态四元数转化为误差四元数的形式,为后续势函数以及控制律的设计提供基础。 定理1.禁止姿态约束集式(8)可以转化为如式(9)所示的凸约束集形式: (9) 证. 太空中的光源并非只有太阳,故应考虑姿态机动时存在多个禁止指向区域。实际航天器中敏感器分布在多个轴向,即航天器不止单轴受到禁止指向约束。但由于增加指向轴约束会使姿态机动的可行空间受到限制,求解复杂,故本文提出的控制律仅考虑航天器仅单轴受到多禁止指向约束,但延伸应用到多轴多禁止指向约束任务同样行之有效。 在第2节对约束集合凸化的基础上,本文提出一种新型的凸势函数,该势函数具有明确物理意义,且仅在期望姿态处具有全局极小值。考虑多禁止指向约束构建的势函数如式(10)所示: (10) 其中,ki>0为姿态禁止区域在势函数中代表的权重。此势函数中,分子代表了当前姿态与禁止指向区域的距离,距离越近,分子越小,产生的排斥力越大。而分母则描述期望姿态的吸引作用,姿态距离期望姿态越近,分母值越小,势函数的排斥作用越小。当航天器姿态到达期望姿态时,势函数值为0,即完成了姿态机动。 证. 下面证明该势函数是凸函数,通过对其海森矩阵(二阶梯度)的正负定性来判断其是否为凸函数,当其海森矩阵为正定矩阵时,该函数为凸函数。 该势函数的一阶梯度如式(11)所示: (11) 求导并整理得到二阶梯度如式(12)所示: (12) (13) 反步法是一种递归设计方法,其设计思想是递归地构造李亚普诺夫函数设计控制律,能够保证系统状态渐近收敛到平衡状态。式(1)、式(4)构成的航天器姿态误差模型是一个标准的级联系统[19],因此可以基于反步法对该系统的姿态机动控制律进行设计。 反步法控制律的设计分为两步。 第一步,设计虚拟角速度控制律使航天器的运动学分系统稳定。该分系统的李亚普诺夫函数即为式(10)所示的势函数,对其求取时间的全导数,如式(14)所示: (14) 式中:ωs为待设计的虚拟角速度控制律。 为保证该分系统渐近稳定地收敛到平衡状态,设计ωs如式(15)所示 (15) 式中:α>0为虚拟角速度控制律的设计参数。 此时,满足 在式(15)控制律作用下,该分系统渐渐稳定。 第二步,设计控制力矩使得虚拟角速度ωs趋近于真实角速度且渐近收敛于平衡状态,即使航天器的动力学分系统稳定。 定义虚拟状态量 (16) 构造李亚普诺夫函数为 (17) 对其求取时间的全导数可得: (18) (19) 为保证系统的渐近稳定性,设计控制律 (20) 将式(15)代入式(20)对控制律进行整理,得到利用反步法设计的基于势函数的航天器姿态控制律如式(21)所示: (21) 式(21)所设计的控制律由三项组成,其中第一项为航天器动力学非线性抵消项,第二项为虚拟角速度跟踪误差项,第三项为姿态误差控制项。在该控制律的作用下,航天器能够满足禁止指向约束的同时从任意初始状态机动到期望状态。 为校验该控制律的可行性对其进行数值仿真。本节考虑在空间中存在两个光源不能进入敏感器的视场,利用式(21)所示的控制律进行控制,验证其在完成姿态机动目的时能够满足姿态约束。 当航天器姿态误差较大或距离禁止指向区域较近时,由此控制律得到的控制力矩往往较大,虽然能够使航天器姿态快速机动到期望姿态及迅速远离禁止指向区域,但由于航天器的实际执行机构具有物理限制,因此需要考虑控制受限问题。通过合理选择控制律中各项参数,使得控制律满足幅值限制。 在航天器误差角速度有界的假设下,航天器的控制力矩幅值满足 (22) 具体的仿真条件如表1所示。 表1 仿真参数 本仿真算例中,控制力矩的幅值约束为10 Nm,选取控制律参数为α=0.54,β=30,搭建Matlab中的Simulink模型进行仿真,并绘制仿真结果图。航天器姿态机动过程中的误差四元数变化、误差角速度变化、控制力矩变化分别如图2、图3、图4所示。 为更直观地观察航天器姿态机动路径对禁止指向区域的规避,在三维球体上绘制出禁止指向区域以及航天器敏感器指向的机动路径图,如图5所示。 图5 航天器姿态机动轨迹三维示意图 其中,A锥体表示光源1的禁止指向区域,B锥体代表光源2的禁止指向区域。粗实线代表敏感器指向从初始姿态q0到期望姿态qd的机动路径。 从图2、图3可以看出,航天器误差四元数以及误差角速度的调节时间在60 s左右,系统的超调量和稳态误差范围合理。但由于控制律设计采用反步法,系统在到达平衡状态附近的控制作用较弱,趋向于平衡状态的时间较长。同时,图4中控制力矩的幅值始终小于10 N·m,满足饱和约束,但控制幅值受限带来了系统的调节时间较长的不利影响。 图2 航天器误差四元数仿真结果 图3 航天器误差角速度仿真结果 图4 航天器控制力矩变化图 从图5可以看出,航天器的姿态机动路径在靠近光源1或光源2的禁止指向区域时,由于受到势函数的排斥作用而偏离最佳机动路径,具体表现为在禁止指向区域附近的机动路径为远离该区域的两条弧线。这与控制力矩仿真图中出现两次尖峰相符合。同时禁止指向区域权重的大小不同以及距离期望姿态指向的远近不一,光源1产生的排斥力要强于光源2产生的排斥力,控制力矩仿真图4中表现为第一次尖峰的峰值大于第二次尖峰幅值,与仿真图5中弧线规避路径的半径大小不同相对应。 本文在结合物理意义明确的凸势函数基础上设计了一种基于反步法的航天器姿态机动控制律,能够快速稳定准确地完成航天器姿态机动过程的同时实现多禁止指向区域的规避。仿真结果表明了该算法的有效性。 未来将着手于航天器空间中受到禁止指向区域、强制指向区域等多种约束条件下的姿态机动控制,以及对目前控制方法进行改进加快稳态值附近的控制作用以获得更佳的控制效果。

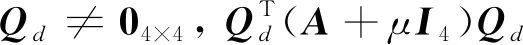
3 基于势函数的反步法控制律
3.1 势函数设计






3.2 基于反步法的航天器姿态机动控制律
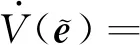

4 数值仿真



5 结 论
