静止轨道卫星远程交会策略设计

刘 涛，胡海霞，解永春，胡锦昌

(1. 北京控制工程研究所，北京 100094；2. 空间智能控制技术国家级重点试验室，北京 100094)

0 引 言

高轨道卫星尤其是静止轨道卫星，由于地面覆盖区域大，所以在通讯、遥感、数据中继、卫星导航等领域发挥着重要的作用。长寿命、高可靠性是高轨道卫星的重要特征，但受平台燃料携带量的制约，燃料耗尽已成为静止轨道卫星整体失效的主要原因[1]。此外，静止轨道的唯一性决定了静止轨道所能够容纳卫星的数量十分有限，故障失效的静止轨道卫星长期占用功能轨道，造成极大的资源浪费。通过发射在轨服务航天器，执行高轨道卫星在轨延寿以及故障卫星离轨操作，成为高轨道卫星技术发展的重要方向[2]，美欧等航天机构均积极开展了相关研究[3-5]。

高轨道在轨服务任务必须完成相对目标航天器的交会操作。交会过程可分为远程交会段和近程自主交会段两部分。远程交会段是指将追踪器从入轨初始轨道导引到近程自主交会段要求的预定轨道，并满足一定的相对运动约束的飞行阶段[6]。目前，人类所进行的交会对接主要集中在近地轨道，广泛使用的远程交会策略有两类：一类是特殊点变轨策略，即在远地点提升近地点高度，升交点修正轨道倾角等；另一类是综合变轨策略，即变轨点不局限于特殊点，同时修正轨道平面内外偏差[7]。虽然存在一定初始轨道面偏差时，综合变轨较特殊点变轨节省推进剂消耗，但是特殊点变轨的轨控位置较固定，物理意义更加明确，因此得到广泛的应用[8]。近地轨道多采用2～3天(飞行超过30圈)交会策略，例如中国SZ系列飞船的远程交会方案采用5脉冲轨控，持续时间约为28圈[9]。2～3天交会策略持续时间较长，给航天员和地面操控都造成较大压力。近年来，快速交会对接成为理论研究[10-11]和工程实践的热点，俄罗斯和中国均已成功实现了近地轨道6 h快速交会在轨飞行[12]。

目前，对静止轨道卫星远程交会的公开研究报道还比较少。梁斌等[13]提出在可实现相对测量的前提下，采用C-W方程，设计带制导精度约束和双视线夹角约束的分布式多脉冲优化制导，实现远程交会。孙振江[14]同样基于C-W方程，研究了静止轨道共位约束下多脉冲接近轨迹安全规划问题。Barbee等[15]采用共面椭圆交会策略设计了相距300 km以内的交会策略。Li等[16]采用多脉冲Hohmann轨控进行高轨道卫星远程交会相位调节策略设计。Yu等[17]基于混合最优控制理论研究了静止轨道空间碎片清理的优化调度问题。

对静止轨道在轨服务任务，由于轨道运行周期长(周期为24 h)，若沿用近地轨道2～3天交会策略(飞行超过30圈)，则远程交会过程过长，无法满足实际任务的时效性要求，因此有必要采用快速交会策略；此外，静止轨道半长轴超过40000 km，远程交会相对距离可达数千千米，很难建立相对测量，也不满足相对动力学方程(如C-W方程)的应用范围，采用基于绝对定轨的轨控策略设计远程交会方案更为适合。基于近圆偏差方程的变轨规划是综合变轨策略的经典方法，在近地轨道交会任务中得到成功应用[18]。本文将该方法应用于GEO卫星远程交会设计，并通过改进迭代制导求解中的制导误差求解方式，对传统基于近圆偏差方程的变轨规划策略进行改进，提高了制导精度。具体而言，本文针对高轨道卫星在轨服务任务，提出了一种4脉冲远程快速交会规划方法，可在5圈内完成远程交会过程。调相设计中，通过对传统基于近圆偏差方程的变轨规划策略进行改进，设计得到了3脉冲调相方案。首先，固定第1和第2调相脉冲执行位置，对3个调相脉冲的速度增量及第3调相脉冲的执行位置进行设计优化；再固定第1调相脉冲，对第2和第3调相脉冲的速度增量和执行位置进行再次优化。轨道面调整设计中，通过求解轨道面节线位置，采用单一法向脉冲进行轨道面修正。

1 近圆偏差相对动力学方程

设定一个参考圆轨道上运行的航天器(称为参考航天器，其轨道系为OEXrefYrefZref)。基于参考航天器轨道建立圆柱坐标系(见图1)：原点为地心OE，X轴指向为参考轨道升交点赤经，Z轴指向参考轨道角动量方向，Y轴与X轴和Z轴符合右手原则。在圆柱坐标系，采用极坐标描述航天器运动：r为航天器位置矢量rs在参考轨道面投影的模值；θ为X轴到航天器位置矢量在参考轨道面投影的幅角，逆时针为正；z为追踪器位置矢量在Z轴的投影。在圆柱坐标系中，航天器的轨道运动方程为[18]

图1 圆柱坐标系示意图

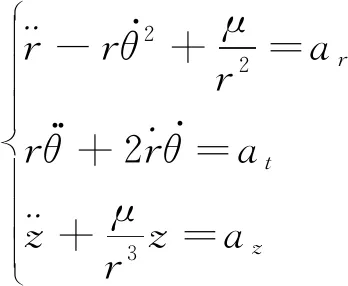
(1)

(2)

对应的t0和t时刻状态方程为：

X(t)=Φ(t,t0)X(t0)

(3)

式中：

(4)

Φv(t,t0)为Φ(t,t0)的4～6列，sα=sinα，cα=cosα，α=ωref(t-t0)为角距，ωref为参考航天器的轨道角速度。

2 远程交会轨控规划方法

基于近圆偏差相对动力学方程，通过设定不同的调相优化参数，李革非[18]给出了两类调相规划方程，并且给出了相应的迭代求解策略。该策略采用追踪器到达瞄准点同相位时刻构造切向位置差，其优势是算法收敛快，但是误差较大。本文在该收敛解的基础上，通过采用追踪器终端时刻的相对位置计算精确切向位置差用于再次迭代计算，以改进制导精度。以下首先介绍调相规划方程和基于近圆偏差方程的经典规划方法，再对改进后的变轨策略规划方法进行说明。

2.1 调相规划基本方程

1)面内3迹向脉冲及第3脉冲执行位置规划方程

设调相仅采用切向脉冲，且第1脉冲和第2脉冲分别在远地点和近地点执行(即第1和第2切向脉冲距离瞄准位置的角距α1和α2为已知)，规划变量为Δvt1，Δvt2，Δvt3，α3。采用近圆偏差相对方程进行规划[18]：

(5)

其中，

XA为瞄准点的状态，Xk为无控状态下的时间递推状态。

角距α3满足非线性方程

(6)

通过求解该非线性方程可以得到α3，进而可以得到各次脉冲为：

(7)

(8)

(9)

2)面内2迹向脉冲及执行位置规划方程

设调相仅采用切向脉冲，同时对脉冲增量和执行位置进行规划，规划变量为Δvt1，Δvt2，α1，α2。同样采用近圆偏差相对方程进行规划。

α1，α2满足以下非线性方程组：

(10)

通过求解以上非线性方程组得到α1，α2后，得到脉冲量

(11)

(12)

2.2 基于近圆偏差方程的变轨策略规划

采用第2.1节给出了两种不同规划方程，需要基于一定的规划策略得到最优收敛解。李革非[18]给出了一种基于近圆偏差方程的变轨策略规划，步骤如下所述。

步骤1：外推目标器轨道至瞄准点时刻tA，计算参考轨道和期望瞄准点间的相对状态XA。

步骤3：据δXk-1求解近圆偏差方程，转化为控制量。

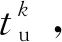
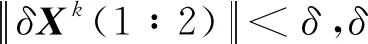
步骤6：赋值δXk=δXk-1+δXk，转步骤3(赋值k=k+1)。

2.3 改进的基于近圆偏差方程的变轨策略规划

基于近圆偏差方程的变轨策略规划中，步骤4采用时间差tA-tu，构造追踪器tA时刻位置与瞄准点间的切向位置差δX(2)=arefωref(tA-tu)，所得到切向相位位置差与真实值有一定误差，进而会影响制导精度。为此，本文在步骤4中通过采用追踪器终端时刻的相对位置计算精确切向位置差用于迭代计算，可改进制导精度。改进算法计算步骤如下所述。

步骤1：外推目标器轨道至瞄准点时刻tA，计算参考轨道和期望的瞄准点相对状态XA。

步骤3：依据δXk-1求解近圆偏差方程，转化为控制量。

步骤6：赋值δXk=δXk-1+δXk，转步骤3 (并置k=k+1)。

2.4 轨道面修正策略

(13)

(14)

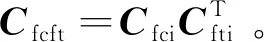
(15)

脉冲的执行位置(纬度幅角)u由lct确定。

3 远程交会轨控规划策略设计

设定在轨服务航天器在亚静止轨道进行巡航飞行，需要执行在轨服务任务时由地面/自主启动与静止轨道目标的交会流程。执行轨道机动前首先必须进行精确地面定轨，设定进行交会前进行1个轨道周期的轨道测定，交会流程从第2圈开始执行。远程交会采用3切向脉冲进行轨道面内调相，1法向脉冲进行轨道面修正。快速交会任务的远程交会规划方案如表1所示。

表1 远程导引轨控方案

远程交会轨控规划计算，共进行3次迭代优化，具体计算流程如下(图2为流程图)：

图2 远程交会制导规划流程

1)第1次迭代优化。设调相均采用切向修正，且Δvta1，Δvta3分别在第2圈远地点和第4圈近地点执行，采用基于近圆偏差方程的变轨策略规划方法(见第2.2节)，对迹向脉冲及第4脉冲的执行位置(距离瞄准点的角距)进行规划，结果记为Δvta1，Δv′ta3，Δv′ta4，α′4。

2)轨道面修正。根据脉冲Δvta1，采用精确轨道动力学进行外推。依据脉冲执行后的轨道参数，按照轨道面修正方法(见第2.4节)，计算得到vn2和对应的轨控位置u2(纬度幅角)。

3)第2次迭代优化。由于轨道面修正会对面内轨道参数造成影响，因此采用面外与面内解耦设计会带来误差。为此，根据脉冲Δvta1和vn2，采用精度动力学方程外推计算得到脉冲1和脉冲2执行后的轨道参数。采用基于近圆偏差方程的变轨策略规划方法(见第2.2节)，对脉冲3和4及其执行位置进行规划，结果记为Δv″ta3，Δv″ta4，α″3，α″4。

4)第3次迭代优化。为提高制导精度，继续采用改进的基于近圆偏差方程的变轨策略规划方法(见第2.3节)，根据脉冲Δvta1，vn2，u2，基于精确动力学方程外推计算得到脉冲1和脉冲2执行后的轨道参数，以Δv″ta3,Δv″ta4,α″3,α″4作为初始值，对脉冲3和4及其执行位置进行再次规划。结果记为Δvta3，Δvta4，α3，α4。

5)将轨控位置转换为对应圈次的纬度幅角，最终规划结果为Δvta1,Δvn2,u2,Δvta3,u3,Δvta4,u4。

4 仿真分析

设定目标航天器位于静止轨道，在轨服务航天器经地面导引已经进入低于目标器轨道400 km的漂移轨道。规划初始时刻为2019年10月14日05∶30∶0.00(BJT)，对应轨道圈次为1，以卫星经过升交点作为轨道圈次累加条件。轨道动力学采用20×20阶地球非球形摄动模型并考虑太阳和月球引力摄动，轨道控制采用脉冲方式实施。设定目标交会时间为tA=345600 s(4天)。远程交会的控制目标为：在tA时刻捕获瞄准点(目标器VVLH系中的相对位置和速度)XA=[-25km00000]T。两航天器的初始轨道参数见表2。

表2 初始轨道参数

4.1 远程导引轨控结果分析

到达初始瞄准点时刻tA时，服务航天器在目标器VVLH轨道系中的相对状态见表3，依据远程交会轨控方案计算得到的轨控参数见表4，飞行过程运动参数见图3～7。由仿真结果可知，初始瞄准点时刻时，相对位置控制误差优于100 m，速度控制误差优于0.01 m/s，精度满足转入近程自主交会的要求。轨控速度增量为20.1 m/s。

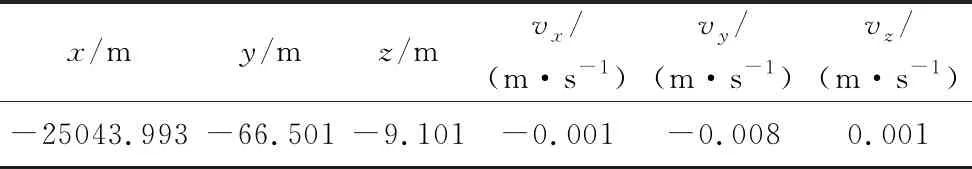
表3 瞄准点时刻的相对状态

表4 轨控执行位置和速度增量

图3 飞行过程的面内轨道参数

图4 飞行过程的轨道面参数

图5 轨道系相对运动轨迹(X-Z)

图6 轨道系相对运动轨迹(X-Y)

图7 轨道系相对运动速度

4.2 初始相位角差与速度增量变化分析

不同初始相位角差对总速度增量和各次轨控的速度增量有明显影响。为此，通过改变在轨服务航天器的初始真近点角，分析了不同初始相位差时的轨控速度增量，见图8和图9。由图8可知，初始相位差与总速度增量呈正相关。小于16°时总速度增量趋于恒定，初始相位差超过16°后，则总速度增量快速增大。这是由于初始相位角差较大时，为追赶相位需要降低轨道高度，从而造成先降轨再升轨的情况，增加了燃料消耗。由图9可知，随着初始相位的增大，第1次脉冲由升轨转变为降轨，而第4次脉冲则由降轨转变为升轨，第3脉冲的变化不大。这是由于初始相位大时保持较低的轨道高度更加有利于追赶相位，而在第4次轨控时才集中抬升轨道所致。实际工程设计中采用有限推力实施轨控，为保证远程交会精度，通常不希望最后一次轨控的速度增量过大而影响执行精度。为保证远程交会精度并确保燃料消耗最小，初始相位差应该限定在16°以内。

图8 不同初始相位差时的脉冲速度增量

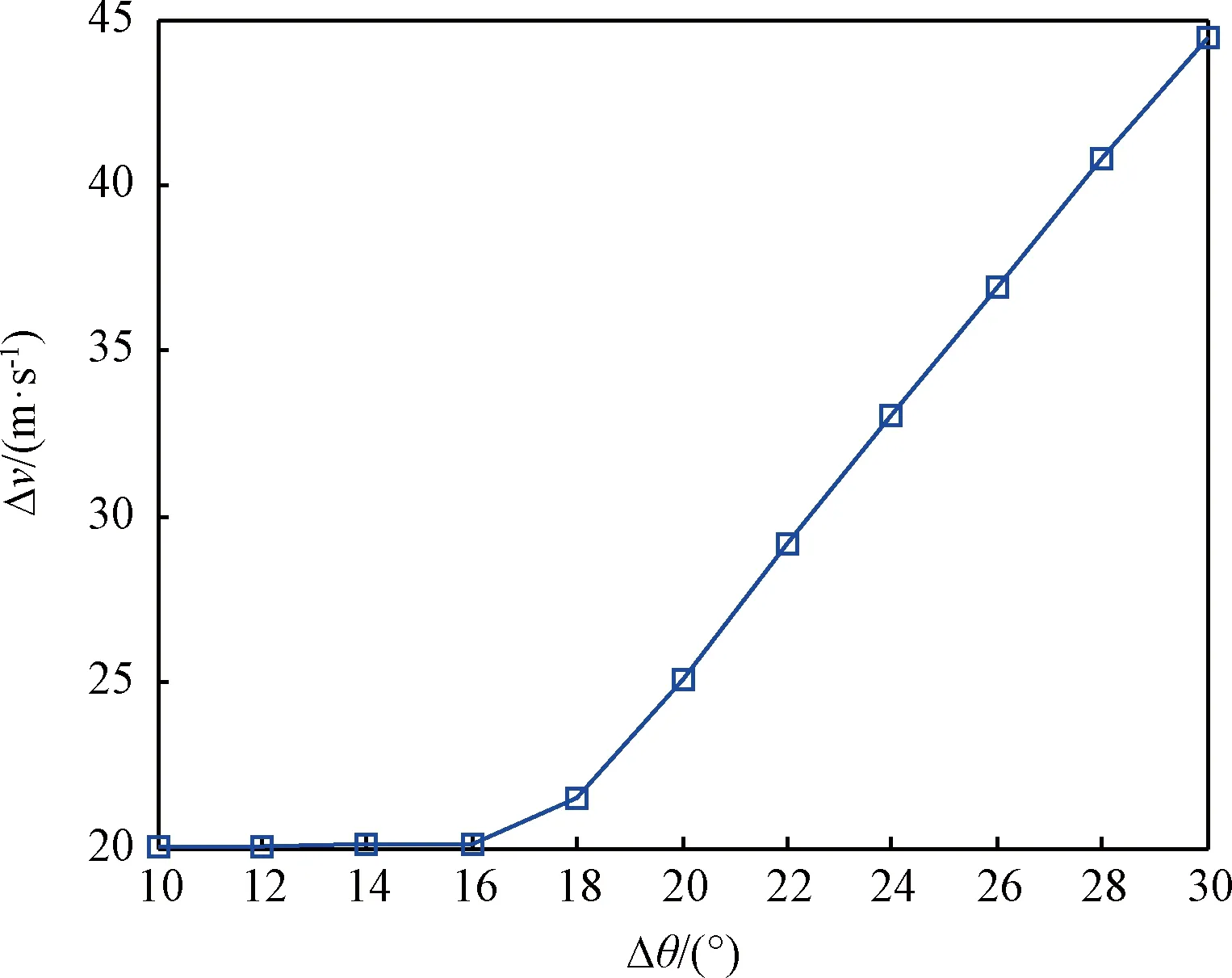
图9 不同初始相位差时的轨控总速度增量

5 结 论

论文针对静止轨道卫星在轨服务任务，对远程交会轨控规划方案进行了研究。采用近圆偏差方程的变轨策略规划，提出了一种4脉冲远程快速交会规划方案，可在5圈内实现远程交会。调相设计中，通过对传统基于近圆偏差方程的变轨规划策略进行改进，设计得到了3脉冲调相方案。轨道面调整设计中，通过求解轨道面节线位置，采用单一法向脉冲进行轨道面修正。所提出的方法可作为实施高轨道卫星快速交会任务的技术参考。