小学数学教学中学生数学建模过程探析

顾玮楠

摘  要：数学教师研究学生的数学建模过程，才真正地抓住了数学建模教学的关键。從模型建构的角度来看：将学生思维加工的素材变成大脑中清晰的表象，然后寻找到判断位置与方向的方法，才能够帮学生建立起模型认识。数学建模的认知过程是：首先是知觉启动，然后是图式激活，再然后是数学表征，最后是模型运用。教师只有从学生学习的角度去研究数学建模的过程，才能真正掌握数学建模的规律，发现学生在数学建模过程中可能会遇到哪些挑战，而有针对性地解决这些问题，也才能让教师的数学建模教学水平日益提升。

关键词：小学数学;数学建模;建模过程

数学建模在数学教学中的地位一直都是重要的，30多年前，义务教育各个学科曾经出版过一套关于建模的书籍，而事实上，关于数学建模的研究，在那之前早就开始了。直到今天数学学科核心素养的提出，数学建模依然在其中占有一席之地，而在数学教师的教学研究情境中，数学建模更是作为一个挂在口头上的概念而频频被提及。

什么是数学建模？数学建模就是运用数学的思想、方法和知识建立数学模型的过程。这是一个非常学术的表达，甚至因为过于学术化，而显得有些不接地气。相信多数一线教师是不喜欢这样的表达的，如果思考得更加深刻一些，还会发现其中存在着另外一个问题：如果说教师对数学建模的理解因为概念化、学术化而有些模糊的话，那么又如何真正认识到学生的建模过程是怎样的呢？要知道，作为一个数学教师，如果不知道学生的数学建模过程是怎样的，那么数学建模的教学就难免以己昏昏而使生昭昭了。因此笔者认为，数学教师研究学生的数学建模过程，才真正地抓住了数学建模教学的关键，小学数学教学中关于数学建模的研究成果，可以说是车载斗量，而将目光锁定在学生建模过程的研究并不多见，笔者不揣浅陋，决定做一个尝试。

一、小学数学建模理解：从宏观到微观

首先可以肯定的是，数学建模对于小学生的数学学习而言，意义是不言而喻的。将数学建模思想应用于小学数学教学过程，能较好地简化抽象数学知识的难度，有利于构建学生数学知识网络，树立学生信心，提升学生课堂参与度，从而提高教学效率。可以说这是一个比较公认的判断，但笔者仍然想强调，对小学数学建模的理解，仍然应该更细致一些，应当坚持从宏观到微观，只有体察入微，才能知道学生在数学建模过程中会经历了一些思考，会遇到哪些困难，教师的数学建模教学才能真正做到有的放矢。也就是说，教师在教学中引导学生建立数学模型，不仅要重视其结果，更要关注学生自主建立数学模型的过程，从而让学生在进行探究性学习的过程中科学地、合理地、有效地建立数学模型。

例如，在“位置与方向”的教学中，帮学生认识位置与方向，看起来是一个常识教学，实际上却是为了帮学生建立模型。有经验的小学教师都知道，相当一部分学生对位置与方向的判断是模糊的，不少学生甚至到小学毕业都难以迅速地判断东西南北，在让人啼笑皆非的同时，却又应当引发思考：位置与方向的教学，如何才能在数学建模的思路之下，更好地达成预期的效果。

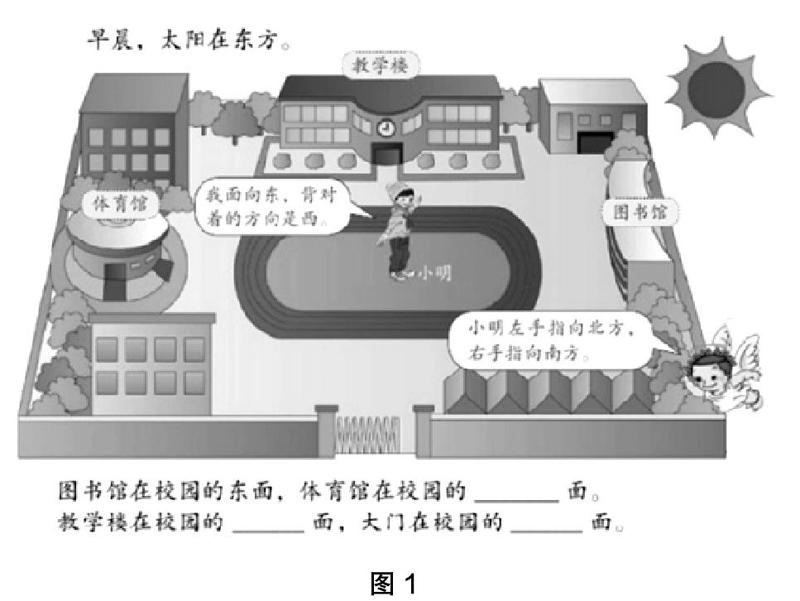
笔者的观点仍然是，要从微观的视角研究学生的数学建模过程。在“位置与方向”的教学中，教材给学生设计了一个具体的情境（如图1），然后让学生根据太阳的位置以及相关的说明，去判断一些建筑物的位置;实际教学中，可以将这一画面转换为学生的具体学习生活环境素材，如直接向学生提问：我们上课的教室在学校的哪个位置？学校大门在哪个方向？……

但是这样是否就能够帮学生建立起位置与方向的认识呢？笔者以为是值得商榷的。笔者研究过：对于这些问题的回答，回答正确的学生凭借的是经验，回答错误的学生缺少的是表象（也可以说是模型认识），因此只是这样的一问一答，是不足以培养学生的模型认识的。从模型建构的角度来看：将学生思维加工的素材变成大脑中清晰的表象，然后寻找到判断位置与方向的方法，才能够帮学生建立起模型认识。

二、小学数学建模过程：从现象到本质

基于以上分析，教师将研究的视角从宏观转向微观，那对数学建模的过程就要从现象转向本质。谈到本质，数学教师一般都知道，数学在本质上就是在不断的抽象、概括、模式化的过程中发展和丰富起来的。数学学习只有深入到“模型”“建模”的意义上，才是一种真正的数学学习。而从认知的角度去理解并设计数学建模的过程，显得非常必要。

同样以“位置与方向”的教学为例，基于数学建模的教学设计一般是这样的：

首先，创设情境，让学生判断位置与方向。这一步以上述第一点中的素材为情境素材，具体不赘述。

其次，数学体验，帮学生建立“位置与方向”表象。这一步主要是在学生已有经验的基础上，让学生通过画图的方法，去将自己对位置与方向的认识用图表示出来。这里涉及一些细节，比如画图时对“上北下南、左西右东”方向的确定，又比如将实际的位置转换为图上的位置，等等。画图实际上是一个输出的过程，也是让表象变得更加清晰的过程。

再次，数学应用，帮学生强化模型认识。这一步强调的是迁移，也就是让学生将自己对位置与方向的认识，运用到新的生活情境当中，比如让学生拓宽视野，画出上学一路标志性建筑的位置，等等。

如果说教学设计是现象角度，那么认知的角度就是本质。数学建模的认知解释是这样的：首先是知觉启动，然后是图式激活，再然后是数学表征，最后是模型运用。从这个视角去看上述教学设计：利用生活经验创设情境实际上就是为了启动学生的知觉;而建立表象实际上就是激活学生的图式，如果学生的图示不够完整，那么教师就要在教学中采用多种方式，如讲授或者学生之间的合作等;当图示完整之后，就要进行输出，这也就是数学表征，画图就是一种很好的表征方法，尤其适合小学生的数学建模，即使不是“位置与方向”这样的知识，很多时候也可以选择画图的方法;而最后数学应用的过程，首先是为了帮学生检验所建立起来的模型是否合理，实际上不少学生对上北下南、左西右东的规则比较抗拒，他们也确定了自己的表示方法，但是在交流的时候就出现了困难，于是对方向的约定俗成，就使得他们改变了原来的思路。

事实上，通过上述教学设计，小学生对位置与方向的确定就进入了同一个模式，自然运用的也就是同一种模型，这个过程如果得到适当程度的重复，学生对这个模型的理解与运用就会变得越来越熟练。

三、小学数学建模评价：从经验到解析

作为教学研究的一部分，对数学建模的评价，影响着教师对数学建模的认识。同样从学术语言的角度来看，数学建模的本质，在于它更突出地表现了原始问题的分析、假设、抽象的数学加工过程，数学工具、方法和模型的选择分析过程，模型的求解、验证、再分析、修改假设、再求解的过程，体现了学数学和用数学的关系。如果将这一学术判断转化为经验判断，可能更加符合小学一线教师的需要，只不过这种经验判断不应当是纯粹经验的，而应当是经验解析式的。

上述第二点提供的认知视角，实际上就是一种很好的解析工具，甚至可以认为认知视角下的数学建模评价，本身就是一种模型：知觉启动——图式激活——数学表征——模型运用，就是认知视角下数学建模模型的初步表述。在这个模型当中，每一个环节以及每一次转换都有着丰富的研究空间：小学生的知觉如何启动？知觉启动是否必然激活学生的图式？用怎样的数学语言去表征形成的图式？如果建立起来的模型不符合预期，那该怎么办？对这些问题的思考与回答，实际上就可以驱动教师去研究学生的数学建模过程，同时也就决定了数学建模教学的质量。

笔者在教学实践中，对数学建模评价的解析视角，实际上进行过多次比较，结果发现从认知视角去进行解析，要比从经验角度去解析可靠的多。当然，上述认知视角还显得比较笼统，其中的每一个环节与环节转换，还存在着丰富的研究细节，比如在图示激活环节，学生可能会在自己的知识与经验系统中进行多次搜索，这里有一个匹配与识别的过程，也非常值得研究。总的来说，教师只有从学生学习的角度去研究数学建模的过程，才能真正掌握数学建模的规律，发现学生在数学建模过程中可能会遇到哪些挑战，而有针对性地解决这些问题，也才能让教师的数学建模教学水平日益提升。