创设深度学习情境 培养数学核心素养

王思思 何棋

摘  要：以具体的心形曲线面积和位置问题为载体，类比用函数定积分求面积的方法，对极坐标曲线所围成图形的面积展开深度学习，利用GeoGebra软件动态展示极坐标曲线围成图形的面积的分割、近似、求和、取极限的形成过程. 通过综合分析与讨论，学生推导出极坐标曲线所围成图形的面积;再通过极坐标系中的极值和切线问题确定心形图形的大小和位置. 课后反思提出：设计适合的问题情境，促进深度学习落实数学学科核心素养;融合信息技术，培养数学学科核心素养;回归积分基本思想是“顺应”极坐标曲线围成图形的面积的求法的关键.

关键词：核心素养;深度学习;极坐标;面积与切线;信息技术

北京市海淀区2019年国际课程学术论坛暨第二届中外合作办学项目课程展示会在中国人民大学附属中学召开，研讨会关注的焦点是核心素养导向下的国际课程深度学习研究. 本文是展示课“极坐标曲线围成图形的面积与切线”教学反思. 展示课时长为1个小时，学生经历发现问题、提出问题、探索解决问题的工具和方法、应用工具和方法解决问题的过程，真实展示了学生在深度学习中发展数学学科核心素养的过程.

《普通高中数学课程标准（2017年版）》（以下简称《标准》）中提出了数学学科核心素养包括数学抽象、逻辑推理、数学建模、直观想象、数学运算与数据分析. 新一轮数学课程改革的核心任务是提升学生的数学学科核心素养，并要落实在教育教学的各个环节. 数学学科核心素养的形成是以数学知识为载体、以数学活动为路径而逐步实现的，情境化是数学知识转化为数学素养的重要途径. 教学过程中要“示以学生思维之道”：明确研究对象、研究目标，以及达到目标的思路概要，使学生学会思考，从而用数学的方式认识和解决问题. 本节课是AP美国国际课程微积分BC中的一节综合实践课，以“极坐标曲线围成图形的面积与切线”为例来谈谈如何基于问题情境培养学生的数学学科核心素养.

一、教学要素分析与设计

1. 教学内容

本章的主要内容是极坐标系下曲线和方程的相关问题，包括极坐标系与直角坐标系的转换，极坐标系下的曲线方程及其导数与积分的计算与相关应用等. 本节课是导数、积分、三角函数等内容的综合应用，主要通过实际问题抽象出数学问题，类比于直角坐标系下微积分的基本思想——分割、近似、求和、取极限，推导出极坐标曲线所围成图形的面积，进一步体会微积分的思想方法. 同时，将极坐标系转化为直角坐标系，利用导数求极值以及求曲线的切线来确定心形曲线的大小与位置，从而解决实际问题. 极坐标曲线围成图形的面积是用定积分解决几何问题的一个重要应用，同时也为之后解决极坐标系下弧长与表面积等问题打下了坚实的基础.

2. 教学目标

（1）能类比直角坐标系中函数图象与[x]轴所围成图形面积的探究过程，即分割、近似、求和、取极限，推导出极坐标曲线围成图形的面积公式，进一步体会微积分思想. 能利用导数求极值和切线方程，确定心形曲线的大小与位置.

（2）体会数学建模的过程与方法，发展数学抽象、直观想象、逻辑推理、数学运算等数学学科核心素养.

3. 学情分析

高二选修AP Calculus BC的学生具有很强的计算能力和逻辑推理能力，善于独立思考，也善于沟通交流和讨论. 内容上，他们已经能够深刻理解导数的概念，熟练掌握求导的方法，并能够应用导数求解相应的问题，也理解积分的概念，掌握积分的技巧，会利用定积分求曲线与[x]轴所围成的面积. 因此，设计涉及导数、积分、三角函数等内容的综合实践课. 希望学生能够从具体的实际问题出发，确定问题涉及的变量及其关系，并且进行数学抽象，建立数学模型，利用微积分的原理和方法进行求解或证明，最终解决实际问题.

4. 教学重点和难点

教学重点：如何将实际问题转化为数学问题;理解求极坐标曲线围成图形面积的思想方法及简单应用;会求极坐标曲线的切线方程与极值问题.

教学难点：对极坐标曲线围成图形的分割和近似;对极坐标曲线的切线相关问题中三角方程的求解.

5. 教学情境及策略设计

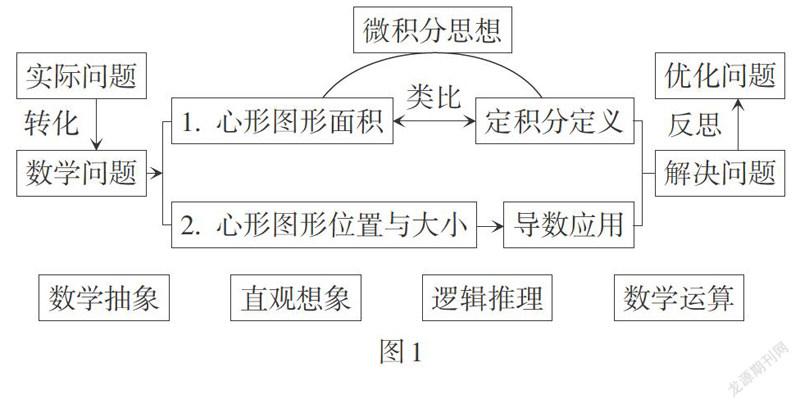
本节课为导数、积分、三角函数等内容的综合实践课. 引入实际问题情境，学生通过小组讨论抽象出两个核心数学问题：心形图形的面积，心形图形的位置和大小. 然后，通过微积分的思想方法，类比直角坐标系下微积分的基本思想——分割、近似、求和、取极限，推导出极坐标曲线所围成图形的面积，并通过数学软件展现其动态过程，加强了学生对微积分思想的理解. 同時，将极坐标系转化为直角坐标系，利用导数求极值和曲线的切线来确定心形曲线的大小与位置，从而解决实际问题，并反思优化问题. 在整个教学过程中，学生通过小组合作讨论的形式共同探索解决问题的方案，发展学生数学抽象、直观想象、逻辑推理、数学运算等数学学科核心素养，如图1所示.

二、教学片断

1. 问题导入及数学建模

我们已经学习了几类极坐标曲线，为了感谢老师对我们的谆谆教诲，宣传部计划制作感恩条幅，需要在[0.5×0.5 m]的正方形白纸板上画100个红色心形图案. 已知：1管21毫升的英国温莎牛顿染料大约能用[0.5 m2].

问题1：假设心形图案竖直放置在矩形白纸上，而且尽可能大，问大约需要多少管染料？

问题2：在正方形中，能否找到更大的心形曲线？

2. 问题1的解决过程

学生通过小组讨论将这个实际问题转化成两个核心的数学问题进行探究：心形图形面积的计算;心形曲线位置和大小的确定.

在教学过程中，学生通过实际问题情境进行数学抽象，充分利用所学知识，将其转化为数学模型解决问题. 以“情境”为主线来组织和调控起始课教学，能充分调动学生学习的主体性，培养学生的探究能力. 同时，小组成员合作评价，培养学生的数学思维能力. 此过程中，培养了学生用数学眼光观察世界，发展了学生的数学抽象、直观想象和数学建模等素养.

（1）针对心形图形面积的计算.

师：回顾一下，在直角坐标系中如何求曲线与[x]轴所围成图形的面积？

生1：对函数求定积分可得面积.

师：对心形曲线[rθ=1-sinθ]能不能这样做呢？

生2：可以.

生3：不可以，因为原来的函数是在直角坐标系下，求面积是对自变量[x]求定积分，而现在是在极坐标系下，自变量是[θ]，意义不同，因此直接这样求定积分应该是有问题的.

师：非常好！既然不能直接用，那我们能不能利用积分的基本思想方法来解决呢？用定积分求面积的基本思想方法是什么？

生4：通过分割（Partition）、近似（Approximate）、求和（Sum Up）、取极限（Find the limit）四个步骤求面积.

师：通过小组讨论的方式，详细分析如何进行分割、近似、求和、取极限.

生5类比直角坐标系得到如下步骤.

第一，分割极角（Directed Angle）.

第二，用扇形面积或者三角形面积近似，扇形面积[Si=12ri2Δθi]，三角形面积[Si=12ri2sinΔθi].

第三，求和[i=1nSi].

第四，取极限[limn→+∞i=1nSi=αβ12r2θdθ].

利用图形计算器的轨迹功能，可以得到角度的范围为[0，2π].

接下来，教师结合GeoGebra软件动态展示形成过程，如图2和图3所示.

此时，选取[θ=270°]，[Sn′]表示以分割小角为扇形边长近似，[Sn″]表示以分割中点为扇形边长近似，[Sn？]表示以分割大角为扇形边长近似. 图中为[n=16]和[n=100]时三种近似与实际面积的对比情况.

教师通过类比对照直角坐标系和极坐标曲线围成图形面积的形成过程，在黑板上进行板书.

师：在[θ∈0，2π]时，心形曲线[rθ=1-sinθ]围成图形的面积是多少？

生6给出解答过程如下.

[02π121-sinθ2dθ  ]

[=1202π1-2sinθ+sin2θdθ                 ]

[=1202π1-2sinθ+1-cos2θ2dθ]

[=1232θ+2cosθ-14sin2θ2π0]

[=1232 · 2π+2-2]

[=32π].

教師最终总结呈现定理内容，强调被积函数的条件，以及角的范围.

（2）针对心形曲线位置和大小的确定.

学生在最初讨论中，考虑心形曲线竖直放置最大情况，就需要解决心形曲线是竖直相切还是水平相切. 那么，就转化成先计算基本图形[rθ=1-sinθ]的水平和竖直距离，至于心形图形的大小再等比例缩放即可.

师：针对心形图形[rθ=1-sinθ]，如何计算水平和竖直距离？满足什么条件？

生7：首先，将极坐标转化为直角坐标;然后，计算水平距离，即计算[x]轴方向的极值，通过[dxdθ=0]计算求解;计算竖直距离，即计算[y]轴方向的极值，通过[dydθ=0]计算求解.

生7的具体过程如下.

将其转化为直角坐标[x=1-sinθcosθ，y=1-sinθsinθ.]

求[x]轴方向的极值，令[dxdθ=2sin2θ-sinθ-1=0]，

得[θ=11π6]（极值点），[θ=7π6]（极值点），或[θ=π2]（非极值点）.

所以[xmax=334].

则水平距离为[332]，近似值为2.598.

求[y]轴方向的极值，令[dydθ=cosθ1-2sinθ=0].

得[θ=π2]（非极值点），[θ=3π2]（极小值点），[θ=π6]（极大值点）或[θ=5π6]（极大值点）.

所以[ymin=-2，ymax=14].

所以竖直距离为2.25.

因此，正方形的边长以水平距离为标准.

师：在[0.5×0.5 m2]的正方形内，心形图形是怎样的？

生8：在[0.5×0.5 m2]的正方形内，心形图形曲线为[rθ=a1-sinθ]. 利用比例关系确定参数[a]，由[3321=][0.5a]，得 [a=39]. 因此在[0.5×0.5 m2]的正方形内，心形图形为[rθ=391-sinθ].

师：[0.5×0.5 m2]的正方形内的心形图形的面积是多少？需要多少管染料？

生9给出[0.5×0.5 m2]的正方形内的心形图形的面积：[02π12a1-sinθ2dθ=a202π121-sinθ2dθ=392 · 32π=][π18]（[m2]）. 因此，通过计算，需要约35管染料.

首先，在这部分的教学过程中，利用类比方法，通过分割、近似、求和、取极限的具体过程，学生推导出计算极坐标曲线所围成图形面积的过程，同时，教师在课堂上熟练巧妙地使用画图软件展现其动态过程，学生可以进一步体会微积分的思想方法. 其次，学生通过逻辑推理与运算求解，利用导数求极值的方法，计算心形曲线的水平距离和竖直距离，从而确定心形图形的大小与位置. 最后，通过运算解决实际问题. 这个过程培养了学生用数学的思维分析世界的能力，发展了他们的逻辑推理、数学运算等素养.

3. 问题2的解决过程

师：在正方形中，能否找到更大的心形曲线？

生10：由于图形的对称性，可以倾斜放置心形，如图4所示.

师：如何说明这个心形更大？

生11：针对正方形内的心形图形[rθ=1-sinθ]，只需要计算外接正方形的边长. 与水平距离比较，如果更小，那么说明这个心形图形更大. 由于对称性，将正方形的边长转化成计算两条斜率为1（或者-1）的平行切线之间的距离即可.

生11的具体求解过程如下.

因为曲线[r=1-sinθ]上的任意一点的直角坐标为[x=1-sinθcosθ，y=1-sinθsinθ，]

所以由参数方程的求导公式，得

[dydx=dydθdxdθ=-2sinθcosθ+cosθ-cos2θ-sinθ+sin2θ=1.]

整理，得

[sin2θ-cos2θ+2sinθcosθ-cosθ-sinθ=0，sin2θ+cos2θ=1.]

相加，得2[cos2θ+cosθ-1=2cosθ-1sinθ]，

即[2cosθ-1cosθ-sinθ+1=0].

解得[cosθ=12]，或[sinθ-cosθ=2sinθ-π4=1.]

解得[sinθ=32，cosθ=12] 或[sinθ=-32，cosθ=12] 或[sinθ=0，cosθ=-1] 或[sinθ=1，cosθ=0.]

检验：将[sinθ=1，cosθ=0] 代回[dydx]，分子分母为0，舍去.

根据点的坐标，得到切线的方程为[l1：y=x-][121+32-321+32]，即[y=x-54-334]，和[l2：y=][x+1].

则平行直线的距离为[-334-942=323+38≈2.510].

因为切线的斜率是1，所以将心形曲线的对称轴与正方形对角线重合放置心形曲线更大.

通过引导学生参与改变心形图形的位置的探索活动，逐步使他们认识到心形曲线应该与正方形相切，从而将最大曲线位置转化为求曲线平行切线的距离的最大值问题. 然后通过极坐标转化为直角坐标，通过推导dy/dx来计算切线斜率，从而求出切线，得到较大的正方形边長，体现了对导数概念的理解和应用，培养了学生的直观想象、逻辑推理、数学运算等数学学科核心素养.

三、教学反思

1. 设计适合的问题情境，促进深度学习，落实数学学科核心素养

相对于浅层机械学习，深度学习是一种基于理解的学习，它有三个特点：深度学习是有意义的学习，它不是单纯的接受，而是在发现基础上的同化;深度学习是基于深度理解的学习，它强调深度体验、深度思考、深度探究、深度整合，发现问题的本质，达成对学科本质和知识意义的深度理解;深度学习是批判与质疑的高阶思维学习，它强调了学习阶梯性和思维进阶性，强调了知识的普遍联系与综合应用. 本节综合实践课，从一个实际问题出发，循序渐进地引导学生开展深度学习，不仅是对导数、积分、三角函数的综合复习与应用，也是学生在解决问题的过程中深度体验实际问题数学化的过程，深度思考解决核心数学问题的方法，深度探究更优方案，突出培养了学生的数学学科核心素养.

培养学生数学学科核心素养要从选择“好问题”开始，在经历“感知感悟—知识建构”的过程中，注重过程思维，理解数学本质，寻找可行方法，从而解决实际问题. 通过数学抽象，学生将这个实际问题的情境转化为数学模型来解决，这也是培养学生深度体验与深度思考的过程. 以“情境”为主线来创设合理的教学情境，可以充分调动学生学习的主体性，鼓励学生去思考探究，激发学生提出核心问题. 本节课将红心染料的实际问题，通过竖直放置的假设后，转化为求心形图形的面积、心形图形的大小与位置两个核心问题. 显然这两个问题也并不简单，于是再将核心问题转化为具体可解的子问题，形成具有逻辑关系的问题链，有利于学生深度思考和深度探究. 在思考与提出问题的过程中，学生可以通过小组成员之间的合作、讨论、评价，真实地展现他们的数学思维过程，促进了学生用数学眼光观察世界，落实了对数学抽象、直观想象和数学建模等素养的培养.

在解决心形图形面积、极值问题、优化后切线问题的过程中，融入了深度学习的设计思想，在落实数学学科核心素养的同时，更让学生拥有了深刻的思维品质和持久的学习力，并在深度学习的过程中培养了学生批判与质疑的高阶思维能力. 具体地说，心形图形面积的计算是本节课的一个重点和难点，这个过程也是培养学生深度思考和深入探究的学习过程. 课堂上采用从特殊到一般的数学方法，先分析特殊情况下的心形图形[rθ=1-sinθ]的面积求解. 于是，类比直角坐标系下微积分的基本思想——分割、近似、求和、取极限，思考极坐标曲线所围成图形的面积计算. 针对有思维深度的新问题，通过苏格拉底提问的方式，引导学生进一步体会微积分的思想方法，并大胆尝试猜想极坐标系中如何进行分割、近似、求和、取极限的过程，并最终得出极坐标曲线围成图形的面积计算方法. 在积极探索、反思、总结、创造的过程中，学生把握了知识间的联系和解决问题的思想方法，并通过知识迁移应用到新的问题之中，这体现了深度学习所强调的学习阶梯性与思维进阶性. 此外，针对心形图形的大小与位置问题，学生则将其转化为导数求极值的问题. 极坐标切线方程的计算也是本节课的一个重点，要求学生对导数的本质与几何意义有十分深刻的认识，这也是深度学习中要注重的综合应用. 另外，类比直角坐标系中的定积分问题，学生在课后可以探究极坐标系下弧长和表面积的计算问题，为学有余力的学生打开深度学习的大门，促进他们实践能力和创新意识的发展，从而更好地感悟数学的科学价值与应用价值，并培养学生自主参与到深度探究中，完成对数学本质和知识意义的深度理解.

2. 融合信息技术，培养数学学科核心素养

《标准》指出，要充分考虑信息技术对数学学习内容和方式的影响，把现代信息技术作为学生学习数学和解决数学问题的强有力工具. 在数学课堂上，适当使用软件辅助数学教学，可以将无形化有形，直观形象地展现知识形成的过程，增强学生对知识本质的理解. 本节课中，利用微积分思想，类比直角坐标系中曲线与[x]轴围成图形的面积的计算过程，推导极坐标曲线围成图形面积的计算公式. 为了论证学生的猜想，教师在课堂上使用GeoGebra软件进行有限段的分割、近似、求和，通过计算功能与动画演示，学生可以具体、直观地体验图形无限逼近真实图形的动态过程，在面积数值上也可以观察到逼近极限的过程. 此外，对于三种近似方法也可以纵向对比，随着分割数目的增加，最终都会趋近于统一的极限值. 总之，信息技术软件不仅可以帮助学生将抽象的数学概念与数学方法直观化，检验他们的逻辑推理与数学运算，也可以培养学生的直观想象和数学抽象素养，激发学生自主探究、合作学习的热情.

3. 回归积分基本思想是“顺应”极坐标曲线围成图形面积的求法的关键，更是体现数学学科核心素养的载体

在求极坐标系中心形面积的过程中，学生课上很快提出像直角坐标系一样，直接求定积分就可以求面积，试图用函数求定积分求面积的方法来“同化”求极坐标曲线围成图形的面积. 在教师的启发引导下，通过回顾直角坐标系中曲线与[x]轴围成图形面积的求解过程，学生将分割、近似、求和、取极限平行到极坐标系中的具体过程，将极坐标曲线当作一般的直角坐标函数求定积分，通过数学软件画图验证了直接求定积分求得的面积与心形面积不一致，学生认识到存在的错误. 表明原来通过函数求定积分求面积不能“同化”极坐标曲线围成图形的面积的求法，需要寻求新的方法来“顺应”极坐标曲线围成图形的面积的求法. 但是这两者都是求面积，既然不能直接迁移，那就回归到积分基本思想来分析和判断，最终得出新的方法. 这样的不断猜想与验证、改进和论证，往往是培养学生数学思维的关键，不仅使学生对微积分思想有更加深刻的理解，还培养了学生的直观想象、邏辑推理、数学运算等素养. 此外，小组讨论探究的过程，激发了学生对数学学习的浓厚兴趣，培养了学生敢于探究、勇于实践、善于合作的科研热情.

总之，在数学深度学习活动中，要将知识作为教学的载体，借助问题的转化，数学问题的发生、发现等过程，有目的、有步骤地引导学生体验和感悟知识中蕴涵的数学思想和研究方法，引导学生思考、理解和应用，从而培养学生的数学学科核心素养，提高学生解决实际问题的能力. 教师应该更加关注如何引导学生在深度学习中提出问题和发现问题、分析问题和解决问题，教师要促进学生学会学习，这是数学学科核心素养形成的有效途径. 此外，教学过程中创设合适的情境，有利于激发学生的学习兴趣，并学会用数学眼光观察、分析世界，感悟数学的魅力，发现数学之美.

参考文献：

[1]核心素养研究课题组. 中国学生发展核心素养[J]. 中国教育学刊，2016（10）：1-3.

[2]中华人民共和国教育部制定. 普通高中数学 课程标准（2017年版）[M]. 北京：人民教育出社，2018.

[3]章建跃. 核心素养统领下的数学教育变革[J]. 数学通报，2017，56（4）：1-4.

[4]张金良. 构建深度学习课堂促进数学核心素养的养成[J]. 中学教研（数学），2019（11）：1-5.

收稿日期：2020-07-14

作者简介：王思思（1989— ），女，中学一级教师，海淀区骨干教师，主要从事高中国际数学课程教育和比较研究. 何棋系本文通讯作者.