不同震源参数下的围岩PGV分布规律及预测研究
2020-09-10王玺李施庆李秋涛程力刘焕新
王玺 李施庆 李秋涛 程力 刘焕新






摘要:为全面了解不同震源机制下地震波传播和分布规律及其对巷道围岩的影响,基于现场监测数据研究了不同震源参数下PGV的分布规律。研究结果表明,震源距离、矩震级及断层滑移角都会对PGV的分布产生不同程度的影响。通过比较经验公式计算PGV值与实测值间的拟合相关系数,判断各预测方法适用性。研究发现Sadov预测公式对爆破事件的PGV预测值与实测结果相关度更高。依据研究结果,计算了动态震源机制下PGV空间分布,并依此给出了不同震源位置和震级条件下的围岩支护建议。
关键词:金属矿山;震源;震动监测;PGV;预测公式;拟合相关系数
中图分类号:TD853.34文章编号:1001-1277(2020)10-0029-08
文献标志码:Adoi:10.11792/hj20201006
引 言
随着地表浅部资源的开采殆尽,金属矿开采开始转向深部。而由于地下金属矿复杂的开采技术条件及多变的矿岩受力状态,其采场内围岩会产生不同程度的开采扰动,同时也导致地下金属矿采场中存在多种高危的安全隐患[1]。在地下金属矿开采过程中,若对矿山井下强扰动的影响范围、具體位置、能量大小等缺乏准确的了解和认知,矿山工人与生产设备将持续处于极其危险且频率高发的灾害威胁中,并有可能引发重大的财产损失与人员伤亡,最终带来难以估量的损失。
在矿山震动的研究工作中,预测震动强度对震动安全的判据有着重要意义。震动强度(I)的预测方法依据表征震动强度物理量的不同而对应不同的形式,通常各类预测方法都符合以下函数形式[2]:
I=f(m,n,k)(1)
式中:m为震源;n为传播途径;k为仪器特性。
通过公式(1)发现,影响震动强度的因素多样且复杂,在计算过程中需要对多因素的影响进行综合考量[3-4]。由于通过多变量确认函数形式的难度很高,该过程一般会选择某些独立变量作为常数,在此基础上对其他变量进行研究,找到它们之间存在的函数关系。运用公式(1)及现场监测所得的震动相关数据能够对质点峰值震速、加速度、位移等参数进行预测,再由预测结果对震动强度进行评判。实际工作中运用最广泛的是对PGV(Peak Ground Velocity,PGV)进行预测。但是,在运用PGV经验公式对实测数据进行回归分析时,计算得出的回归系数离散性往往较大。所以经验公式在实际运用时会出现较多问题和局限性。为此,研究者结合现有经验将公式进行变形,得出了很多适用于各类情况的相关公式。例如:陈寿如等[5]在计算露天矿爆破产生的震动模型时加入了高差这一变量,得到了新的变形公式;韩子荣[6]基于对主频与结构自震频率影响的考虑得出了折合速度公式。在预测PGV时除运用传统线性回归方法以外,近些年研究者研发出了不少新的预测方法,比较典型的有:王民寿等[7]通过对双随机变量进行回归分析来预测震速;徐全军等[8-9]通过神经网络对震动峰值进行预测;黄光球等[10]通过遗传规划法对震动峰值进行预测。
综合上述研究,针对震动事件产生的应力波,采矿中经常使用PGV描述围岩在应力波作用下的能量平衡状态(能量需求与能量吸收能力)和动态变化,由此对围岩的稳定性和完整性作出评估[11]。因此,本次研究基于现场震动监测数据,对矿震数据在震源参数影响下的分布特征进行研究;并选取某矿震事件的震源参数,运用国内外已有的PGV计算公式进行预测计算;通过研究计算结果与实测值间的拟合相关系数,判断不同的计算公式在该事件PGV预测的适用性;最后运用优选计算公式的预测结果给出岩体支护建议。
1 围岩震动测定与分析
1.1 震源参数与PGV测定
山东金洲矿业集团有限公司金青顶矿区(下称“金青顶矿区”)坐落在黄垒河南岸的金青顶上,位于山东省乳山市下初镇。金青顶矿区整体属于硬岩矿山,最大开采深度已超过1 000 m,大部分采场和巷道布置集中、开挖空间较小,且众多采场与井巷工程的开挖空间结构参数和围岩性质不尽相同,这些因素导致该矿区的震动事件错综复杂,严重影响矿区范围内矿震监测和分析工作。
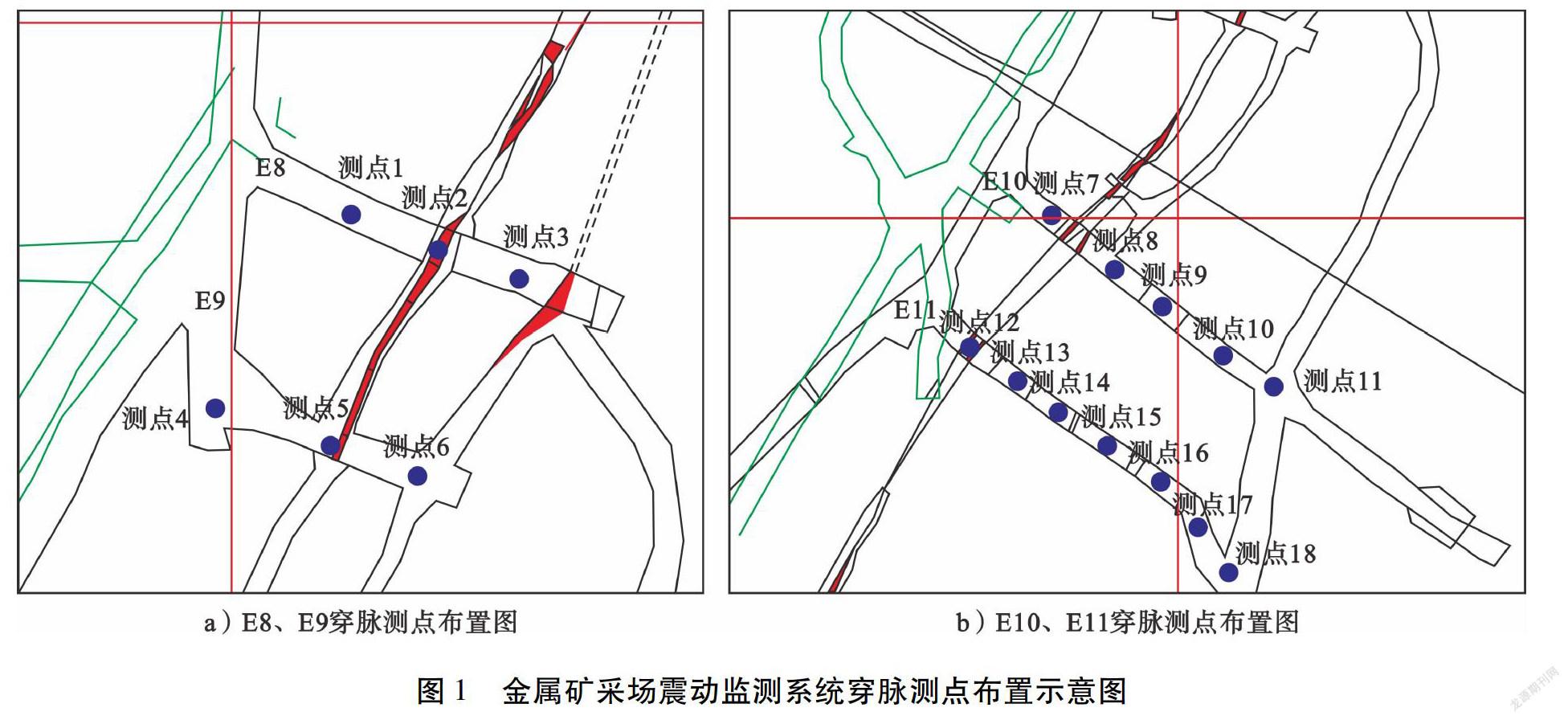
为解决该问题,需要对PGV在各项震源参数下的分布情况进行研究。利用局域微震监测系统(见图1)对该矿区-1 145 m中段E8、E9、E10及E11穿脉内的活动事件进行了跟踪记录,记录信息包括事件时间、矩震级、实测PGV、传感器距震源距离及相对位置等参数。将记录的监测数据与震源特征参数绘制成图,即可得到PGV与相关震源参数的关系图。本文分别讨论了震源距离、矩震级及断层滑移角对PGV分布的影响情况。
1.2 震源参数对PGV分布影响
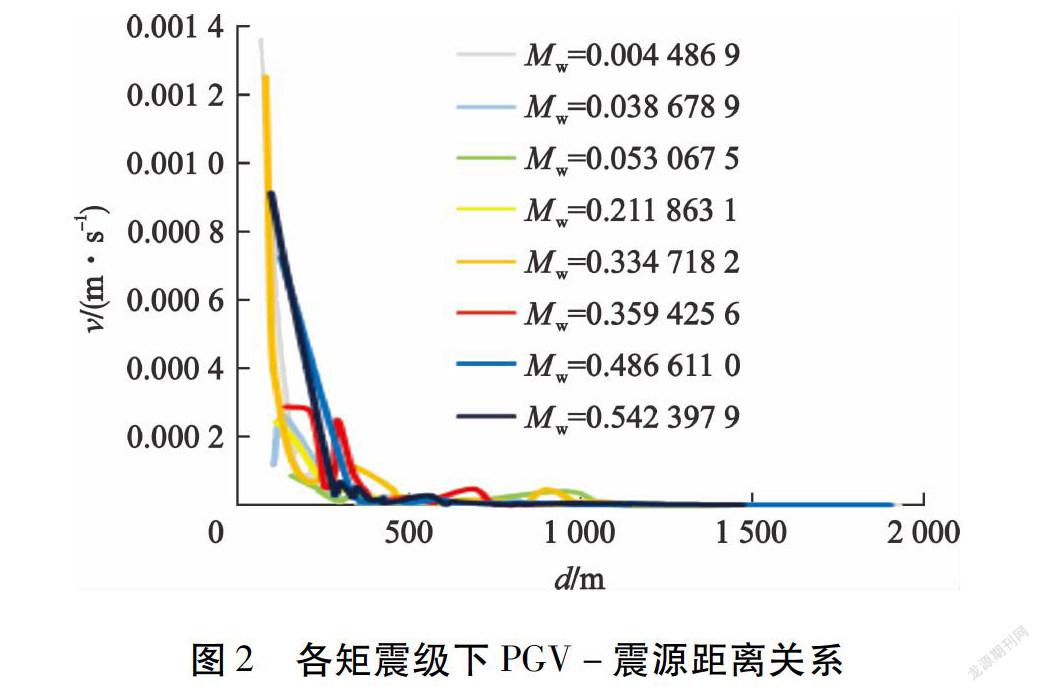
1)震源距离对PGV的影响。随机抽取8次震级不一的事件,绘制不同矩震级(Mw)下震源距离(d)与PGV(v)的关系,见图2。
从图2可以看出:随着震源距离的增大,震动的峰值速度都呈指数型下降趋势,说明传播过程中,岩石介质将对PGV产生明显的削弱作用。此外,PGV的衰减程度与震源距离也有着密切的联系,当震源距离d<300 m时,事件8(Mw=0.542 397 9)PGV随震源距离的衰减率为k1=4.776 784×10-6;当300 m≤d≤500 m时,衰减率k2=2.772 07×10-7;当d>500 m时,衰减率k3=5.883 29×10-8。由此可见,整体上PGV在传播过程中的衰减作用受震源距离的影响,在距震源距离较小时,震源距离对PGV的衰减影响较大;随着震源距离增大,PGV的衰减受震源距离的影响作用逐渐弱化。
2)矩震级对PGV的影响。矩震级是利用地震矩的大小确定震级,它由地震断层的破裂面积、平均错动量及岩石剪切模量的乘积来确定,是一个描述震动发生时力学强度的物理量。基于监测数据,取震源距离为100~200 m、200~300 m、300~400 m、400~500 m及500 m以上的5种情况下矩震级和PGV数值,分别绘制PGV(v)相对于矩震级(Mw)大小的散点分布图,见图3。
从图3可以看出:矩震级增大时,PGV值高的散点数量增多,整体上PGV呈现增大趋势;分析发现其原因可能是,随着矩震级的增大,断层的长度等尺寸参数变大,使得PGV随矩震级增大也显著变大[12]。但是,由PGV-Mw变化趋势公式(见表1)可知:在不同震源距离下,PGV随矩震级增大的程度有所差异,在近震源情况下,PGV受矩震级影响较大,随矩震级呈近指数趋势增长;但当监测点逐渐远离震源时,PGV受矩震级的影响减小,增大趋势逐渐减弱。由此说明,矩震级对PGV的分布有较大影响,且该作用效果随震源距离的由近至远逐渐衰减。
3)断层滑移角对PGV的影响。在金属矿山中,断层滑移角通常指矿体上下盘相对运动的方向(断层滑移方向)与断层的走向之间的夹角。为探究不
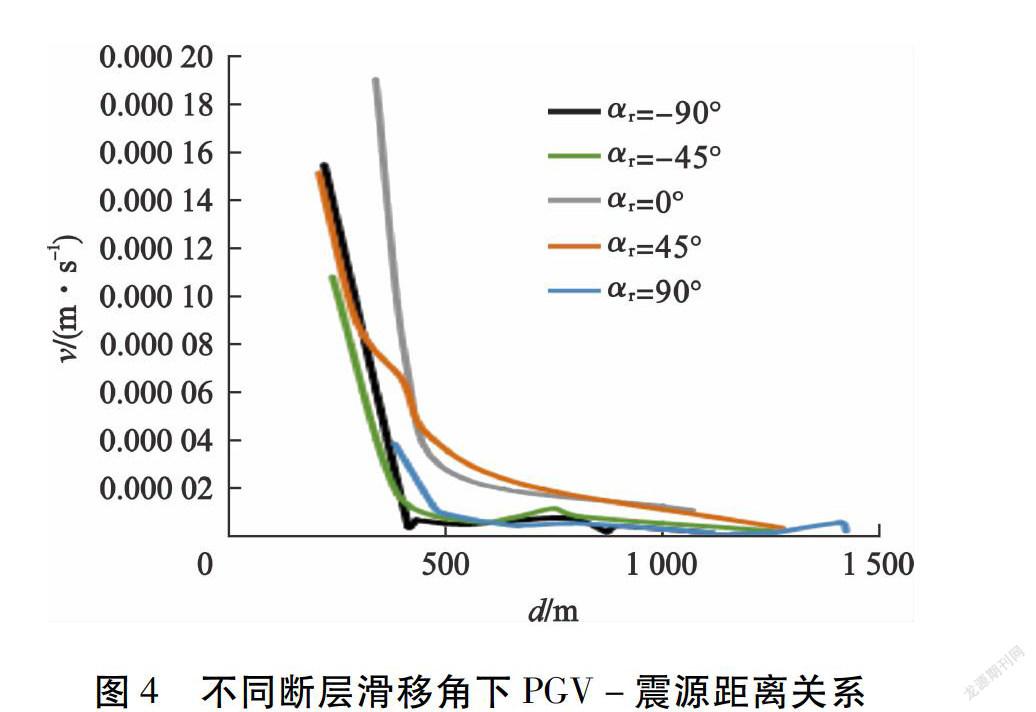
同断层滑移角对PGV分布的影响,在监测所得的数据中取滑移角(αr)为0°、45°、90°、-45°和-90°的5次震动事件,分别绘制PGV关于震源距离变化的曲线,见图4。
从图4可以看出:不同断层滑移角下随着震源距离的增大,所监测到的PGV值都在逐渐减小,整体上呈现出随震源距离增大而衰减的趋势,但在相同震源距离下,不同滑移角下的PGV值大小存在差异。
(1)整体上看,走滑断层(αr=0°)下的PGV值最大,且分布较为规律,其次是正断层(αr=45°)、垂直断层(αr=±90°),而逆断层(αr=-45°)下产生的PGV值最小。
(2)从曲线的走向和趋势上看,αr=-45°、αr=90°和αr=-90°的3条曲线较为吻合,呈现的规律性相似,特别是当d>600 m时,3条曲线几乎重合,说明逆断层和垂直断层PGV随震源距离分布具有一定的相似性,且这种相似性随与震源距离的增加而愈发明显。
2 PGV预测方法
对于爆破作业引起的震动事件,萨道夫斯基的经验公式[13],又称“Sadov公式”,是目前最为公认、应用面最广的经验公式,其具体表达式如下:
vs=K(Q1/3R)α(2)
式中:vs为测点最大震动速度(cm/s);K为与地形、爆破方式等因素相关的系数,坚硬岩石50~150,中等硬度岩石150~250,软岩250~350;Q为装药量(kg);R为测点距爆心的距离(m);α为爆破地震波衰减指数。
董陇军等[14]根据Sadov公式的原理,发现装药量对爆破威力的影响与地震动峰值速度反映出的爆破荷载的能量幅值具有相同趋势,基于上述理论,用震源PGV替代装药量Q作为计算参数,对Sadov公式进行了变形,从而得到新的围岩爆破震动峰值速度计算公式:
vb=m1v1/30/lm2(3)
式中:vb为质点震动峰值速度(m/s);v0为震源震动峰值速度(m/s);l为测点距爆心的距离(m);m1为受地形、爆破方式影响的相关系数;m2为震动波衰减系数。
对于非爆破事件引起的矿山震动事件,目前已有的PGV计算通用方程式大多是基于McGarr等人先前的工作:
lg Rvmax=AM+1(4)
式(4)变形可得:
vmax=C10AM/R(5)
式中:vmax为质点峰值速度(m/s);M为地震时间的震级;A和C為矿山特征参数。
1996年Kaiser对来自Brunswick矿山、El Teniente矿山和Creighton矿山的地震数据总体进行了95 %置信区间下的回归分析,综合McGarr 1984年的研究结果,确定参数A=0.5和C=0.25。因此,有:
vmax=C10a(Mw+1.5)R≈1.4×10(Mw+1.5)R(6)
式中:a为与矿山相关的特征参数。
由上述内容可知,目前国内外对PGV计算方法的研究已经较为成熟。但是,对经验公式在不同震动事件下适用性的讨论研究尚少,工程和研究人员在选择计算公式时缺少理论依据,所以需要结合现场数据对上述公式进行计算讨论,并将理论计算结果与实际监测值进行拟合,根据拟合的相关系数来确定不同公式的适用范围和精确度[15-16]。
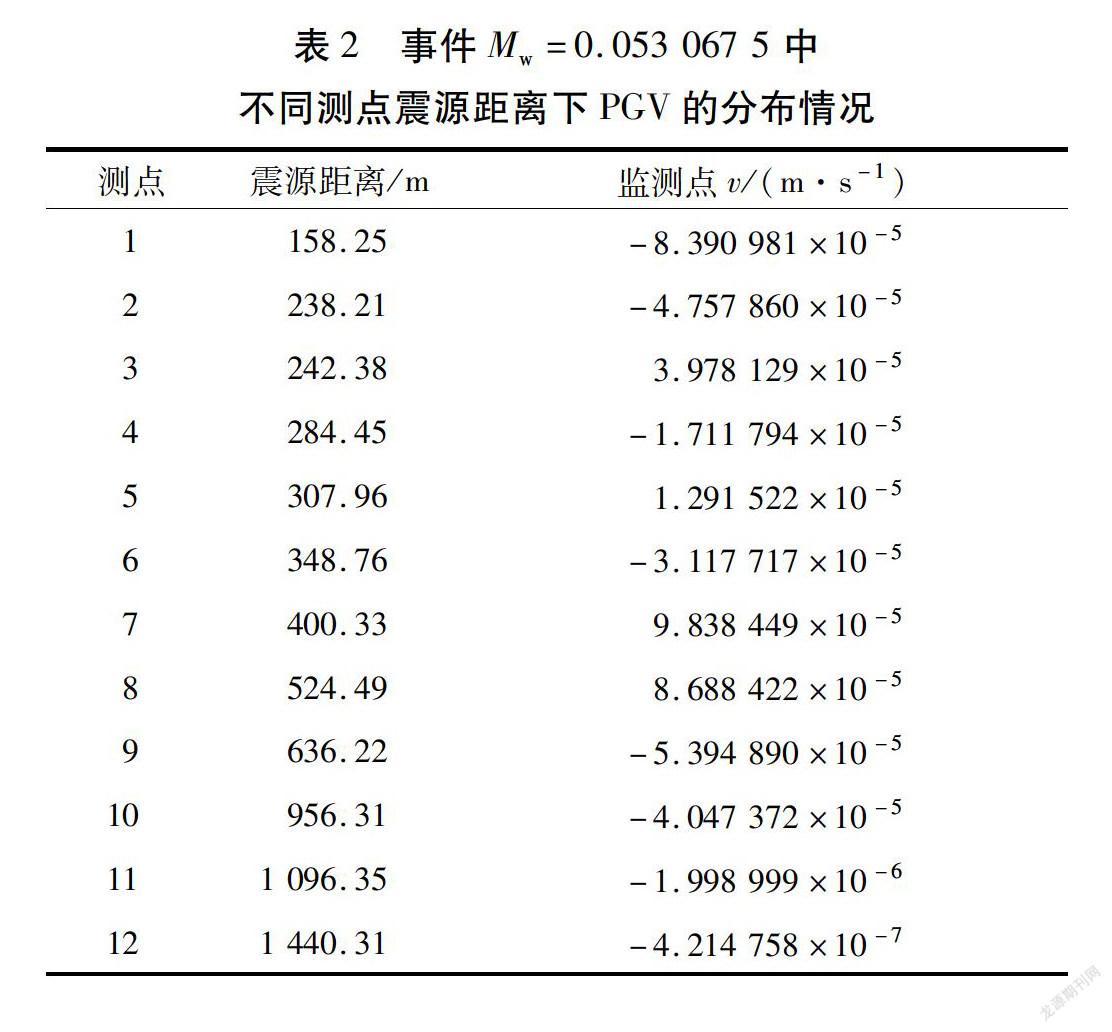
为了获得矿山特征参数,取Mw=0.053 067 5事件中的震源距离和实测PGV作为数据来源(见表2),对公式(5)进行迭代拟合运算,从而获得适用于金青顶矿区的特征参数:C=0.260 2和A=0.355 1。
此外,由于PGV和矩震级由震源能量释放决定,同时能量与速度的平方呈正相关,所以可将公式(3)
中的震源v0替换为矩震级Mw,得到公式(3)的变形公式:
vb=m1M1/6w/Rym2(7)
式中:Ry为测点距震源的距离(m)。
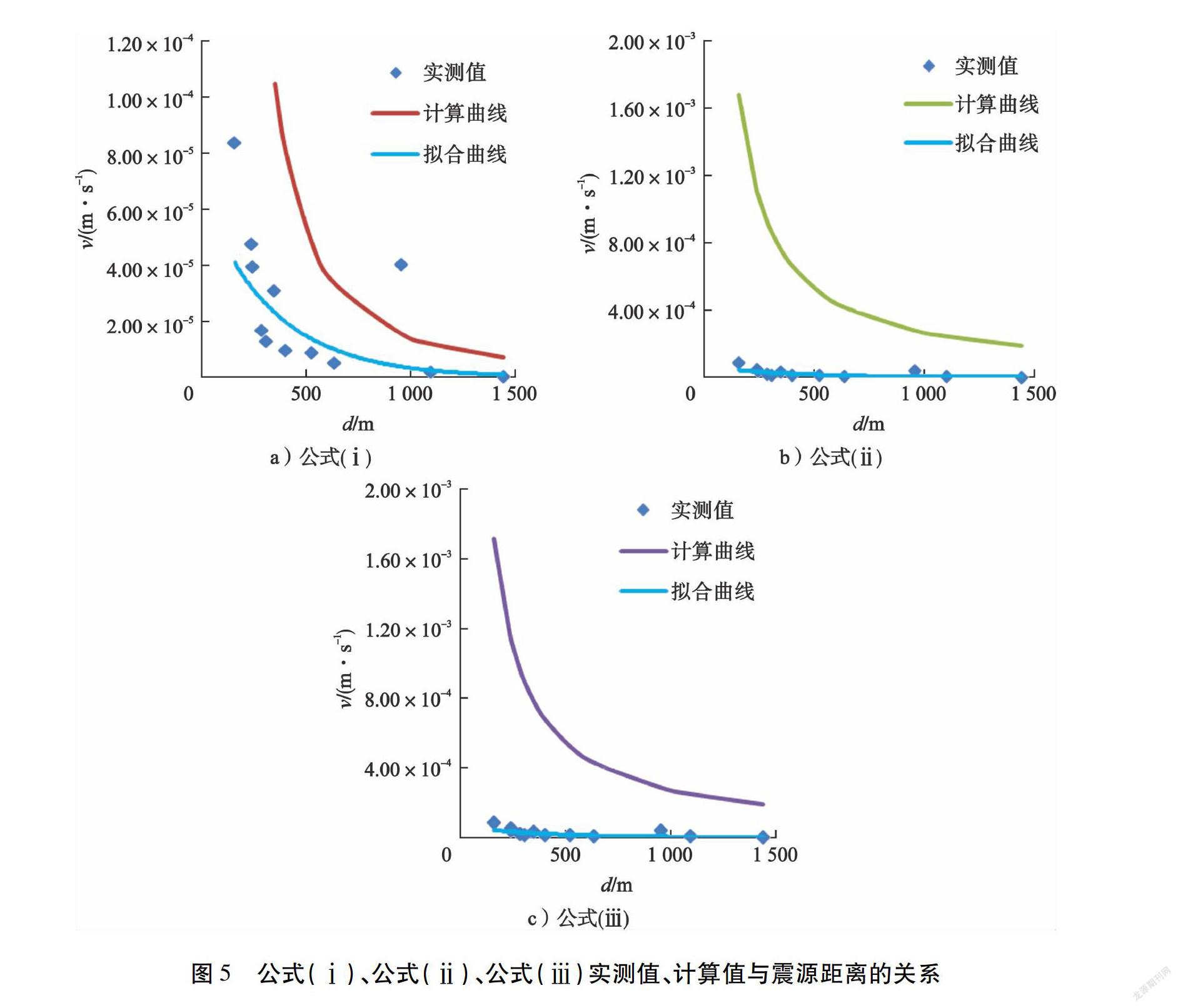
同样采用Mw=0.334 718 2事件中的数据对公式(7)进行迭代拟合,求得m1、m2的取值为18和1.9。 公式(7)、公式(5)和公式(6)的实际监测值、公式计算值与震源距离的关系曲线见图5(为表述方便,后文统称公式(ⅰ)、公式(ⅱ)、公式(ⅲ))。
对公式(ⅰ)、公式(ⅱ)、公式(ⅲ)的计算值与其对应的实测值进行相关系数拟合计算,获得3个公式的相关系数分别为r1=0.859、r2=0.798和r3=0.756。 结合实测值、计算值同震源距离的关系图及二者间的拟合相关系数,对3种PGV计算公式的拟合情况和适用性进行分析:
1)在3种公式的关系图中,PGV随震源距离的变化趋势皆与拟合曲线相同,说明3种公式中都体现了PGV随震源距离的衰减规律。
2)通过比较实测值的拟合曲线与3条计算曲线可发现,3条曲线在与拟合曲线的吻合度上存在差异,公式(ⅰ)计算曲线在d>500 m的区间内与拟合曲线有较高的拟合度,公式(ⅱ)和公式(ⅲ)整体上与拟合曲线有较大差异,说明3种PGV计算公式在当前情况下适用性不一。
3)比较三者的相关系数:r1=0.859>r2=0.798>r3=0.756,发现公式(ⅰ)的计算曲线和拟合曲线的吻合程度较高[17],证明公式(ⅰ)的函数曲线和PGV的实际分布规律高度相关,而公式(ⅱ)、公式(ⅲ)的拟合度较低,说明对于金青顶矿区的震动事件Mw=0.053 067 5而言,公式(ⅰ)的适用性优于另2种公式。
4)3种计算公式对该事件PGV计算所得结果仍存在较大误差。
针对3种公式在该事件中体现出的适用性差异,结合公式原理和震动事件本身的特征对误差进行分析:
(1)基于对原始数据的分析,了解到Mw=0.053 067 5 事件的震源以爆破作用为主导,而公式(ⅰ)是由Sadov 公式推导变形产生,Sadov公式是以爆破信号为震源的PGV计算公式,其计算原理和有关参数是基于爆破震动的形成机理和传播规律,所以理论上其变形公式更适用于围岩爆破震动峰值速度的计算[18];而公式(ⅱ)、公式(ⅲ)是基于McGarr经验公式的改进,其本身的参数A、C仅与矿山特征相关,而与爆破震动特征相关性较低,所以在计算非剪切作用为主导的震动事件时体现出较低的适用性。
(2)公式(ⅲ)中的矿山特征参数A、C源自于Kaiser对Brunswick矿山、El Teniente矿山和Creighton矿山的地震数据进行95 %置信区间下回归分析所得的结果,但理论上金属矿山间一般都存在较大的差异性,因此公式(ⅲ)中的特征参数缺乏普适性。
(3)因为深部金属矿在地质条件、采场结构和作业情况等方面都极为复杂,所以通过迭代拟合计算和总结出的爆破相关系数m1、衰减系数m2及矿山特征参数C、A可能与矿山实际情况不符,从而导致公式(ⅰ)及公式(ⅱ)的计算结果与实测值间存在一定差异。
3 基于监测数据与预测结果的支护建议
根据金青顶矿区的震动监测数据和分析结果,可以发现不同的震源参数会对采场及巷道围岩内的PGV分布产生明显的影响,且在同一震源条件下,PGV的分布在空间上表现出较强的不均匀性。因此,若在支护工作中不考虑震源参数对PGV分布规律的影响,则易导致出现支护手段与围岩稳定状态不匹配的现象[19-20]。根据Ju Ma等[12]提出的在考虑震源机制下的围岩支护设计建议,应基于该地区震动数据监测记录,对地震事件进行震源机制的反演分析,获得断层面解和矩震级的分布规律,根据所获取的断层面解和矩震级分布,合成该地区在可能的震源模型下及可能的最大矩震级风险下的PGV分布图,结合基于动态荷载和岩体质量等级的支护建议(见表3),采取适宜的支护手段。
由于公式(ⅰ)在该矿区条件下的适用性优于另外2种,所以选用Sadov公式的变形公式对矩震级Mw=1.65和Mw=0.99的2次震动事件中监测所得数据进行2种震源假设位置下的PGV分布预测分析。
3.1 震源位于采场M8-3~M8-5区域
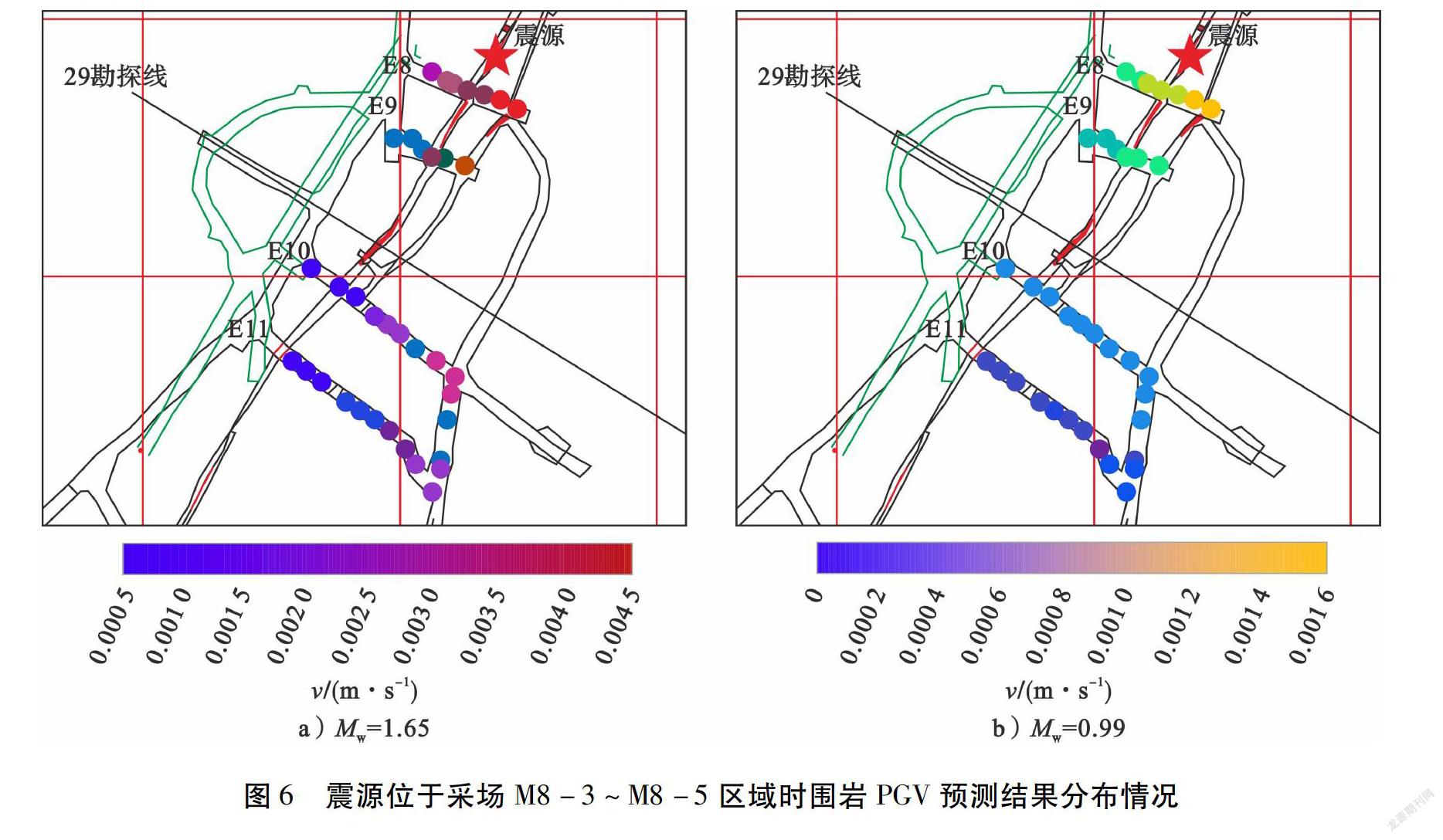
震源位于采场M8-3~M8-5区域内时所获得的E8、E9、E10和E11穿脉内围岩PGV预测结果分布情况见图6。
1)由图6-a)中的预测结果可知:在Mw=1.65震源条件下,E8、E9、E10和E11穿脉内围岩PGV預测最大值分别为0.004 46 m/s、0.004 22 m/s、0.002 89 m/s和0.002 47 m/s,根据表3对各穿脉内的支护作业给出如下建议:
(1)E8、E9穿脉内预测结果较大,建议对2条穿脉靠近采场位置的围岩进行喷射混凝土+普通锚杆支护,对存在节理裂隙的区域可利用锚网进行补充。
(2)E10、E11穿脉内围岩PGV预测值偏低,故整体上采用喷射混凝土作为支护手段。但是,E10、E11穿脉与采场的交叉区域内岩石暴露面积较大,应对该区域的围岩进行喷射混凝土+吸能螺栓+锚网的预支护。
2)由图6-b)中的预测结果可知:在Mw=0.99震源条件下,E8、E9、E10和E11穿脉内围岩PGV预测最大值分别为0.001 48 m/s、0.000 96 m/s、0.000 44 m/s 和0.000 19 m/s。通过与图6-a)所示结果比较可知:
(1)Mw=0.99震源条件下PGV随震源距离的变化趋势与Mw=1.65大致相同,但临近穿脉或采场间的PGV分布差异性较小,整体上PGV分布会更加均匀。
(2)根据上述现象,可将喷射混凝土作为各穿脉的通用支护手段,同时针对作业点附近的围岩或存在局部破碎的围岩,可考虑在喷射混凝土的基础上安装普通锚杆作为补充支护。
3.2 震源位于E10-1钻孔硐室内
震源位于E10-1钻孔硐室内时所获得的E8、E9、E10和E11穿脉内围岩PGV预测结果分布情况见图7。
1)由图7-a)中的预测结果可知:在该震源条件下,E8、E9、E10和E11穿脉内围岩PGV预测最大值分别为0.001 84 m/s、0.002 71 m/s、0.004 49 m/s和0.003 22 m/s,根据表3对各穿脉内的支护作业给出如下建议:
(1)E10穿脉内预测结果最大,且由于穿脉与采场及钻孔硐室相接,围岩的暴露面积大。故建议对E10穿脉靠近采场位置的围岩进行喷射混凝土+普通锚杆+锚网支护,对靠近主巷道的围岩进行喷射混凝土支护。
(2)E11穿脉内围岩PGV预测值偏低,建议对E11穿脉采用喷射混凝土的方式作为支护手段。由图7可知,E11、E10穿脉间采场内的预测值偏大,且该采场内顶板围岩破碎并已设置木桩支护,所以建议在木桩支护的基础上添加喷射混凝土+普通锚杆作为补充支护。
(3)E8、E9穿脉内PGV预测值普遍低于0.002 5 m/s,故对E8、E9穿脉围岩采取喷射混凝土支护即可。
2)由图7-b)中的预测结果可知:在Mw=0.99震源条件下,E8、E9、E10和E11穿脉内围岩PGV预测最大值分别为0.000 12 m/s、0.000 67 m/s、0.001 50 m/s 和0.001 48 m/s,根据表3对各穿脉内的支护作业给出如下建议:
(1)图7-b)中各穿脉内PGV值都较小,说明该情况下震动对围岩稳定性的影响较弱,且各穿脉间PGV分布的差异性较低,所以建议对E8、E9、E10和E11穿脉内的围岩采用喷射混凝土支护。
(2)由于E10穿脉与采场及钻孔硐室相接,其围岩的暴露面积大。故建议对E10穿脉靠近采场位置的围岩进行喷射混凝土+普通锚杆支护。
4 结 论
本文在研究国内外震动机理和相关理论的基础上,采用理论分析、现场监测数据分析和拟合相关系数计算等手段对不同震源参数下PGV分布规律和预测技术进行了深入研究和分析,得出以下结论:
1)震源距离对PGV分布产生明显作用;且PGV随震源距离的衰减程度与震源距离之间存在密切的联系,当距震源较远时,震源距离对PGV的衰减作用逐渐弱化。
2)相同震源距离下的PGV会随矩震级增大显著变大,且这种影响会根据距震源远近逐渐衰减。
3)不同的断层滑移角下的PGV大小和分布情况存在较大差异,一般情况下走滑断层(αr=0°)>正断层(αr=45°)>垂直断层(αr=±90°)≈逆断层(αr=-45°)。
4)Sadov公式的变形公式在爆破条件下PGV计算中体现出良好的适用性,同时也说明运用与震动事件的类型和机理相符的公式,所得结果更能反映PGV的实际分布规律。
5)通过迭代拟合获得的McGarr经验公式中的特征值A、C不能完全适合该矿区,且Kaiser回归分析获得的特征值在特定矿山下缺乏适用性,导致计算结果与实测值间的相关性较低。
6)在制定采场或巷道的支护方式时,应结合不同震动事件下,支护区域及周边围岩的PGV分布情况,根据不同震源机制下的围岩支护设计建议选择更加合理和时效化的支护方式。
[参 考 文 献]
[1] MORRISION R G K.Theory and the practical problem of rock bursts[J].Engineering and Mining Journal,1948,149(3):66-72.
[2] 冯叔瑜,吕毅,顾毅成.城市控制爆破[M].北京:中国铁道出版社,1987.
[3] 何姣云.矿山采动灾害监测及控制技术研究[D].武汉:武汉理工大学,2007.
[4] 熊仁钦.顶板大面积来压破坏机理的研究[J].煤炭学报,1995(增刊1):38-41.
[5] 陈寿如,宋光明,史秀志,等.近河堤采矿爆破的震动监测与控制[J].中国有色金属学报,2000,10(1):136-139.
[6] 韩子荣.金川矿区露天地下联合开采的爆破震动安全性评价[J].矿冶工程,1985,5(1):6-11.
[7] 王民寿,郭庆海.用双随机变量回归改进爆破震速回归分析[J].爆炸与冲击,1998,18(3):283-288.
[8] 徐全军,刘强,聂渝军,等.爆破地震峰值预报神经网络研究[J].爆炸与冲击,1999,19(2):133-138.
[9] 徐全军,张庆明,挥寿榕.爆破地震峰值的神经网络预报模型[J].北京理工大学学报,1998,18(14):472-475.
[10] 黄光球,桂中岳.确定爆破工程中真实经验公式的遗传规划方法[J].工程爆破,1997,3(3):15-22.
[11] 熊代余,顾毅成.岩石爆破理论与技术新进展[M].北京:冶金工业出版社,2002.
[12] MA J,DONG L J,ZHAO G Y,et al.Qualitative method and case study for ground vibration of tunnels induced by faultslip in underground mine[J].Rock Mechanics and Rock Engineering,2018,52(3):1-15.
[13] 田蜜.爆破扰动诱发煤矿冲击地压的数值模拟研究[D].阜新:辽宁工程技术大学,2014.
[14] 董陇军,王钧晖,马举.不同微震震源机制下地下硐室围岩响应及支护建议[J].隧道与地下工程灾害防治,2019,1(3):68-76.
[15] 肖和平.煤矿构造矿震机理[J].湖南地质,1999,18(2/3):141-146.
[16] 肖和平.煤矿矿震应力窗口效应[J].华南地震,1999,19(1):85-90.
[17] 董陇军,李夕兵,唐礼忠,等.无需预先测速的微震震源定位的数学形式及震源参数确定[J].岩石力学与工程学报,2011,30(10):2 057-2 067.
[18] 邹景波.爆破地震波作用下结构的动力响应及安全评价研究[D].青岛:青岛理工大学,2012.
[19] 毛晖.建筑物爆破震動的安全控制技术研究[D].长沙:中南大学,2004.
[20] 许红涛,卢文波.几种爆破震动安全判据[J].爆破,2002,19(1):8-10.
Study on the distribution and prediction of PGV in surrounding
rock under different seismic source parameters
Wang Xi1,Li Shiqing2,Li Qiutao2,Cheng Li1,Liu Huanxin1
(1.Deep Mining Laboratory Subsidiary of Shandong Gold Mining Technology Co.,Ltd.;
2.Shandong Jinzhou Mining Group Co.,Ltd.)
Abstract:In order to totally understand the law of seismic wave propagation and distribution in the surrounding rock under different seismic source mechanisms,the paper studies the distribution of PGV under different seismic source parameters based on field monitoring data.The results show that the distance between stations and the source,moment magnitude scale,and the rake of fault slip have different effects on the distribution of PGV.The applicability of each prediction methods is analyzed by comparing the fitting correlation coefficient between PGV calculated from empirical formulas and others from field monitoring.The study finds that the predicted value of PGV calculated from the Sadovs prediction formula has a higher correlation to the measured result with blasting vibration event.Based on the above research results,the spatial distribution of PGV under dynamic seismic mechanisms is calculated before suggestions on the surrounding rock support under different conditions of the seismic source location and magnitude are given.
Keywords:metal mine;seismic source;vibration monitoring;PGV;prediction formula;fitting correlation coefficient
