正态分布及其实际应用

随着计算机的广泛使用和人工智能时代的来临，数据量越来越庞大，如何处理这些数据？如何从数据中发现规律，提炼出有价值的信息？这些都是非常重要的问题，为此，很多人开始从事这些问题的研究工作，他们被称为数据挖掘工程师，现在，让我们一起来探索数据挖掘中的奥妙，

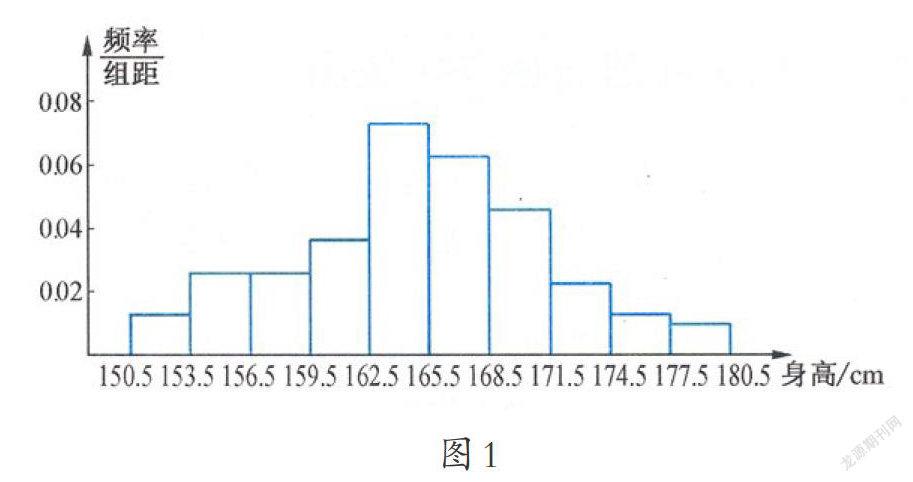
举一个身边的例子，我们先观察某中学男生的身高数据，从中找出身材最高和最矮的同学，或者算出他们身高的平均值，如果我们想要知道男生身高数据的分布情况，比如1.7米至1.75米之间有多少人，占所有男生的比例是多少，我们应该怎么做？如图1所示，我们可以画出频率分布直方图，将身高最小值至最大值这一区间等分成若干组，统计每一组男生的人数和频率，然后，在平面直角坐标系中，用横坐标代表身高，纵坐标是每个小组的频率除以相应的组距，并绘制出相应的矩形，每个矩形的面积就是该小组男生身高的频率。

从身高的频率分布直方图中我们可以看到，数据大致呈现“中间高，两边低”的特点，在十六七岁的男生中，身高超过1.85米和低于1.5米的人数都非常少，而大部分人的身高集中在1.6米至1.75米之间，因此，虽然每个人的身高具有随机性，但对同一年龄、同一性别的人群来说，其身高的分布是有规律的。

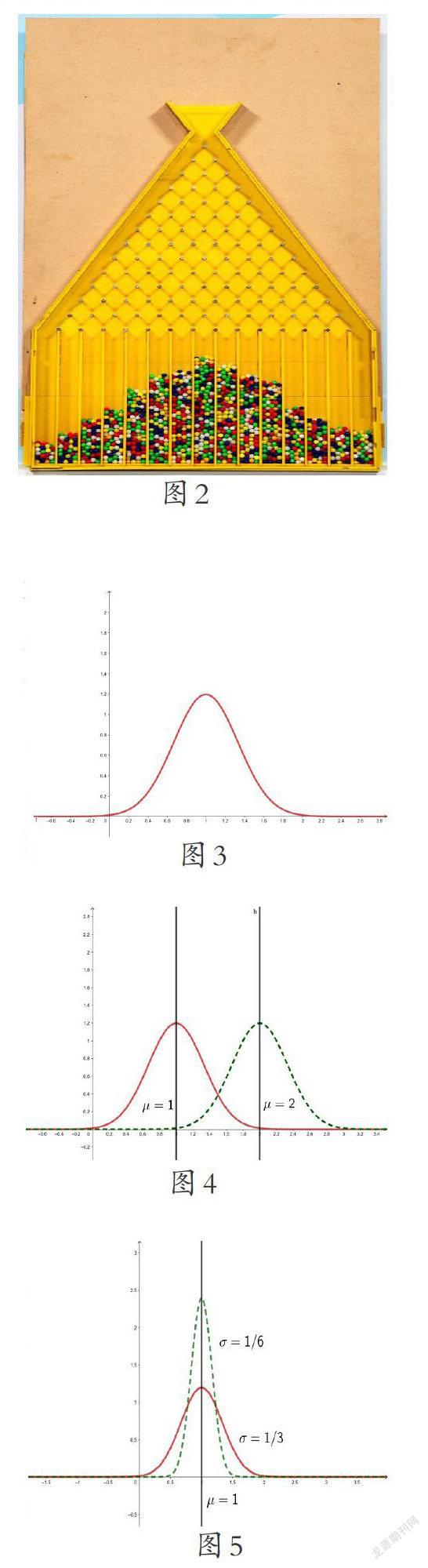
这种规律性是只在身高数据中体现，还是在自然界中普遍存在呢？英国生物统计学家法兰西斯·高尔顿做了一个实验，他在一块木板上画了一块等腰三角形，并在三角形区域内钉上n+1层钉子，第1层钉2个钉子，第2层钉3个钉子，下面每一层都比上一层增加1个钉子，上一层的每个钉子都在下一层2个钉子的中间位置，之后，在第n+1层的下面，放人n+2个球槽。

建成后，高尔顿从顶端逐个扔下小球，这些小球在下落的过程中与众多钉子发生碰撞，每次碰撞都会使得小球随机向左或向右下落，随着小球个数的增加，掉入各个球槽内的小球的个数会越来越多，堆积的高度也会不断增加，最终，如图2所示，各球槽将呈现出“中间高，两边低”的分布，这与我们身高数据的分布非常相似。

并且，如果进一步增加钉子的层数和小球的个数，球槽中小球分布形成的曲线就会越来越光滑，最终趋向于图3“中间高，两边低”的“钟型”曲线，我们将这条曲线称为正态分布密度曲线，简称正态曲线。

我们通过观察这条曲线可以发现，正态曲线是单峰的，有一条对称轴，对称轴所在的位置正是数据的平均值，用字母u表示，例如我们的平均身高等。对比图4中的两条正态曲线，我们可以看出虚线对应的平均值更大，

图5中两条正态曲线的平均值相同，但是形状不同，实线的正态曲线更加“矮胖”，而虚线的正态曲线更加“高瘦”，我们用另一个希腊字母σ（σ>0）来反映这种“矮胖”或“高瘦”的程度，假设这两条曲线分别代表了两个班学生成绩的分布情况，两个班学生的平均成绩相差较小，但虚线对应的班级，学生的成绩更集中于平均成绩附近，它的σ小，而实线对应的班级，學生的成绩相对分散，它的σ大，可能出现两极分化的情况，所以，σ反映了数据的离散程度，它代表了数据的标准差，知道了u和σ这两个参数，我们就能画出正态曲线。

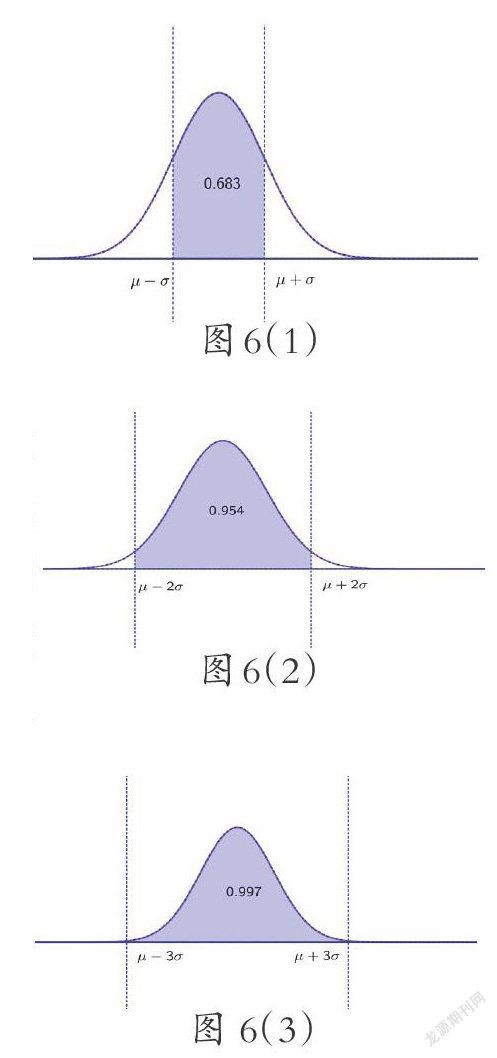
我们也可以从另一个角度理解σ，正态曲线与直线x=a，x=b和x轴所围成图象的面积代表了数据在区间（a，b）所占的比例，假设工厂生产某种零件，要求孔径为10mm，但在实际生产中会有误差，如果孔径的分布近似服从平均值为10mm、标准差为0.1mm的正态分布，那么如图6（1）（2）（3）所示，孔径落在9.9-10.1这一范围的比例应该是0.683.这是数据分布的主体孔径落在9.3-10.3这一范围的比例应该是0.997.落在该区间之外的机率非常小，如果出现比较多的产品超出了这一范围，那么我们可以怀疑生产过程出现了问题，这称为“3σ原则”，在生产的过程中，我们可以根据这一原则进行产品质量检测。

正态分布在统计中是很常用的，例如在医学上，可以运用正态分布估计人体的某些生理指标，比如白细胞数的正常值范围，白细胞数在正常人群中近似正态分布，我们可以制定一个上限和下限，比如95%的人在正常范围之内，而超出这一范围的人，我们就认为需要对其进行特殊关注了。