露天矿山台阶爆破矿岩平均块度的FOA-SVM预测

摘要：露天矿山台阶爆破后矿岩的平均块度是衡量爆破质量的重要指标，对后续的铲装和运输也具有重要的意义。为了对台阶爆破后的矿岩平均块度进行预测，使用果蝇优化算法（FOA）对支持向量机回归模型（SVM）进行参数优化，通过建立基于果蝇优化算法的支持向量机回归模型（FOA-SVM）对矿岩爆破平均块度进行预测，避免传统的SVM参数选取对预测结果准确性产生的影响。结果表明，FOA-SVM可实现对矿岩爆破平均块度的较好预测。

关键词：露天开采;台阶爆破;平均块度;果蝇优化算法;支持向量机;预测

中图分类号：TD235

文章编号：1001-1277（2020）02-0043-04

文献标志码：Adoi：10.11792/hj20200208

引 言

露天开采过程中，矿岩的爆破块度一直是衡量矿山爆破质量好坏的重要指标之一，合适的爆破块度对于矿岩的铲装及运输效率起着十分重要的作用。块度太大，挖掘机在铲装过程中需要不断地将其挑出，进行二次解小，不但影响铲装效率，同时还影响平台的推进;块度过小，说明炸药单耗过高，在爆破过程中容易产生爆破飞石，不利于安全生产，且矿石过于破碎，铲装运输过程中容易导致粉矿丢失，使得采矿损失率增大，造成经济损失。因此，合适的爆破块度便成为露天矿山台阶爆破所要求达到的目标。

研究表明，矿岩的爆破块度与爆破设计参数、炸药性能及矿岩性质等诸多因素有关[1]，各因素彼此之间又是极为复杂的非线性关系。为了对矿岩爆破块度进行预测，研究人员将人工智能理论引入矿岩爆破块度预测中，如人工神经网络[2]、BP神经网络[3-4]、支持向量机[5-6]、最小二乘法[7]等，但预测准确度还有待提高。

支持向量机（Support Vector Machine，SVM）[8]综合分析了影响矿岩爆破块度的诸多要素，不但在非线性映射能力及泛化能力上具备优势，而且在预测精度、收敛速度、模型稳定性及可重复训练方面也得到加强，但其缺点在于预测的准确性与惩罚参数（C）和核参数（g）的选取密切相关。而只有2个调节参数的果蝇优化算法（Fruit Fly Optimization Algorithm，FOA）[9]极大地减少了计算量，有较强的全局搜索能力，可以实现SVM的惩罚参数和核参数的动态调整。因此，本文正是借助FOA的优点来构造基于果蝇优化算法的支持向量机回归模型（FOA-SVM），并采用MATLAB软件来仿真预测台阶爆破矿岩块度，以期实现对矿岩爆破块度的较好预测。

1 支持向量机

SVM基本理论是借助非线性映射算法将原始数据从低维空间线性不可分的样本转化到高维特征空间，并解决此特征空间中的线性回归问题[10]。

若假设样本V=（xi，yi）pi∈Rp × R，其中，xi∈Rp为输入参数，而yi∈R则是与之对应的输出参数，p为样本个数。那么SVM的回归函数可以表示为：

f（x）=b+ω·φ（x）（1）

式中：b为阈值;ω为权值矢量;φ（x）为高维核心诱导特征空间。

依据统计理论，可通过以下目标数极小化确定SVM 回归函数：

f（x）=min1[]2‖ω‖2+C∑pi=1（ξi+ξ*i）（2）

式（2）的约束条件如下：

s.t.yi-f（xi）≤ε+ξi

f（xi）-yi≤ε+ξ*i

ξi，ξ*i≥0

式中：ξi、ξ*i为非负松弛变量;C为惩罚参数;ε为不敏感损失函数参数。

借助拉格朗日方法对式（2）的约束最优化问题进行求解，从而把原问题改为双拉格朗日形式，即：

J（ai，a*i）=max1[]2∑pi=1∑pj=1（ai-a*i）（aj-a*j）+

K（xi，xj）+∑ni=1ai（yi-ε）（3）

式（3）的约束条件为：

s.t.∑pi=1（ai-a*i）

ai，a*i∈[0，C]

式中：J（ai，a*i）為拉格朗日函数;K（xi，xj）为径向基核函数，K（xi，yi）=exp（-g|xi-xj|2），g为核函数;ai，a*i为拉格朗日系数。

综上，SVM的回归函数可表达为：

f（x）=b+∑pi=1（ai-a*i）K（xi，xj）（4）

在SVM模型中，惩罚参数、核函数及不敏感损失函数参数都是用户定义的参数，在迭代过程根据完整训练数据集选择最佳值。因此，参数的选取合理与否，对于SVM预测结果的准确性有着重要影响。

2 果蝇优化算法

果蝇优化算法是专家学者在果蝇寻找食物的过程中推演得到的一种寻求全局最优的方法，已经在不同领域得到了普遍的应用，和其他群体智能算法不同之处在于，果蝇优化算法仅有2个调节参数（进化代数和种群规模），从而大大减小了计算量，全局搜索能力也得到加强。果蝇是循着食物的气味从远处一直搜索到食物附近，然后通过视觉发现食物的位置。当一群果蝇在群体初始位置向各个方向随机搜寻食物时，一旦其中某只果蝇嗅到的食物气味浓度最浓，并向周围果蝇发送气味信息，其他的果蝇便会飞往它的位置（见图1）。在新的位置果蝇们再次沿随机方向飞出，如此反复，直到果蝇发现食物的所在。

果蝇优化算法从果蝇的过程行为，归纳出下述几个步骤[11]：

1）首先对果蝇群体的初始位置进行初始化，设定该果蝇的种群规模n及所需的最大迭代次数。

2）对群体中个体利用其嗅觉搜寻食物的随机方向和距离进行赋值。

3）计算果蝇i与原点之间的距离D（p，i），然后计算味道浓度判定值S（p，i）=1[]D（p，i）。

4）根据计算得到的S（p，i）计算单只果蝇位置的味道浓度Smelli=f（S（p，i））。

5）保留上一步骤中的最佳味道浓度max（Smelli）及其坐标位置。

6）果蝇迭代寻优开始，重复步骤2）～4），如果Smelli大于前一迭代的味道浓度值，则执行步骤5）。

3 FOA-SVM

利用果蝇优化算法对SVM的惩罚参数和核参数进行动态调整，提升模型的侦测能力，进而使预测的精确度得以提高。其基本流程为：

1）随机化果蝇群体的初始位置范围，确定果蝇的种群规模n及最大的迭代次数maxgen。

2）果蝇寻优开始，对果蝇个体寻找食物的随机飞行方向与距离区间进行设定，初始化单只果蝇的飞行距离x（i，：）、y（i，：）、z（i，：）。

x（i，：）=x1+Rran

y（i，：）=y1+Rran

z（i，：）=z1+Rran（5）

式中：Rran为随机数;x1、y1、z1为果蝇初始空间方位。

3）计算单只果蝇i与原点之间的距离D（i，：）。

D（i，：）=[x（i，：）]2+[y（i，：）]2+[z（i，：）]2（6）

4）计算味道浓度判定值S（i，：），并通过S（i，：）对C和g进行赋值。

S（i，：）=1[]D（i，：）（7）

C=20S（i，1）（8）

g=S（i，2）（9）

5）果蝇迭代寻优开始，设定gen=1：maxgen，重复步骤2）～4），如果味道浓度大于前一次迭代的值，则保留当前最佳味道浓度及与之对应的坐标值，算法终止后得到最优的FOA-SVM，最后利用训练好的模型来预测矿岩爆破平均块度。

4 实例分析

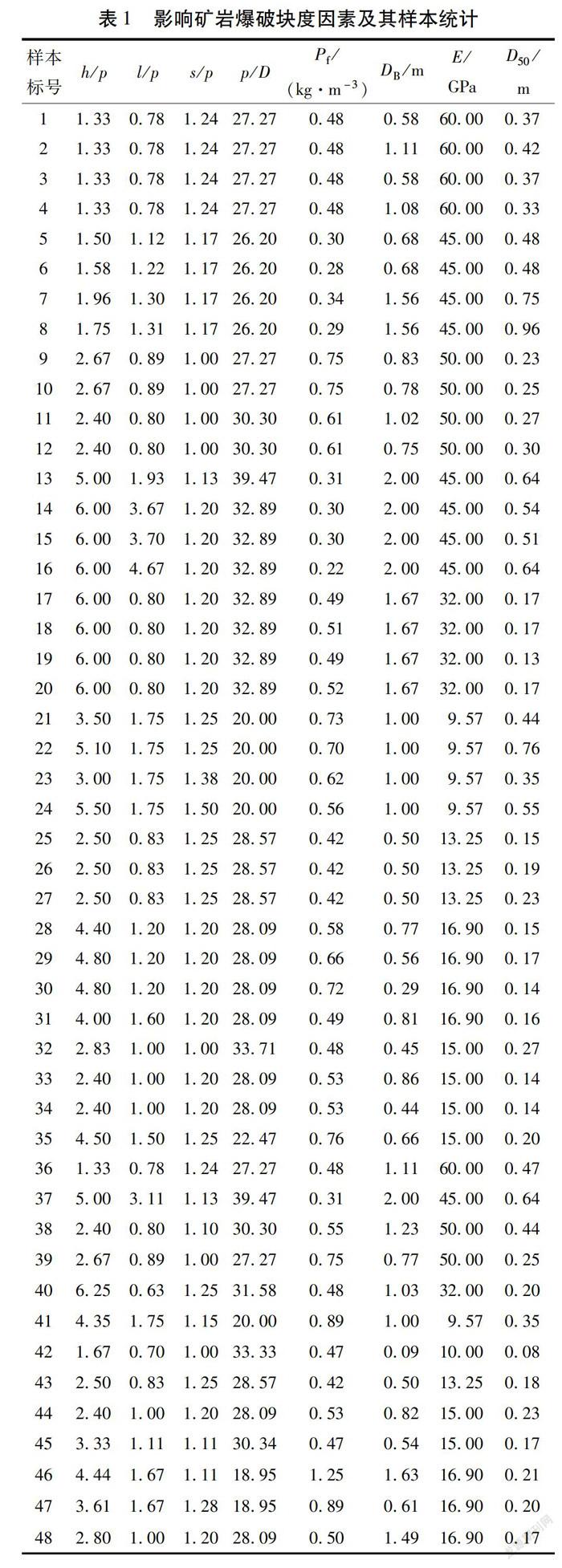
本文选用文献[8]中的矿岩爆破块度进行研究，选取台阶高度与炮孔荷载比（h/p）、炮孔充填长度与荷载比（l/p）、排间距与荷载比（s/p）、荷载与孔径比（p/D）、粉末因子（Pf）、弹性模量（E）和爆破矿岩块度（DB）等7个参数作为矿岩爆破块度的预测依据，爆破矿岩的平均块度（D50）作为输出参数，各参数具体数值见表1。

将表1中的1～35组数据作为训练样本，36～48组数据作为预测样本，同时选取台阶高度与炮孔荷载比（h/p）、炮孔充填长度与荷载比（l/p）、排间距与荷载比（s/p）、荷载与孔径比（p/D）、粉末因子（Pf）、弹性模量（E）和爆破矿岩块度（DB）的归一化数据为7个输入数据。预测样本的预测结果见图2、图3，并将预测结果与其他几种算法进行对比，对比情况见表2。

与实际情况进行比较发现，FOA-SVM仅在预测44号样本时出现较大偏差，其余预测结果均与实际值相符，其平均误差仅为2.05  %;相对单纯使用SVM预测，平均误差降低了2.94百分点，而BP神经网络及最小二乘法预测的平均误差分别为15.71  %、27.32  %，遠远高于FOA-SVM。

5 结 论

1）采用FOA对SVM的惩罚参数和核参数进行动态调整，可以避免传统SVM参数选取对预测结果的准确性产生影响，不仅保留了SVM的优点，还提高了模型的侦测能力。

2）在使用FOA-SVM对矿岩爆破平均块度进行预测，并将预测结果与其他多种算法的预测结果进行比较的过程中可以看出，FOA-SVM能够更为精准地预测不同爆破参数条件下矿岩爆破平均块度，而且可以根据现有的实测数据，通过调整台阶爆破参数实现矿岩爆破平均块度的快速预测，从中选择符合矿山生产的台阶爆破参数。

[参考文献]

[1] KULATILAKE P H S W，WU Q，HUDAVERDI T，et al.Mean particle size prediction in rock blast fragmentation using neural networks[J].Engineering Geology，2010，114（3/4）：298-311.

[2] MONJEZI M，AMIRIH，FARROKHI A，et al.Prediction of rock fragmentation due to blasting in Sarcheshmeh copper mine using artificial neural networks[J].Geotechnical and Geological Engineering，2010（28）：423-430.

[3] 李义炜，张永贵，赵井清，等.基于BP神经网络的中深孔爆破块度预测[J].化工矿物与加工，2012，41（2）：28-30.

[4] 史秀志，郭霆，尚雪义，等.基于PCA-BP神经网络的岩石爆破平均粒径预测[J].爆破，2016，33（2）：55-61.

[5] 魏春启，李昂，曹兰柱.基于支持向量机模型爆破块度预测[J].应用泛函分析学报，2015，17（4）：415-422.

[6] 潘玉忠，张义平，王强，等.台阶爆破块度的SVM预测模型研究[J].矿业研究与开发，2010，30（5）：97-99.

[7] 史秀志，王洋，黄丹，等.基于LS-SVR岩石爆破块度预测[J].爆破，2016，33（3）：36-40.

[8] SHI X Z，ZHOU J，WU B B，et al.Support vector machines approach to mean particle size of rock fragmentation due to bench blasting prediction[J].Transactions of Nonferrous Metals Society of China，2012，22（2）：432-441.

[9] PAN W T.A new fruit fly optimization algorithm：Taking the financial distress model as an example[J].Knowledge-based Systems，2012，26：69-74.

[10] 张宏伟，朱志洁，霍丙杰，等.基于改进的FOA-SVM导水裂隙带高度预测研究[J].中国安全科学学报，2013，23（10）：9-14.

[11] 赵国彦，林春平，洪昌寿.基于FOA-GNNM的矿井突水水源判别[J].世界科技研究与发展，2015（6）：673-675.

Prediction of average block size of rock in open-pit

mine bench blasting based on FOA-SVM

Lin Chunping

（Zijin Mining Group Co.，Ltd.）

Abstract：The average block size of rock after bench blasting in open-pit mine is an important measurement for blasting quality.It is also significant for subsequent shoveling and transportation.In order to predict the average block size after bench blasting，the parameters of Support Vector Machine（SVM）were optimized using Fruit Fly Optimization Algorithm（FOA）.By establishing FOA-SVM，the average block size of rock after blasting is predicted.The impact of traditional SVM’s parameters selection on the accuracy of the prediction results is avoided.The results show that the FOA-SVM can achieve a better prediction of the average block size of rock blasting.

Keywords：open-pit mine;bench blasting;average block size;Fruit Fly Optimization Algorithm;support vector machines;prediction

收稿日期：2019-08-04; 修回日期：2019-09-20

作者簡介：林春平（1990—），男，福建龙岩人，工程师，硕士，从事露天矿山采矿技术研究工作;福建省龙岩市上杭县紫金大道1号，紫金矿业集团股份有限公司，364200;E-mail：710114643@qq.com