让“数概念”教学直观、丰满起来

邱杭

摘要：数概念对学生而言，常常很抽象、枯燥，这给学生理解和教师的教学带来诸多挑战，教学中怎样有效落实？有没有办法让数概念更形象化，直观化，具体化？让零散的、复杂的概念立体丰满起来？笔者借助曾上过的《真分数和假分数》一课作为载体，尝试解决以上问题。

关键词：具体情境 数轴 沟通联系。

中图分类号：G4 文献标识码：A 文章编号：（2020）-23-

自然数、整数、小数、分数、百分数等，都是小学数学中最基本的概念，这些概念都是学生今后构建“概念网络图”、学习数的运算、研究数量关系的重要基础，是小学数学中的核心内容。

那么如何让枯燥、抽象的数概念立体、丰满起来，笔者借着自己曾上过的《真分数和假分数》为例，谈一谈让数概念教学的有效途径和方法。

一、让学生在具体情境中认数。

教学实践证明，理解数的意义，既需要从数的组成去建构，又需要联系实际来体会。因此教师在课堂教学中，要注意创设生活情境运用具体事例，去激发学生的求知欲，为学生创设乐学的前提条件，同时消除学生对数学概念学习的枯燥感，把数学概念教学植根于一个现实需要的问题情境之中，让数学问题变得十分鲜活。笔者在教学“真分数和假分数”时是这样设计的：

出示□/4，复习分数的意义。

师：如果这是一个分数，方框里能填什么数？

生：1/4……

师：板书：1/42/4  3/4  4/4  5/4  ……

师：这么多的分数，要想把他们分别在圆片上用阴影表示出来，你会表示哪个分数？

生举例，师贴出相应的阴影圆片

师：指着4/4，在这张圆片中一个有几个1/4？

在学生确认4个1/4后，教师指出：把单位“1”平均分成4份，其中任何一份都是它的1/4.1/4也就是分数单位。

师：在1/4的基础上增加一个1/4是（2/4）

师：在2/4的基础上增加一个1/4是（3/4）

师：在3/4的基础上增加一个1/4是（4/4），也就是1。

师：继续推算，4/4再加一个1/4是多少呢？你能在圆片上把它表示出来吗？

……

这样的引入设计，是基于以下思考：自然数是“十进位值制”的，不同计数单位与其个数的累加就构成了全部的自然数。

二、让学生借助学习工具——数轴来认识数

数是比较抽象的数学概念，挖掘和利用概念中的直观成分，能有效地降低教学的难度。而数轴则是实现了数与形的第一次联姻，使数与直线上的点建立了对应关系，揭示了数与形的内在联系，并由此成为数形结合的基础，使抽象的数成为有形可依。因此数轴是学习有理数及以后学习无理数的工具。

基于这样的思考笔者在设计《真分数和假分数》一课时是这样设计的：

1、出示数轴

出示：

师：1/3，3/6如果要把他表示在数轴上，会在哪个范围内？

生：0～1之间

师：包括1吗？他也不包括0，所以老师在0和1上用“。”表示出来，就是不包括0和1.

出示：

在数轴上表示出：1/3，和3/6

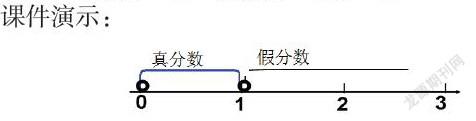
2、观察，这些真分数与假分数在数轴上的位置，你有什么新的发现？

生：……

师：真分数在0～1之间，就表示真分数比1要小，而假分数在1和1的后面就表示假分数=1，或大于1.

板书：真分数<1    假分数>1或=1

课件演示：

三、沟通联系，促进意义建构

受小学生思维发展水平和接受能力的限制，有些知识的教学往往是分几课时或几个学期来完成，这样难免在不同程度上削弱知识间的衔接，因此要以旧知为着眼点，提供探究的时空，发挥学生的创造性思维，激发学生自己主动探究，经过多层次的反复的比较，概括，分析与综合，建构数学概念。如在《真分数和假分数》教学中就有以下的设计 ：

1、用数字组成分数，并用图形表示

师：给你8和5能组成真分数和假分数吗？

生：真分数5/8，假分数8/5

师：你能自己画图表示5/8和8/5的意义吗？

学生用圆形、长方形、正方形、直线等图表示出5/8和8/5。

组织学生再次思考：8/5为什么要用到两幅图来表示，学生根据作品解释意义。

2、结合具体问题选择分数5/8和8/5。

1）一条路已经修了（   ）    2）一根绳子长（   ）米。

思考：可以填哪些分数？为什么？

追问：如果把1米看做单位“1”那5/8米比1米长还是短？8/5米呢？

数概念是人类经过成千上万年才获得的抽象概念，数概念的学习相对而言又是儿童数学能力发展中的一个难点。只有架起了“数”与“形”之间的桥梁，才能让数概念教学直观起来，以“点”带“面”注重前后联系，才能让数概念教学立体、丰满起来。

参考书目

[1]宋煜阳.联系沟通 理解意义——“真分数和假分数”教学实录与评析[J].上海教育出版社.小学数学教师.2013，1，2.

[2]张丹著.小学数学教学策略 [M].北京大學出版社，2010年.