车内低频结构耦合噪声板件贡献量分析

吴明钦 周龙龙

摘要：通过对车身板件声学贡献分析得出车室特性声学特性，推导封闭空间板件振动在空间内产生的辐射噪声，结合车室壁板计算车身板件声学贡献量，在考虑到目标点位置权重与相对噪声水平系数提出板件综合声学贡献量系数。为了确定车身需要优化的板件，通过声-固耦合有限元模型利用边界元法确定车内目标点的频响曲线，计算出声腔结构划分出的车身峰值频段下的车身板件综合声学贡献量系数。在Isight中用最优拉丁超立方法对需要优化的7块板件于设计空间内抽取50组样本，在有限元模型中计算目标响应，根据7块板件厚度参数因子与4个目标响应，运用径向基神经网络模型（RBF），建立精度较高的车身板件近似模型。

关键词：板件声学贡献量;频响曲线;近似模型;拉丁超立方法

中图分类号：O422.8                                     文献标识码：A                                  文章编号：1674-957X（2020）24-0073-05

0  引言

车辆NVH（Noise，Vibration，Harshness）是人们一直不断探索的话题，它是评价车辆舒适性的重要指标，好的NVH性能给乘驾人员带来身心的舒适感，而差的NVH性能会严重破坏车室环境，会使驾驶员产生疲劳感，威胁到行车安全[1]。因此，通过优化车室板件降低车室噪声提高车辆NVH性能具有一定意义。

国内外学者对板件优化来降低车室噪声做了大量研究与试验，韩旭[2]面对多场点多声压峰值提出一种新的“声学贡献和”法来分析壁板声学贡献量，全面的衡量板件对多特征点的声学特性的贡献，确定敷设阻尼层的最佳位置，并进行实车试验验证该方法的可行性。赵静[3]通过引入模态置信度准则来验证结构有限元模型的准确性，并计算车内目标点的声学灵敏度曲线，根据实车怠速工况分析车内声压峰值频段下的板件贡献量，在实车上对贡献量大的板件施加阻尼，得到声压峰值明显下降。靳畅[4]引入特征频率计权系数和场点权重系数来分析车内声场的板件贡献量，其中通过1阶模态频率和板件、板件振速、阻尼层厚度间的近似模型等，建立非线性响应面模型。以板件振速最小为优化目标寻求最优组合，通过实车验证优化方案的可行性。Lim T C[5]通过近似光谱公式建立车身板件辐射噪声模型，利用声强和结构声响应的测量装置，得到单面板的贡献函数，通过实车验证该方法的有效性。

本文通过推导封闭空间内板件辐射噪声计算式，分析板件对空间内的声学贡献量，结合目标点位置权重和相对噪声水平系数，提出板件声学在特征频率下的声学贡献量，结合板件声学综合贡献量找出需优化的车身部件。利用最优拉丁超立方设计法对板件厚度参数在空间范围内抽取样本点，并在有限元模型中计算目标响应值，根据输入因子和目标响应利用径向基神经网络法建立近似模型。

1  车辆车身板件声学贡献量分析

车室板件受激励振动形成辐射噪声组成了车室内低频噪声，不同频率下作用在同一板件上的同一目标点下的贡献量各不相同，而同一频率下把不同车身板件贡献量矢量叠加之后作用在声室内任何目标点上形成声压叠加。因此，在对车身板件贡献量的计算分析时，对单一目标点某一频率进行噪声板件贡献量分析不能成为标准，而是需要对车身板件进行综合计算分析得到综合贡献量系数，这样可以精确确定需要优化的车身板件数量。

1.1 封闭结构空间内部声压的计算

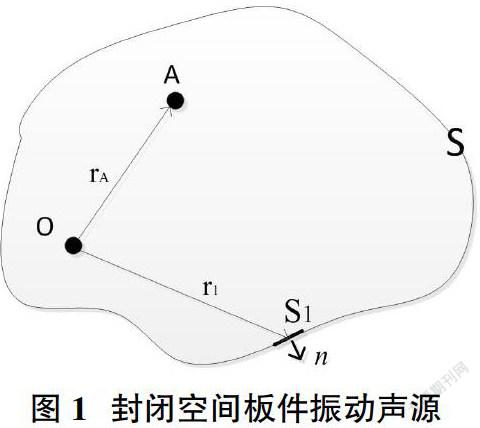
不同车身板件形成的封闭空间组成车室声腔，而形成的声腔是一个不规则的空间形状，如图1所示为封闭空间。

在只考虑壁板声源的情况下，图1为封闭空间是由弹性壁板S组成，O为坐标原点，根据亥姆霍兹积分可知，求解得到辐射噪声。其中解封闭空间车身壁板S以及振动A点所产生的辐射噪声如式（1）所示。

式中G（rA，r1，w）是点体积声源S1对声场中A点辐射声压的格林函数。在测试格林函数时根据互逆原理得到格林函数的另一种表达形式，并對其求导得到式（2）。

式（2）中，QA（rA，w）为A点的体积声源，PS1（r1，w）为S1点的声压。

由声速在n方向导数与声速的关系，以及声压与声速关系，对式（1）进行变换得到式（3）。

在计算声腔内点A的声压时，发现声源A到壁板边缘的速度较低，因此可以忽略不计，即vs1（r1，w）等于0，所以板件辐射在A点产生的声压等于式（3）的第一项。假设车室封闭壁板是由Si（i=1，2…k…n）个点组成，板件上某点对A点的辐射声压如式（4）所示。车身的某块板件L是由S1，S2…Sk个点组成，板件L中某点对车内A点的辐射声压为式（5）。

车身壁板对A点的辐射声压为n个点对A点辐射声压的矢量叠加。则板件L对A点的辐射声压就是板件L内各个点对A点辐射声压的矢量叠加。

1.2 板件综合声学贡献量

通过板件对车内某点辐射声压的量化分析，得出板件L的声学贡献量即是板件L对车内某点辐射声压值在该点总矢量声压值方向上的投影[6，7]。得到板件L对车内A点的贡献量系数为式（6）。

不同板件辐射噪声通过矢量叠加作用在目标点上形成车内声场，因此，在进行板件声学贡献量分析时，需要同时考虑到多个响应点和多个频率等影响因素，而单一条件下计算的板件贡献量不能作为衡量标准，从实际情况考虑，响应点的权重aj，而相对噪声水平系数βj可以通过仿真计算得到，从而获得多响应点多频率下车身板件综合贡献量系数，即：

其中，s响应点的个数，m特定频率的个数，Dej（ωi）某频率下车身板件对于响应点的贡献量系数。

1.3 车身板件声学贡献量计算

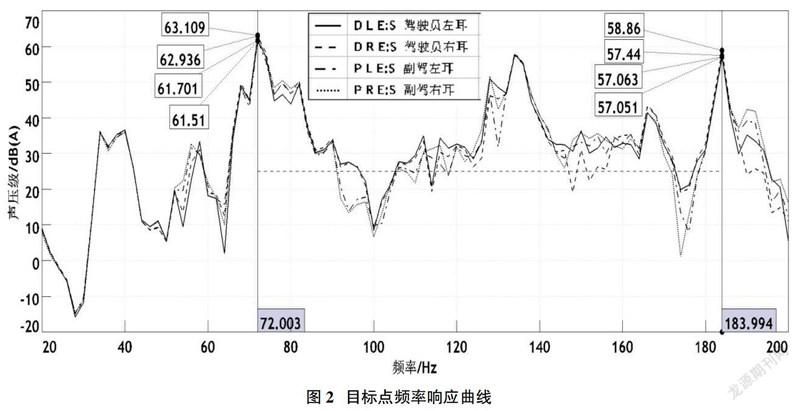
建立整车声-固耦合有限元模型，通过对比有限元法与理论法计算车身结构局部模态频率，验证所建结构模型的准确性。利用LMS Test.Lab试验台测量发动机悬置点激励数据，选取频段20～200Hz的激励载荷，在Virtual.Lab中对车身结构悬置点施加该载荷，运用耦合边界元法计算车室噪声[8-9]，选取驾驶员与副驾双耳位置为目标点，得到四个目标点的声压曲线如图2所示。

图2中可知四条频率响应曲线的波动趋势基本一致，其中所对应的曲线分别为驾驶员左耳（DLE）、驾驶员右耳（DRE）、副驾左耳（PLE）以及副驾右耳（PRE），通过对频率响应曲线的研究，其中72Hz、134Hz和184Hz作为突出峰值，而在频率72Hz处，四个目标点的声压值都在62dB处波动，在频率134Hz处四个目标点的声压值在57dB处波动，在频率184Hz处四个目标点的声压值在57dB处波动。声场内各板件产生的噪声相互耦合使得频响曲线的趋势出现波动，其中声压峰值，可能是由于板件强烈辐射造成或由于声腔共鸣引起。

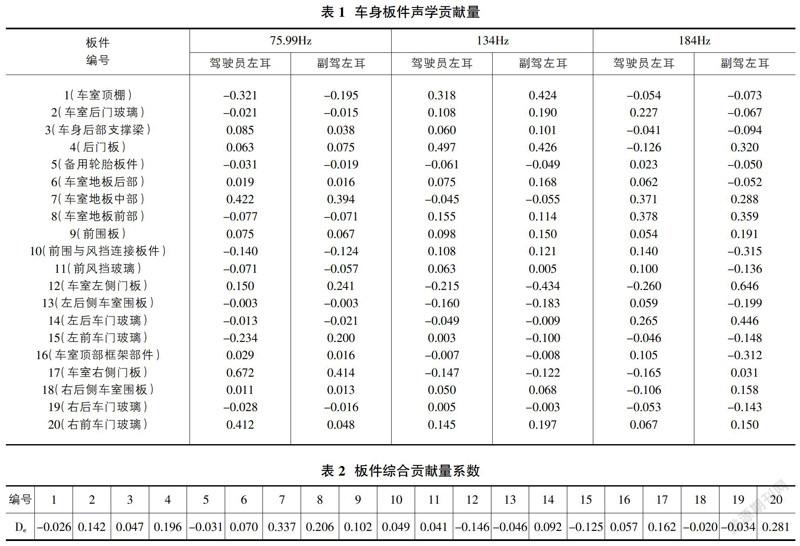
通过对声压峰值频段的确定，由此可以得到峰值频段下车身板件的声学贡献量，通过声腔与车身结构耦合边界面，可以把车身板件分割为20块区域，结合在Virtual.Lab中计算特征频率下结构耦合板件贡献量的计算公式，得到了在不同目标点上的声学贡献量系数如表1所示。

从表1中得出同一板件对同目标点在不同频率下，贡献量是不相同的，根据公式（7）可得车身板件综合贡献量系数如表2，根据车室乘坐工况，设定驾驶员位置权重系数为1，副驾位子为0.6，通过公式（8）计算噪声水平系数得到驾驶员左耳位置的噪声水平系数0.502，副驾系数为0.498。因此，计算得到板件综合贡献量系数如表2所示。

由表2可知，7号、20号、8号、4号、17号、2号、9号为综合贡献量较大的车身板件位置，把需优化板件分别记作X1、X2、X3、X4、X5、X6、X7。

2  建立板件厚度参数与目标响应间的近似模型

2.1 空间样本点数据采集

通过表2得到综合贡献量较大的板件位置，其中把7块板件厚度参数作为设计因子，并且通过车门玻璃和车身板件的国家标准确定7个设计因子的取值范围，具体取值范围为：X2和X6的取值在2.5～4mm，剩余5块板件设计因子取值为：0.5～2mm。

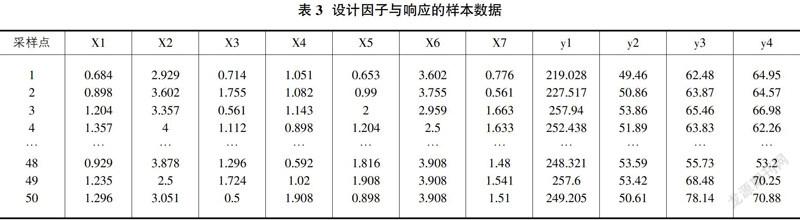
采用最优拉丁超立方采样法在Isight中对7个设计因子在空间上抽取50组样本点，得到50组随机水平组合。通过整车模态分析，在车身模态第17阶出现了整车一阶扭转模态，所以y2记作第17阶模态频率响应，其中车身质量y1、驾驶员左耳和副驾左耳声压均方根值分别为y2、y4。根据50组设计因子使用有限元法计算输出响应的50组参数，得到输入因子与输出响应的50组水平组合如表3所示。

2.2 近似模型的建立与误差分析

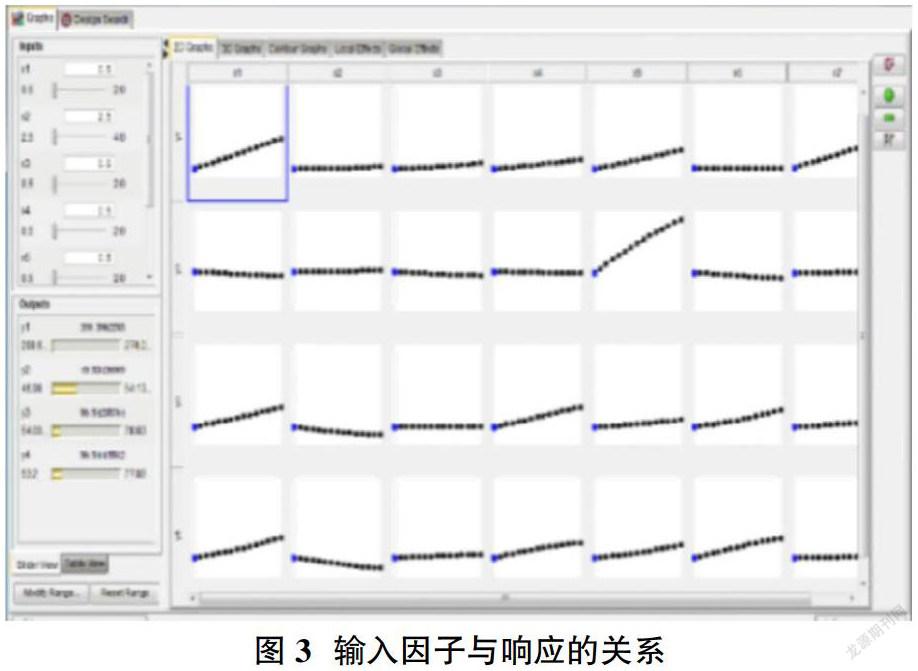
通过表3的50组数据，利用RBF建立起设计因子与目标响应的近似模型。采用径向基神经网络模型，在Isight中把7块板件厚度参数设定为输入因子，而四个目标值设定为响应，得到输入因子与响应关系的近似模型如图3所示。

图3中显示出每个变量因子对目标响应的影响趋势，观察可知X1的变化对y1有强烈影响;X5的变化对y2有强烈影响，其余变量因子对目标响应y1和y2的影响相对平稳。y3和y4相对于每个变量因子变化趋势较大，说明输入因子的波动对其影响较大。

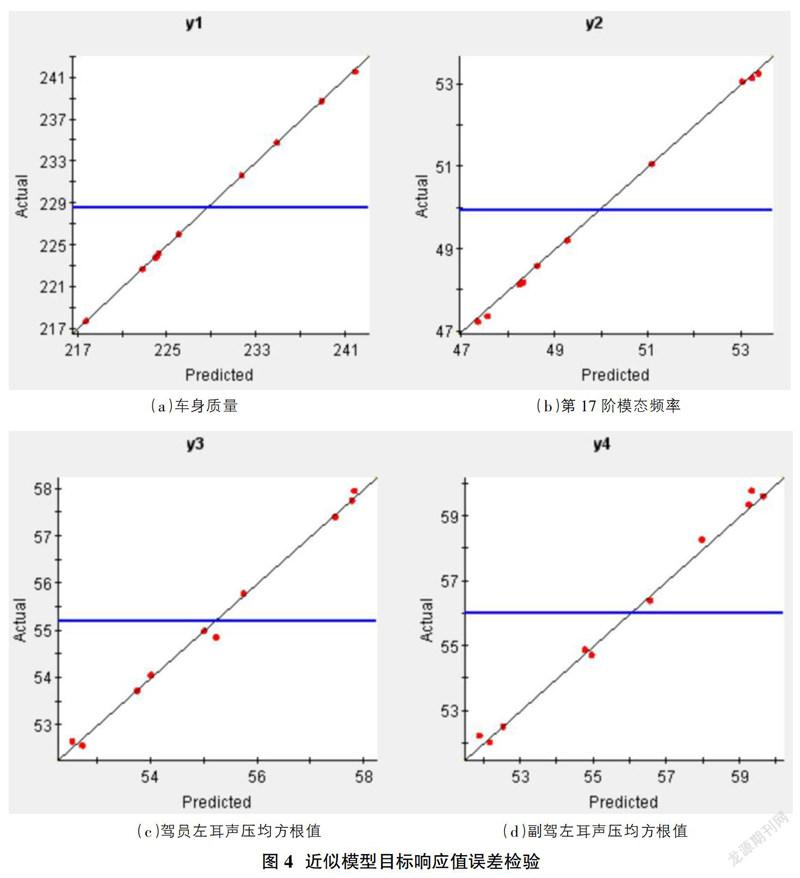
为了检验所建模型的精确度，通过随机抽取样本的方式进行验证，在设计矩阵中选取10组样本数据进行分析，得到结果如图4所示。

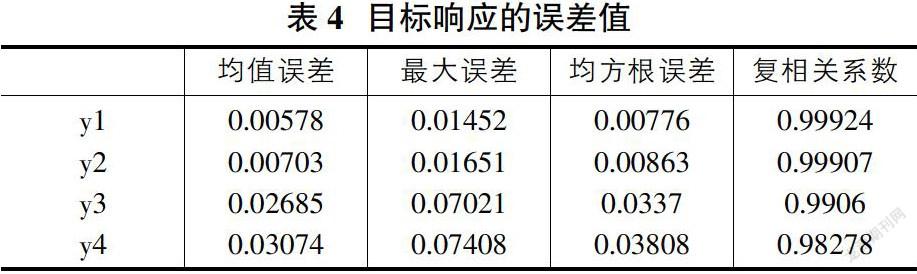
由图4可知，车身质量图4（a）和车身第17阶模态频率图4（b）的样本点的分布情况可知，其样本点基本都落在近似模型的直线上。驾驶员左耳声压均方根值图4（c）与副驾左耳声压均方根值图4（d）这两者大部分点落在直线上或近似模型直线附近，因此，近似模型与数据很好的吻合，证明了近似模型较的精度，以均值误差、均方根误、最大误差附相关系数这四个指标来评价近似模型的准确性，其中均值误差和均方根值误差的上限为0.2，这两者值越小越好，最大误差值也要求越小越好上限为0.3，复相关系数R2的值越大越好其上限为0.9。计算这四个指标的具体数值如表4所示。

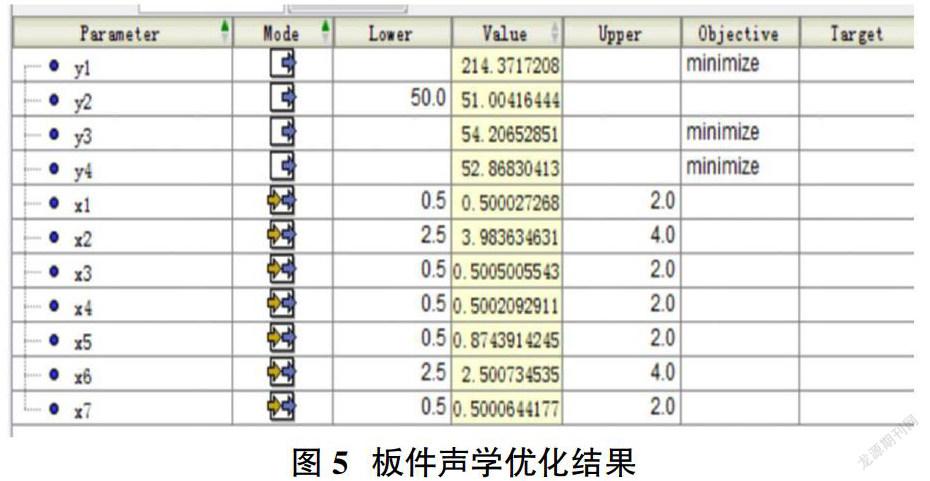
表4中四个响应值的指标值都远小于其上限，并且复相关系数值接近1，说明所建立的四个响应与输入因子间的近似模型具有很好的拟合性。在Isight中选用NSGA-II算法，选定种群规模为100，世代数160，交叉概率0.9，交叉分布指数10，突变分布指数为20，经过16001次计算在14168处得到最优结果，计算得到结果如图5所示。

通过有限元模型计算，验证车身板件近似模型的优化结果较为准确，如图5所示。

3  结论

①通过板件振动辐射理论计算空腔内目标点辐射噪声并推导板件声学贡献量，结合目标点位置权重与噪声水平系数得到板件声学综合贡献量。通过有限元法计算车室目标点的频响曲线，在结合车身结构划分出20块车身板件，计算得到目标点声压峰值频段下板件声学贡献量系数，根据板件声学综合贡献量系数计算得到需优化的板件为车室地板中部、车室右侧门板、车室后门玻璃、车身前围板、右前车门玻璃、车内板前部、车身后门板。

②通过对7个设计因子经过最优拉丁超立方设计法在空间范围内随机抽取50组数据。根据输入因子与输出响应，通过径向基神经网络模型建立近似模型。并且随机抽取10组数据对其进行性进行误差分析，得到建立的近似模型具有较高精度，可以作为原方程的简化方程來进行优化设计作为参考。

参考文献：

[1]付吉云.基于声固耦合模型的轻型客车车内低频噪声分析与控制[D].2016.

[2]韩旭，余海东，郭永进，等.基于壁板声学贡献分析的轿车乘员室声场降噪研究[J].上海交通大学学报，2008，42（8）：1254-1258.

[3]赵静，周鋐，梁映珍，等.车身板件振动声学贡献分析与优化[J].机械工程学报，2010，46（24）：96-100.

[4]靳畅，周鋐.基于车内综合声场贡献分析的车身板件声振优化[J].汽车工程，2015，37（12）：1438-1444.

[5]Lim T C . Automotive panel noise contribution modeling based on finite element and measured structural-acoustic spectra[J]. Applied Acoustics， 2000， 60（4）：505-519.

[6]白松，徐新喜，刘孝辉，等.车辆壁板声学贡献分析与降噪试验研究[J].振动与冲击，2013，32（24）：204-208.

[7]张志勇，张义波，刘鑫，等.重型卡车驾驶室结构噪声预测与板件声学贡献度分析[J].振动与冲击，2014，33（13）：67-71.

[8]王二兵，周鋐，徐刚，等.基于车身板件声学贡献分析的声振优化[J].江苏大学学报（自然科学版），2012，33（1）：25-29.

[9]张一麟，廖毅，莫品西，等.基于车身模态和板块贡献分析的阻尼优化降噪方法研究[J].振动与冲击，2015，34（4）：153-157.

[10]侯献军，郭金，杜松泽，等.基于声模态和板件贡献分析的车身降噪研究[J].汽车技术，2018，512（05）：44-48.