对霍尔效应实验系统误差的探究

魏国荣 薄永红

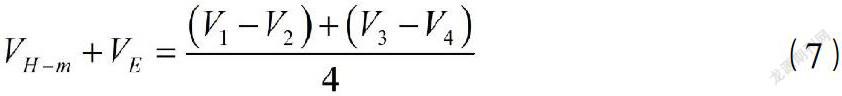
摘要：内燃机车电传动控制电路的检测速度和有效性，直接影响到内燃机运行的可靠性。本文介绍的霍尔效应实验系统误差研究，从理论上讲测量霍尔电压系统误差主要是由于爱廷豪森效应、能斯脱效应、里纪-勒杜克效应和不等位电势差四个副效引起的，本文在对称法和交流法两种测量方法的基础上，推导出测量计算公式，并通过测量数据做了相对误差计算和分析，说明了它们的影响程度。

关键词：霍尔效应;爱廷豪森效应;能斯脱效应;里纪-勒杜克效应

中图分类号：O4-34                                      文献标识码：A                                  文章编号：1674-957X（2020）24-0001-04

0  引言

内燃机车电传动控制电路故障检测及自动处理，可以快速故障定位、自动应急处理，消除行车隐患，维持机车内燃机正常运行。在内燃机车电气系统的控制特点布线十分复杂，可靠性差，部分触头因裸露结构，容易发生因落灰后接触电阻过大，发生虚接、开路等故障。机车运用过程中发生电器联锁故障后查找判断困难，给行车组织带来较大影响。本文研究的霍尔效应实验方法，是高校理工科基本实验之一，无论是作为普通物理实验[1]还是近代物理实验[2]测量霍尔片的霍尔电压是实验的关键。

由于在霍尔效应中，还伴随着爱廷豪森效应、能斯脱效应、里纪-勒杜克效应和不等位电势差等副效应，这些副效應对霍尔电压的测量带来系统误差。在实验室里，消除这些系统误差常用的方法是用对称法，即通过换向器来改变通过霍尔片的工作电流方向和磁感应强度方向。霍尔效应已在自动化技术、测量技术、智慧城市建设和人工智能等领域里有十分重要的应用。而在实际使用中，不可能像实验室里采用一些方法来消除这些副效应的影响，要减小或消除它们的影响，可以从两方面着手，一是在制造方面，应提高制造工艺水平;二是在使用方面，应设计附带电路，加以修正。要做到这两点，知道这四个副效应产生的系统误差变的十分重要。本方拟对霍尔效应中，各副效应引起的电压对霍尔电压测量产生的系统误差进行理论和实验方面的研究，推导出它们误差的计算公式，并通过实验测量数据计算出它们的误差，说明它们的影响程度。

1  回顾理论

1.1 霍尔效应公式[1]

式中VH为霍尔电压，KH为霍尔片的灵敏度，它反映产生霍尔电压的能力，单位为mV·mA-1·T-1，Is是通过霍尔片的工作电流，B是垂直穿过霍尔片磁场的磁感应强度。

从式（1）中看出，霍尔电压的大小与工作电流和磁感应强度的乘积成正比，其方向与工作电流和磁感应强度的方向均有关系，当工作电流和磁感应强度的方向改变时，霍尔电压的方向均要改变。

1.2 爱廷豪森效应

在霍尔效应中，爱廷豪森效应产生的电压与工作电流和磁感应强度之间的关系式为[2]：

式中VE是爱廷豪森效应产生的电压，其值与工作电流和磁感应强度的乘积成正比，而方向和霍尔电压一样，与工作电流和磁感应强度的方向均有关系。

1.3 能斯脱效应

在霍尔效应中，能斯脱效应产生电压的关系式为[2]：

式中VN是能斯脱效应产生电压，Q是由于霍尔片两端连接工作电流的电极触点电阻有差异，当电流通过霍尔片时，由于焦耳热不同，使霍尔片两端有温度差，产生的热流，其流向与触点电阻值差异有关，而与工作电流方向无关。可见，能斯脱效应产生电压的方向仅与磁感应强度方向有关，而与工作电流方向无关。

1.4 里纪-勒杜克效应

在霍尔效应中，里纪-勒杜克效应产生电压的关系式为[2]：

由此可见，里纪-勒杜克效应引起的电压VRL的方向与能斯脱效应一样，仅与磁感应强度的方向有关，而与通过霍尔片的工作电流方向无关。

1.5 不等位电势差

不等位电势差是由于霍尔片将霍尔电压输出的电极非完全相对应和霍尔片本身纯度及形体不均匀等因素导致的，这与制作工艺有关，其大小还与工作电流Is的大小有关，若给霍尔电压输出的两电极间的纵向一个电阻值Rd，则根据欧姆理论，不等位电势差Vd为：

可见，不等位电势差Vd仅与工作电流Is有关，而与磁场无关，其电压方向随工作电流方向的改变而改变。

2  系统误差计算公式

2.1 测量方法

2.1.1 对称法

从式（2）、式（3）、式（4）中看到，能斯脱效应、里纪-勒杜克效应和不等位电势差产生电压的方向或与工作电流方向有关，或与磁感应强度方向有关，而霍尔电压的方向与工作电流和磁感应强度的方向均有关系，故在实验室里，常采用改变工作电流和磁感应强度方向（实验中用改变励磁电流的方向来改变磁感应强度方向的），来消除它们影响的（忽略爱廷豪森效应的影响），这种方法把它称之为“对称法”，分析过程如下。

根据式（1）、式（3）、式（4）和式（5）得：

可见，采用对称法测量，霍尔电压的测量值VH-m用下式：

来计算，这样就消除了能斯脱效应、里纪-勒杜克效应和不等位电势差对霍尔效应的影响。

需要说明的是，用式（6）计算结果若是正值，表明霍尔电压的实际方向与假设方向相同，若是负值，表明霍尔电压的实际方向与假设方向相反。

2.1.2 交流法

由式（1）和式（2）看到，爱廷豪森效应产生的电压VE与霍尔电压VH一样，均与通过霍尔片的工作电流和垂直穿过霍尔片的磁感应强度乘积成正比，当工作电流和磁感应强度的方向改变时，爱廷豪森效应产生的电压和霍尔电压的方向均要改变，若考虑到爱廷豪森效应的影响，测量霍尔电压的计算式（6），应变更为：

所以不能采用对称法来消除爱廷豪森效应对霍尔效应的影响。

由于霍尔效应的建立所用时间很短（大约在10-14～10-12秒内[3]），而稳定的温度差的建立需要时间较长（约几秒[2]），所以只要通过霍尔片的工作电流用交流电即可，例用0.02秒的工频电流，在0.01秒内，霍尔效应已十分稳定，而温度差还没有建立，电流方向就开始反向了，这样就基本保证了霍尔片上下两侧温度的均匀，消除了爱廷豪森效应对霍尔电压的影响，当然此时的霍尔电压也是交变的，应用交流电压表来测量。

从式（3）看到，能斯脱效应由热流引起，而热流与工作电流方向无关，所以虽然工作电流是交流电，能斯脱效应产生的电压仍是直流电压，它的方向仅随磁场方向的改变而改变，用交流电压表测量时，它对交流电压表的示数没有贡献。

同样，里纪-勒杜克效应也是由热流引起，所以里纪-勒杜克效应引起的电压同样是的直流电压，用交流电压表测量时，它对交流电压表的示数同样没有贡献。

但是，当工作电流用交流电时，根据式（5）看出，不等位电位差也是交流电压，所以，它已不能用改变磁场方向的方法来消除它的影响，由于不等位电位差的大小与磁场的磁感应强度大小无关，所以实验中可以使磁场的磁感应强度取零（断开励磁电流的开关）时，霍尔电压已经变为零，所以测得的电压值就是不等位电位差。

综上所述，当工作电流用交流电时，并不需要换方向，测二次就行了，比用直流电来测量简单，具体方法如下：

①当磁感应强度B≠0时，有：

式中，不等位电位差Ud取向有正负之分，若Ud和UH是同相位，应取正;若Ud和UH是反相位，应取负。实验中要知道它们是同相位还是反相位，要等在对称法测量中，计算出的不等位电位差Vd-m与霍尔电压VH-m是同向还是反向才能确定。

②当磁感应强度B=0时，有：

显然，霍尔电压的测量值为：

式中正负号的选取和上面的道理是一样的，它们若同相位，应取负，反之取正。

2.2  误差计算公式

2.2.1 能斯脱效应、里纪-勒杜克效应的误差计算

根据对称法测量，因为：

可见在对称法测量中，计算能斯脱效应与里纪-勒杜克效应产生的电压值之和计算式为：

式中，若计算结果是正值，表明能斯脱效应与里纪-勒杜克效应电压之和的实际方向与假设方向相同，若是负值，表明电压的实际方向与假设方向相反。

与霍尔电压相比，产生的相对误差为

2.2.2 不等位电势差的误差计算

根据对称法测量，因为：

可见在对称法测量中，计算不等位电势差的计算式为：

同样，计算结果若是正值，表明不等位电势差的实际方向与假设方向相同，若是负值，表明不等位电势差的实际方向与假设方向相反。

与霍尔电压相比，产生的相对误差为：

在交流法中，不等位电势差的相对误差计算要简单得多，计算式为：

2.2.3 爱廷豪森效应的误差计算

对爱廷豪森效应引起的误差只能做粗略的估算，在工作电流用交流电时，若在交流电流的有效值与对称法的直流电流相等，且磁场的感应强度也相等的情况下，根据式（7）和（8）可得：

其相對误差为：

3  样品系统误差计算及分析

在实验室里，笔者用了TH-S型螺线管磁场实验仪和TH-S型螺线管磁场测试仪（浙江天煌科技实业有限公司研制），对两个样品进行测量，限于篇幅，仅用一例。

3.1 测量数据及误差计算

测试样品：灵敏度为2.54mV·mA-1GS-1的硅晶片，螺线管匝数密度为111.70×102·m-1。

测量数据为表1和表2。

表1中，VH-m表示霍尔电压的测量值，正值表示实际值方向与假定方向相同，若是负值表示实际值方向与假定方向相反（下同），VNRL-m表示能斯脱效应与里纪-勒杜克效应。

表2中，UH-m表示用交流法测得的霍尔电压有效值，VE-m表示爱廷豪森效应引起电压的测量值，EE表示其引起的相对误差。

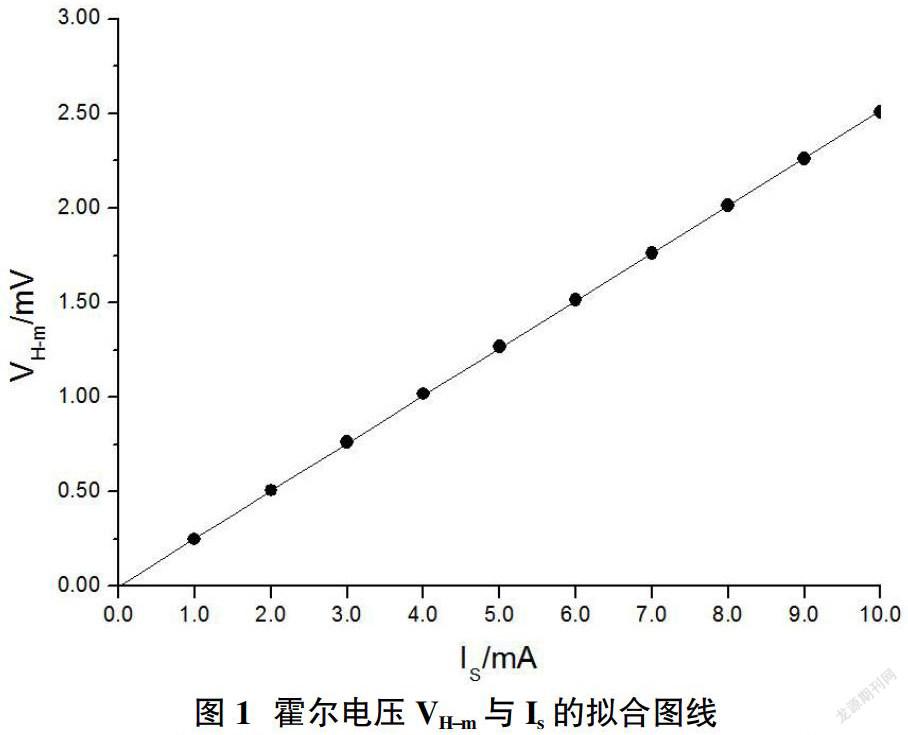
3.2分析图表（图1）

里纪-勒杜克效应产生的电压值之和的测量值，ENRL表示其相对误差，Vdm表示不等位电势差的测量值，Ed表示其相对误差。

笔者对两个样品用Origin工具绘制了霍尔电压与工作电流间的拟合图线，线性关系都比较理想，并发现它们均与霍尔电压坐标轴有一很小的负向截距，该截距就是爱廷豪森效应引起电压值，同时也表明测量数据是比较理想的。（图2、图3）

图表中，不等位电势差的测量值用了绝对值。

3.3 系统误差分析

3.3.1 不等位电势差及误差

根据表1和表2的比较看到，在这四个副效应中，不等位电势差最大，其量级与霍尔电压基本是同级别的，所以测量仪器能较好的分辨出来，图3表明，它较好的反映了与工作电流正比关系的理论值，也就验证了关系式（5）是成立的。

不等位电势差产生的相对误差也最大，该样品的平均相对误差值达17.61%，另一样品的平均相对误差值也达8.77%。

3.3.2 爱廷豪森效应及误差

爱廷豪森效应产生的电压与不等位电势差相比要小些，但其量级与不等位电势差的量级相比差得不大，所以测量仪器也能较好的分辨出来，图2表明，它也较好的反映了与工作电流正比关系的理论值，基本验证了关系式（2）是成立的。

爱廷豪森效应平均相对误差值该样品为3.35%，另一样品为2.78%，与其它文献在5%以下的结论相符。

3.3.3 能斯脱效应与里纪-勒杜克效应及误差

能斯脱效应与里纪-勒杜克效应产生电压之和极小，是微伏量级，大约是不等位电势差的千分之几。若把前两次测量误差剔除后（由于电压很小，测量仪器精度较低，仪器误差影响较大），其平均相对误差值该样品为0.08%，另一样品为0.05%。可见能斯脱效应和里纪-勒杜克效应对霍尔效应的影响极小，可以忽略不计。究其原因，是由于连接硅晶片两端电极的接触电阻极小（面结合），其差异更小，因而产生的焦耳热极小，温度差更小，且温度差的建立要几秒时间，它又不断向周围散发热量，故在晶片里的热流极小，其扩散电流极其微弱，大约是微安量级，它所产生的霍尔电压（即能斯脱效应）是微伏量级，而里纪-勒杜克效应实际上是扩散电流产生的爱廷豪森效应，它的量级更小，是能斯脱效应的百分之几，且通过分析，其极性与能斯脱效应的极性相反，因而这两种效应之和对霍尔效应产生的影响极其微弱.在实验测量中，由于能斯脱效应和里纪-勒杜克效应产生的电压极其微弱，比测量仪表（读到0.01毫伏）要小很多，故仪表显示读数的随机性和外部环境的偶然性等因素反而起了主要作用，所以其测量值有时为正、有时为负就感到不奇怪了。

4  结语

上面定量讨论了在实验室里用对称法求能斯脱效应与里纪-勒杜克效应产生电压之和和不等位电势差产生电压的测量计算式，结合交流法求爱廷豪森效应产生电压的测量计算式，其测量计算式（9）、式（11）和式（14）是本文最重要的理论成果。

测量分析图线表明，不等位电势差的测量值与理论值相符性非常好，爱廷豪森效应产生电压的测量值与理论值相符性也较好。

通过实验测量表明，在霍尔效应中，不等位电势差最大，其量级与霍尔电压几乎相当，产生的相对误差较大，达百分之几到几十，其次是爱廷豪森效应，其相对误差也达百分之几，能斯脱效应和里纪-勒杜克效应产生的电压极其微弱，只有霍尔电压的万分之几，一般仪器无法分辨，所以其值在零点上下随机波动，可以忽略不计。上面两点是本文最重要的实验成果。

由于霍尔晶片在实际使用中，不能像实验室里那样用对称法或交流法来消除副效应的部分影响。根据在霍尔效应中，不等位电势差的影响最大，其次是爱廷豪森效应，造成的原因主要是霍尔晶片的制造工艺水平，所以在制造时应注意晶体杂质分布的均匀性、材料密度的一致性、體形的规则性和引出电极的对称性;在实际使用时，主要对已存在的影响用附加电路加以修正，以消除它们的影响，例可以用集成运算电路作为修正电路。这是本文在研究结论基础上对制造工艺和实际使用中的两点建议。

参考文献：

[1]吴锋，李端勇.大学物理实验-基本篇[M].二版.北京：科学出版社，2009：152-157.

[2]吴思成，王祖铨.近代物理实验[M].北京：高等教育出版社，2005：402-412.

[3]刘昶丁，柳纪虎.用交流方法削去霍尔效应中的副效应影响问题的探讨[J].半导体技术，1987，14（1）：49-52.