基于APOS理论下“弧度制”的教学设计

摘 要：数学概念是建构数学理论大厦的基石，是学生认知的基础，进行数学思维的起点，也是数学抽象的一个重要表现，概念教学在数学教学中具有举足轻重的地位。APOS理论是美国数学家杜宾斯对数学概念的学习提出的理论。本文结合APOS理论，以必修4弧度制的概念教学为例，探讨在实际教学中如何凸显概念的本质，实现核心素养的培育，提高高中数学概念教学的有效性。

关键词：APOS理论;概念教学;弧度制;教学设计

一、APOS理论概述

上世纪60年代，美国数学家、教育学家杜宾斯基等人提出了APOS理论，该理论是对皮亚杰“自反性抽象”的延伸和拓展。杜宾斯基认为，在数学概念的学习中，如果个体经过思维的操作、过程和对象等几个阶段后，一般就能在建构和反思的基础上，把它们组织成用以解决问题情境的图式结构[1]。APOS理论主要包括Action（活动）、Process（过程）、Object（对象）和Scheme（图式）四个过程。

1、第一阶段——活动（Action）阶段

“活动”阶段是指学习者通过一系列的操作活动初步认识数学对象。教师利用学生熟悉的生活实例创设情境，让学生通过观察、运算、实验、类比、猜想、判断等一系列活动建构知识。这一阶段为数学概念的初步形成打好基础，是学生建构数学概念的起点，是完善数学概念的前提基础。

2、第二阶段——过程（Process）阶段

“过程”阶段是概念学习的关键，是学习者对前面活动的进一步思考，是对“活动”阶段的抽象概括。在外在的实际活动和内在的思维操作之后，学生逐步认识到数学概念的本质，并对概念进行一般化的概括，是确立数学概念的必要准备，也是学生概念学习的关键阶段。

3、第三阶段——对象（Object）阶段

“对象”阶段是指学习者对前面两个阶段的活动进行深入地思考，归纳和概括出数学概念的本质属性，用相对严谨的文字语言描述这一属性[2]，并进行数学符号化表示，成为一个具体的对象，并能够将其作为新的数学对象参与到其他数学问题的研究过程。

4、第四阶段——图式（Schema）阶段

经过前三个阶段，概念此时作为数学对象，与之相关的其他数学概念进行整合形成新的认知结构和知识网络，就是“图式”阶段。这一阶段是对概念进行综合的心理加工和整合，在概念间形成实质性的联系，建立新的认知结构，使学生对概念的认识逐渐深化，在长期的数学学习活动中逐渐体现。

二、基于APOS理论的弧度制概念教学设计

（一）教学分析

弧度制的概念是三角函数的重要概念之一，是学生学习三角函数的基础。由必修一中函数的定义可知，函数是两个非空数集之间的对应。而在初中所学的三角函数自变量是角，这与学生现有的知识产生了矛盾，而弧度制的定义方式则是完美的实现了角和实数之间的一一对应，有效的解决了这一认知冲突。然而，教材中对于弧度制的介绍却十分简单，只是通过类比引出弧度制，给出1弧度的定义。教师在教学时也只是将弧度制作为工具性知识，一笔带过，这都是造成学生对弧度制概念理解有困难的原因。基于此，利用杜宾斯基的APOS理论对弧度制的教学做如下设计。

教学目标：

（1）经历弧度制概念的形成过程，理解弧度的意义，并能正确进行弧度与角度的换算;

（2）了解角的集合与实数集之间的一一对应关系;

（3）从初中角度制的弧长与扇形的面积公式，推算出弧度制下的弧长与扇形的面积公式，解决简单的实际问题

教学重点：弧度制的定义，弧度制与角度制的换算

教学难点：学习弧度制的必要性，正确理解弧度制的意义

（二）教学过程

1、活动阶段——情景引入，形成直观认识

在扳手拧紧螺帽的过程中，扳手的转动与螺帽的转动之间有什么联系？

教师提示：将实际生活情景抽象成数学问题，螺帽从A1转到到B1，扳手的另一端从点A转动到点B，在这个过程中，几何数量之间具有哪些相等和不等关系？

学生活动：因为扳手转动的弧长更大，所以点A转动的弧长与点A1转动的弧长不相等，两弧所在圆的半径也不相等，但点A和点A1转动的角度相等。

设計意图利用学生熟悉的生活场景引入，引导学生用数学的眼光观察世界。扳手拧紧螺帽是学生熟悉的生活体验，但其中蕴含的“弧长与半径比值为定值”的数学元素，是陌生的、抽象的，该阶段主要让学生初步感受到弧度制度量角的合理性。

2、过程阶段——提问设疑，抽象概念本质

问题1上图中扇形A1OB1与扇形AOB相似，即你能证明吗？

学生活动：根据初中学过的弧长公式（其中n是圆心角的角度数）。在扇形A1OB1中，;在扇形AOB中，，所以。

教师活动：在上述证明中，我们不仅可以得到，还发现，即只与角的大小有关，当角α确定，也是唯一确定的。

设计意图对于弧度制这节课，大多数是通过其他单位制中，例如长度可以用“厘米”“米”“千米”来度量，进而引入角的新的度量方式——弧度制。这样的引入并不能使学生真正认识到弧度制的作用，只是简单的将其看做是角的另一种度量形式，就是数学中的一种规定。上述教学设计则是依托具体数学问题，让学生经历自主探究、猜想、求证等过程，认识到为什么要这样规定，以及这么规定的合理性，让学生理解弧度制的本质。

3、对象阶段——探究反思，建构数学概念

问题2用α=度量角，角的单位是什么？

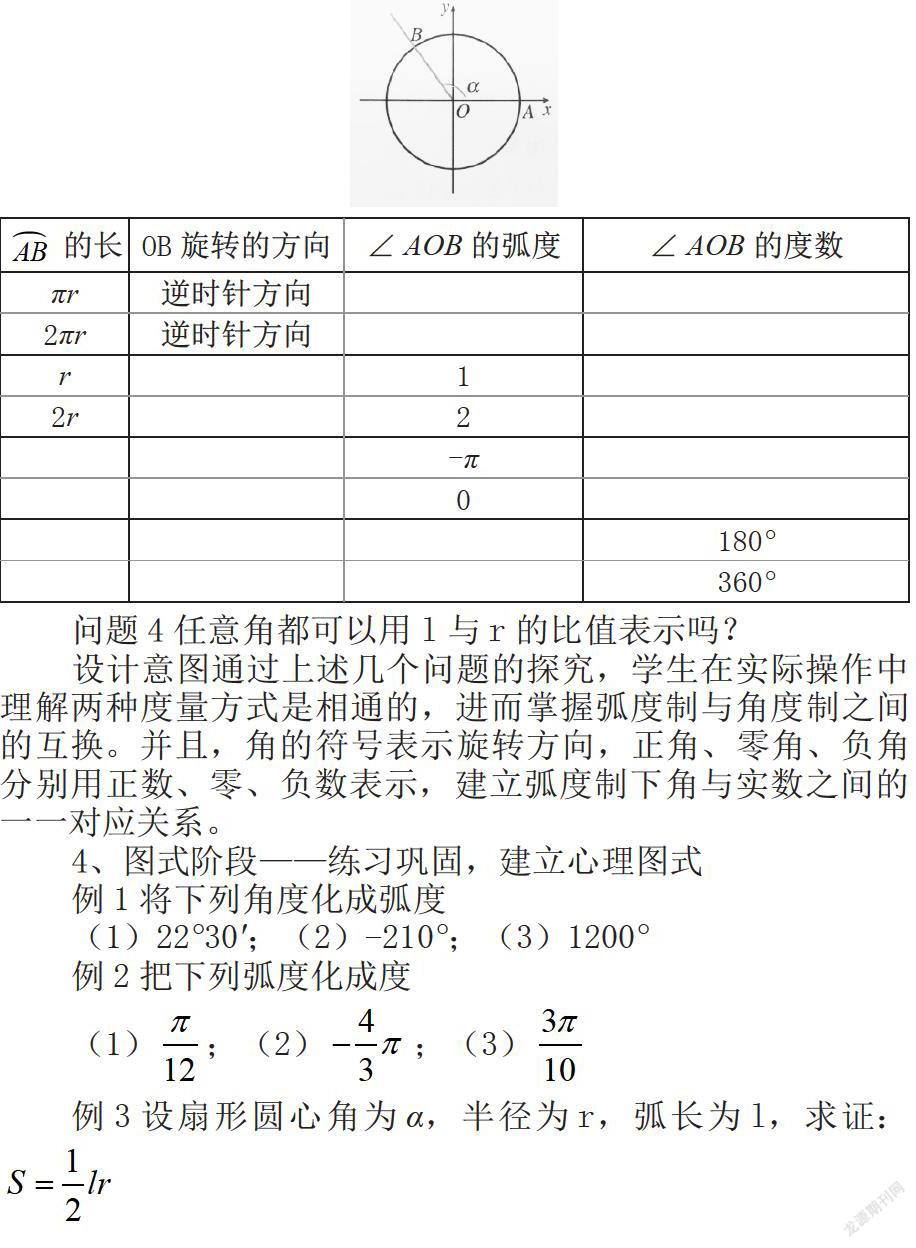
问题3角度制、弧度制都是角的度量制，它们之间如何换算？分组探究并完成下表

问题4任意角都可以用l与r的比值表示吗？

设计意图通过上述几个问题的探究，学生在实际操作中理解两种度量方式是相通的，进而掌握弧度制与角度制之间的互换。并且，角的符号表示旋转方向，正角、零角、负角分别用正数、零、负数表示，建立弧度制下角与实数之间的一一对应关系。

4、图式阶段——练习巩固，建立心理图式

例4已知扇形的周长为10，圆心角为3rad，求该扇形的面积

问题5通过本节课你学到了哪些知识？

设计意图学生经过前面三个阶段的学习后，基本建立了如下的心理图示：弧度制是用弧长和半径来度量角的一种方式，弧度制与角度制之间可以互相转换，弧度制实现了实数与角之间的一一对应关系等。通过上述例题，巩固学生对弧度制的认识，正确地进行弧度与角度之间的换算，掌握弧度制下的弧长和扇形面积公式，利用弧度制解决某些简单的实际问题。最后由学生总结本节课的知识点，并与原有的图式进行整合，建立起综合的心理图式。

三、结束语

APOS教学理论强调，学习需要学生主动建构，在“操作阶段”感知数学、在“过程阶段”抽象数学概念、在“对象阶段”归纳数学本质、在“图式阶段”建构知识体系。这四个阶段也与数学核心素养密切相关：弧度制概念的建立，经历了从实际生活抽象出研究对象的过程，以问题激发学生的求知欲，促进学生主观思考与推理，其中也有一些直观思维的参与，这都吻合数学学科核心素养中的数学抽象、逻辑推理、直观想象。

总之，APOS理论对数学概念教学具有很好的指导意义，要实现课堂教学从“灌输”到“建构”的转变，需要教师更多的设计与探究，让学生真正成为学习的主人。

参考文献

[1]周继云.基于APOS理论的初中函数教学研究[D].苏州：苏州大学，2010.

[2]李琛.基于APOS理论下的对数概念教学现状探究[D].西安：陕西师范大学，2018

作者简介：李若璕（1993年2月，女，籍贯江西抚州，福建省厦门实验中学，中学二级，华中师范大学，学科教学（数学）专业，硕士学位，研究方向数学学科教学）