大型复杂构件的无模型工业机器人自动编程系统

侯润石 蒋启祥 王胜华 魏秀权

摘要：航空、航天、船舶制造等领域存在着大量缺少计算机几何模型的小批量、柔性化构件焊接制造需求，基于模型的离线自动编程系统难以适用。就此设计了一种无模型大型复杂构件机器人自动编程系统。该系统通过对待加工构件进行快速三维重建，分析三维重建结果，预先规划加工方案，并自动生成机器人程序，通过传感器测量几何模型与实际构件之间的偏差，在线修正机器人程序。结果表明，系统能够对缺少模型的大型复杂构件进行在线分析，无需工作夹具的辅助便能有效地完成相应的焊接任务，为机器人加工进一步自动化提供了技术基础。

关键词：无模型构件;三维重建;自动编程;在线修正

中图分类号：TP24 文献标志码：A 文章编号：1001-2303（2020）07-0134-07

DOI：10.7512/j.issn.1001-2303.2020.07.21

0 前言

工业机器人因具有通过再编程以适应工作环境变化的特性，在智能制造中占有重要地位。传统的工业机器人程序编制一般通过人工参与的在线示教方式来实现，具有编制周期长、示教精度低、复杂轨迹实现困难的缺点[1]。在面对航空、航天、船舶制造等领域所存在的小批量、多品种、复杂构件焊接制造需求时，因人工示教编程的时间和经济成本远大于人工建造的时间和经济成本，工业机器人往往难以得到有效的应用。因此，研究机器人自动编程系统对于以工业机器人为重要基础的智能制造技术的推广具有重大意义。

基于数字化几何模型的离线编程方式是近年来发展较快且较为成熟的一种自动编程方案[2-5]，该方式通过人工交互在已有的数字化几何模型基础上进行规划并自动生成机器人程序。由于待加工构件与编程环境下的构件往往存在位置误差，所以此方案多应用于对位置误差要求并不严格的领域，如喷涂、切割和折弯等[6-12]，或者通过工装夹具来保障位置误差处于合理范围内。但工装夹具也难以应用在待加工构件难以移动的场合。为克服这一困难，研究者通过检测待加工构件的位置，然后对原模型数據进行标定后重新编程，或者依据待加工构件位置的检测结果校正生成的程序。较为典型的有YASKAWA的始端检出设计[13]、以及荷兰的KraneDock公司设计的一系列非重复性机器人加工系统。该方法仍然要求具有与实际构件精确对应的数字化模型。上述各种方法均实现了机器人程序的自动编制，提高了作业规划的效率，促进基于工业机器人的智能制造技术在非重复性制造领域的推广。但以上方法均要求有预先设计好的与构件本身精确对应的几何模型，而在钢结构及造船等行业中，许多构件的焊接制造缺少事先设计好的几何模型，上述方法难以胜任。

文中针对缺少几何模型构件的焊接制造需求，设计了一种可在线三维重建获取构件模型，根据构件实体进行在线修正偏差的机器人自主编程系统。通过分析待加工构件的在线三维重建结果，预先规划加工方案自动生成机器人程序，并通过接触传感器测量加工方案与实际构件之间的偏差，在线修正机器人程序，以消除构件与三维重建模型之间的偏差带来的影响，为机器人编制高效高质量程序提供技术基础。

1 自动编程系统结构

面向大型复杂构件的无模型自动编程系统如图1所示，由工作平台、龙门架及固定在其上的2台激光扫描传感器和2台工业机器人构成。其中工作台用于放置工件，高度300 mm，宽度3 000 mm，长度可根据作业情况延长。龙门架宽4 250 mm，其下端面距工作台1 900 mm。三维传感器中的激光器单点发射脉冲光束并由接收器收到后计算距离，然后通过相控阵或机械旋转装置达到全范围测量。本系统中激光扫描传感器的最高扫描频率为500 Hz，角度分辨率0.25°，距离分辨率1 mm，测量距离为700～3 000 mm，测量角度范围为70°。两台激光扫描传感器分别安装在龙门架的上部两端，可以产生互补的扫描数据。两台焊接机器人倒装在龙门架顶端，通过与可移动龙门架的协同运动使工作空间覆盖整个工作平台。焊接机器人末端的焊枪上安装有接触传感器，该传感器通过焊丝尖端点和构件表面接触瞬间获取接触点的坐标值。它无需在焊枪末端附加任何多余装置，使机器人的可达性不受影响。自动编程系统的计算机通过以太网和机器人控制器相连接。

2 核心算法

系统的核心算法涉及三维重建、自动编程和在线修正等方面。

2.1 三维重建

（1）标定方案。三维重建首先需要对传感器进行标定，文中所用三维传感器直接获取的数据是在一个扇面上按旋转角度采样的距离值。用以扫描器发射光心为原点、扫描面为径面、扫描旋转轴为x轴的柱坐标下的三维向量（ρ，θ，xs）表示，其中ρ为单点采样距离，θ为单点采样角度，xs为采样点x轴分量，由于传感器扫描范围是一个二维扇面，所以该值为常量0。为处理方便，在传感器上建立以传感器发射光心为原点、传感器发射前方为z轴方向，扫描器右方为y轴方向、扫描旋转轴为x轴的直角坐标系。可通过式（1）将所采集的柱坐标系数据转换为直角坐标系下的三维向量（xs，ys，zs）。

xs=ρ·sinθ，ys=ρ·cosθ，zs=0（1）

经过安装后，传感器与基准坐标系构成一个转移矩阵，用齐次矩阵Rsb表示。在本设计系统中，安装传感器时可通过微调传感器使其坐标系与基准坐标系各轴平行，仅在龙门架移动方向即基准坐标系x轴上有偏转。因此传感器坐标系下的数据向量和测量基准坐标系下的数据向量可通过式（2）联系起来。

式中 x0，y0，z0为测量基准坐标系下的扫描传感器的光心原点坐标;γ为扫描传感器发射前方与测量基准坐标系z轴的夹角;xb，yb，zb为测量基准坐标系下表示的测量点坐标。为求解式（2）方程组，需要已知被测点在基准坐标系内的精确数据。由于扫描器发出的激光是一条连续的线，不易确认被测点分别在扫描器坐标系和基准坐标系下的数据。因此，设计了一种立体的特征标定体用于产生标志点。其原理如图2所示。

可通过工业机器人自带的基准坐标查看功能获得标志点A、B、C的基准坐标值。然后从传感器数据中找出因轮廓突变而产生的标志点A、B、C的扫描器坐标值。由于选取的A、B、C标志点具有A与B在z轴上值相同，B与C在y轴上值相同的特点，带入式（2）简化计算扫描器偏转角度，见式（3）

γ=arctan

γ=-arctan

式中 ysA、zsA、ysB、zsB、ysC、zsC分别为A点、B点和C点的对应y轴坐标和z轴坐标。式（3）是因选择多标志点而产生冗余的计算公式，可求其平均值以获得更精确的偏转值。根据已经求得的偏转值代入式（2）可得到其他值。

（2）数据处理及融合。

传感器一次采集的数据经基准坐标系变换矩阵Rsb变换后是m个三维向量（xb，yb，zb）采样点，写成矩阵形式可表示某一时刻工件的一个切面轮廓。设其中一个轮廓为Ci，则有

Ci=xb1，xb2，…，xbj，…，xbm

yb1，yb2，…，ybj，…，ybm

zb1，zb2，…，zbj，…，zbm（4）

這些轮廓依照获取时间的顺序排列可得到一个元素为矩阵的n维向量Q。其中n为轮廓的采集数量，由龙门架移动扫描的速度vscan、距离dscan及扫描器的扫描频率fscan决定，如式（5）所示。

Q=（C1 C2 … Ci … Cn），n=dscan·fscan/vscan（5）

由于n值一般很大，会给数据的处理和存储带来额外负担，因此需要对向量Q进行降维。新向量P的维度与三维重建点云的精度相关。设新向量P的维度是k，则Q可分解成由k个C组成的子向量，对这些子向量进行加权求和得到新向量P的元素Cip，如式（6）所示。

P=（C1p C2p … Cip … Ckp）

Cip=∑（C1+i·（floor（n/k）） C2+i·（floor（n/k）） … Cj+i·（floor（n/k））

… Cfloor（n/k）+i·（floor（n/k）））（6）

式中的P便是一个激光扫描器所生成的点云数据，由于本系统的两个激光传感器均经过标定，所以生成的两个点云数据PR和PL均在基准坐标系下。这就省略了点云配准的步骤和时间，可以进一步提高系统处理速度。

2.2 自动编程

（1）模型表示及焊缝提取。

数字化几何模型一般采用B-Rep 边界法表示。各种复杂的结构均可表示为点和线的信息。因此很适合使用拓扑图来表示构件的几何信息，一个构件的模型可表示为如式（7）所示的无向连通图Gm：

Gm=（Vm，Em）

Vm={v1，v2，…，vm}（7）

Em={e1，e2，…，en}

式中 Vm为图的结点集，对应模型的顶点;Em为图的边集，对应模型的边。焊缝提取就是得到Gm的子集Gw的过程，传统离线编程软件通过人工交互提取焊缝，该方式虽然通用，但在某些特定场合下比较低效。对边ei定义一系列几何相关特征，包括边的长度l、边所在面的夹角θ、边与重力矢量夹角φ、边所在体的厚度t1、边所在体的厚度t2等，如图3所示。

在对应场合下，制定一种按特征向量及其组合量提取的策略。即可通过相关算法自动提取焊缝子图Gw，其中满足关系Gw∈Gm，即焊缝子图Gw是构件图Gw的真子图。

（2）焊接规划。

确定焊接子图后，焊接规划主要在于焊接路径和焊接工艺参数的规划。

a. 焊接路径的规划。

焊接路径的规划即以焊枪末端点工作位姿点，对其移动的先后顺序进行规划，可分为焊缝焊接顺序规划和焊缝间焊枪移动规划。焊缝顺序规划即保证每条焊缝只焊接一次，且根据某种原则确定焊缝的焊接顺序。因为焊缝子图Gw不可能保证是欧拉图，即一条通路能保证经过每条焊缝，所以必须对Gw做因子分解，并保证每个因子都是半欧拉图。即分解结果满足式（8）

Hs={G1，G2，…，Gi，…，Gk}

Gw=G1∪G2，…∪Gi…∪Gk}（8）

式中 Hs为分解结果Gi为分解后的导出子图。

由于导出子图Gi是半欧拉图，所以该图有一条迹是包含该图中所有焊缝且仅包含一次。这条迹可表示为一个有序点集Vgi={vgi1，vgi2，…，vgis}。该有序点集即为机器人在焊接此条焊缝时的工作点序列。然后根据某些原则，如为保证焊接时间最短而考虑每次熄弧点和引弧点距离最短，或者在某些焊接变形较大情况下需要考虑焊缝冷却时间而距离最大的原则，生成一个由有序点集组成的集合。

焊缝间焊枪移动规划即为上一焊缝熄弧后焊枪从焊缝熄弧点无碰撞移动至下条焊缝起弧点的路径规划，文中采用改进的人工势场法，结果是有序点集Vgi和Vgi+1之间插入有序点集Pi={vpi1，vpi2，vpi3，vpi4}。

b. 焊接工艺参数的规划。

焊接工艺参数可以通过人工交互确定，也可以在指定构件材料后，通过焊缝图边集中定义的几何特征集合来匹配焊接参数工艺库确定。

2.3 在线修正

由于三维点云数据点过多，难以直接处理，必须通过提取特征点来简化模型。而模型简化过程中不可避免会引入误差。这使得上述步骤中使用的简化后三维模型与实际生产过程的构件存在误差，包括实际构件尺寸误差、构件定位误差等，会影响自动编程结果的正确性，并严重影响焊接质量。通过进行模型标定可消除构件定位误差。但对于实际构件尺寸误差及构件的变形等问题则需通过在线修正来解决。

机器人通过接触传感器和根据简化模型预先生成的程序在线测量与焊接相关的关键点。其原理是通过对关键点周边一些相关点进行采样，然后根据采样点计算关键点实际位置，并以此为依据在线修正上述步骤中生成的焊接程序关键点。

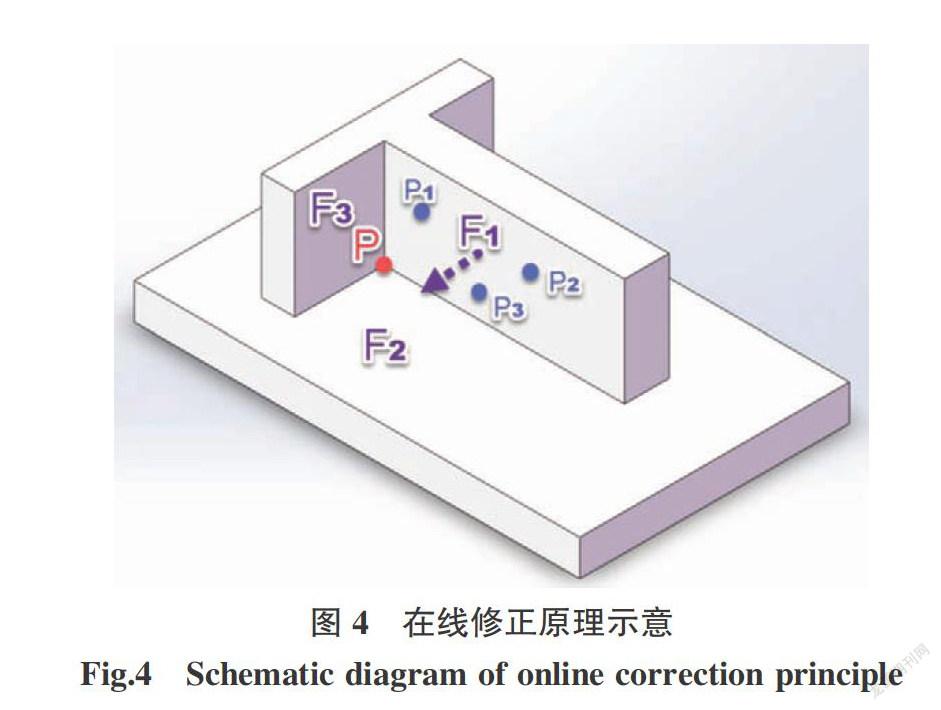
假设某一构件如图4所示，以构件上的一个焊接点P为例，该点由三个面F1，F2，F3相交而成。若已知三个面的法向量及常数项，则有式（9）：

Nx1  Ny1  Nz1

Nx2  Ny2  Nz2

Nx3  Ny3  Nz3xp

yp

zp=D1

D2

D3（9）

式中 xp，yp，zp是交点P的坐标值;矩阵中元素Nx1，Ny1，Nz1为面F1的法向量分量元素，D1为面F1的方程常数项;Nx2，Ny2，Nz2为面F2的法向量分量元素，D2为面F2的方程常数项;Nx3，Ny3，Nz3为面F3的的法向量分量元素，D3为面F3的方程常数项。以面F1为例，为了得到面F1的法向量分量元素Nx1，Ny1，Nz1和方程常数项D1，可以在该面上取三个采样点P1、P2、P3。根据式（10）根据该三点可以确认面F1的法向量分量元素Nx1，Ny1，Nz1和方程常数项D1，式中xi，yi，zi（i=1，2，3）为Pi点的坐标值。

Nx=y1  z1  1

y2  z2  1

y3  z3  1，Ny=x1  z1  1

x2  z2  1

x3  z3  1

Nz=x1  y1  1

x2  y2  1

x3  y3  1，D=x1  y1  z1

x2  y2  z2

x3  y3  z3

面上三个采样点及其采集的起始位置根据数字模型生成，对于特别窄的面，如薄板的厚度面，则根据薄板的侧面位置生成焊枪方向与该面平行的接触点，以保证能采集到采样点。

在线修正即对相应的有序点集Vgi进行在线校准，以Vgi中的点vgij为例，该点以机器人坐标系为基准坐标系，可表示为一个六维向量，向量中前三个元素xj，yj，zj为经过模型标定后基准坐标系下的位置坐标，后三个元素nxj，nyj，nzj为该点的方向向量，该向量是一个单位向量。该点如式（11）所示。

vpij={xj，yj，zj，nxj，nyj，nzj}（11）

3 试验验证

工业构件的复杂性除了体现在机械结构上由多曲面构成外，还有因材质不同造成的不均匀的光学反射率，给三维重建造成了一定的难度。为验证文中系统对复杂性构件的建模效果，选择直径600 mm、高300 mm的卡车轮毂作为构件，轮毂实物如图5a所示，该构件材料为高强钢，具有极不均匀的反光率表面。设置扫描长度为1 000 mm，扫描速度分别为20 mm/s、40 mm/s、60 mm/s、80 mm/s、100 mm/s。扫描后生成的三维点云分别如图5b～5f所示。其点云模型的最大切面直径和对应误差如表1所示，表中点云与图5字母对应。试验表明，随着扫描速度的上升，模型的精度總体呈略有下降的趋势。这是由于在固定的轮廓采集频率下，单位长度内轮廓采集数量下降造成的。但总体而言，在100 m/s以内扫描速度下，模型精度均可控制在3 mm以内。这对于机器人加工前的与设计模型进行定位和匹配是可以满足的。

另外，为验证系统对工件大尺寸和在线速度要求的适应性，对锅炉行业的膜式水冷壁部分构件进行扫描，该构件长3 100 mm、宽400 mm、高6 mm，如图6a所示。设置扫描速度100 mm/s、扫描长度为3 500 mm。扫描后生成的三维点云如图6b所示，点云生成时间为38.3 s（含扫描时间）。实验结果表明：实际上整体系统的三维重建时间由扫描数据采集时间和数据处理两部分组成，其中扫描数据采集时间取决于扫描长度和扫描速度，这与待扫描工件尺寸相关。而数据处理时间基本在3 s左右，工件尺寸对其影响较小。

最后为了验证该系统的自动编程及在线修正效果，对具有曲面和直面的某种型号筋板进行扫描，此结构常见于船舶和钢结构制造业。该筋板长1 000 mm、宽1 000 mm、高120 mm，如图7a所示。图7b是扫描后生成的点云模型，将获得的点云数据进行提取特征点简化并曲面重构得到如图7c所示的三角化模型，该模型为后续加工规划的数据基础。通过人机交互设定好焊缝条件和相应工艺参数后，自动编程系统自动提取焊缝并进行焊接规划，其结果如图7d所示，图中标出了自动提取的焊缝及相应的焊接方向和焊接顺序。然后根据实际构件的位置和自身结构进行在线修正，最终生成作业程序，并下载至机器人控制器运行。

为验证系统所用的修正方法，采用空间位置两点间的欧式距离作为偏差度量。先使用机器人TCP（工具中心点）测量构件的关键点实际位置，即构成焊缝的关键点，如图8所示。获得关键点的位置数据后，计算实际构件与几何模型对应关键点之间的偏差，再计算经过修正后的机器人作业程序中对应关键点与实际构件之间的偏差。两者对比如图9所示，关键点修正后偏差的峰值由20 mm减至4 mm。其中关键点11～16及关键点31～36的修正偏差峰值小于2 mm，且方差也小于其他关键点，这表明当构件关键点处在平面上时，其修正效果好于处于曲面上的。

4 结论

设计了一种能对缺少数字化几何模型的大型复杂构件进行加工规划并可在线修正的焊接机器人自动编程系统。介绍了无模型自动编程系统的构成及工作原理，研究了无模型自动编程系统中所涉及的核心算法，包括激光扫描传感器的标定、轮廓序列的降维和三维点云生成、适合自动编程的构件的计算机表示方法，焊缝的自动提取、焊接任务的规划和对焊接任务的在线修正等。实验结果表明，该系统能够对大型复杂构件进行快速的在线三维重建，并在此基础上进行有效的自动编程，可通过对构件与模型的偏差在线进行，从而保证构件的焊接质量。

参考文献：

[1] 杨志龙，付永领. 弧焊机器人离线编程系统[J]. 航空精密制造技术，2015，51（3）：26-28.

[2] NETO P，MENDES N. Direct off-line robot programmingvia a common CAD package[J]. Robotics and AutonomousSystems，2013，61（8）：896-910.

[3] CHEN Z X，YI J M，LIU J，et al. Off-line programming de-sign of robots based on DXF files[J]. Advanced MaterialsResearc.，2014（1039）：313-319.

[4] CONNOLLY C. Technology and applications of ABB Rob-otStudio[J]. Industrial Robot，2009，36（6）：540-545.

[5] 仲德平，徐洪泽，金晶波，等. 基于RobotStudio的机器人曲面厚板焊接离线编程[J]. 焊接技术，2018，47（1）：45-49.

[6] 邢继生，甘亚辉，戴先中. 基于工件模型的工业机器人自动编程系统[J]. 机器人，2017，39（1）：111-118.

[7] 曹学为. 机械臂自动编程关键技术研究[D]. 北京：中国科学院大学，2015.

[9] WANG C，MENG Z D. An automatic programming methodfor painting robot off-line programming system [A]. Inte-rnational Conference on Mechanic Automation & ControlEngineering[C]. IEEE Computer Society，2012：412-415.

[10] CHEN H P，SHENG W H. Transformative CAD based ind-ustrial robot program generation[J]. Robotics and Computer-Integrated Manufacturing，2011，27（5）：942-948.

[11] 李蒙蒙，孟正大. 基于宏指令的水切割機器人自动编程[J]. 工业控制计算机，2014，27（9）：82-84.

[12] 付泽民，王佳炜，张锁怀. 基于机器视觉的机器人辅助折弯离线自动编程系统的研究[J]. 制造技术与机床，2018（1）：51-56.

[13] 陈珊，周春临. 机器人在多层焊接中的应用[J]. 制造业自动化，2005，27（1）：76-78.