关于“问题链”在几何教学中的应用研究
2020-09-10印春健
印春健



摘 要:近些年来,受到新课程改革的影响,中学数学教学工作的开展更加注重对学生思维方式的训练。尤其对于几何教学内容来说,教师通过利用“问题链”式的教学方法,依靠不同的问题引发学生思考,既训练了学生的思维能力,又提高了几何教学的效率。本文以“问题链”在几何教学中的合理应用对策作为主要的研究内容,从下述几个不同的方面加以展开论述与分析,从而有效提升“问题链”在几何教学中应用的总体水平。
关键词:问题链;几何教学;应用策略
前言:在中学阶段,数学属于主要的学科之一,包含了代数和几何两部分内容,其中,后者的难度更高。几何教学主要利用图形与相关几何语言科学证明图形的性质,较为抽象、难懂,使得很多几何基础较差的学生学习起来非常吃力。特别对于几何课程而言,难度提升,所以,为了改变这种现状,几何教学开展过程中,教师可以运用“问题链”教学方法,帮助学生梳理相关几何知识点,引发学生深入思考,增强对几何知识实际应用的能力。为此,系统思考与分析“问题链”在几何教学中应用的合理对策显得尤为必要,拥有一定的研究意义和实践价值。
一、注重阶梯式“问题链”在几何教学中的科学利用
进行几何教学的过程中,为了发散学生思维,培养其独立思考能力,教师应该注重设计阶梯式的“问题链”,使学生借助不同层级与难度的问题,实现深入思考,全面掌握所学习的几何知识。并且在此过程中,也提高了几何教学的效率。例如:教师讲解人教版几何“旋转”课程内容的过程中,主要围绕旋转作图进行阶梯链问题的合理设计,具体如下:(1)怎样把点A绕点O进行顺时针旋转60°呢?如下图1:
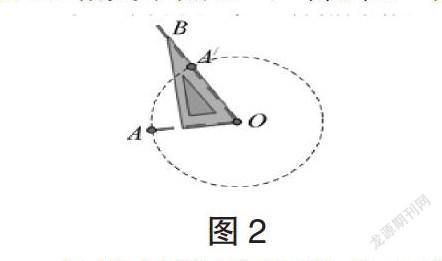
在教师指导下,学生自行探究作法如下,①将AO相连;②沿顺时针作出60°的∠AOB;③将O当成圆心,以OA的长为半径画圆,和OB相交于点A’,得到A’点。见下图2:
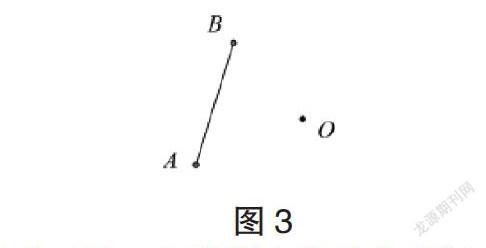
(2) 怎样把线段AB绕点O进行顺时针旋转60°呢?如下图3所示:
此时学生会对上一问题进行归纳与分析,把线段的两个端点A、B依次绕点O沿着顺时针旋转60°,获取相应的A’、B’,连接A’B’得到线段。
(3)怎样把△ABC绕着点O沿着逆时针旋转60°呢?如下图4所示:
学生通过分析前两个问题,把△ABC的三个顶点A、B、C依次绕着点O沿逆时针旋转60°,获得相应的A’、B’、C’,通过连接A’B’C’得到△A’B’C’。
借助上述三个问题的科学设计,遵循由易到难的问题链设计原则,可以帮助学生加深理解相关几何知识,增强几何教学工作的效果。
二、将问题链设计方式合理引入几何概念教学工作中
受到新课程改革的影响,使得中学几何教学工作的宗旨与任务都产生了改变。作为几何教学工作中的重点部分,几何概念教学的开展十分关键。教师通过将“问题链”设计方式合理引入几何概念教学工作中,对加深学生理解相关几何概念与性质十分有益,可以进一步提高中学几何教学工作的效果,完成既定的中学几何教学工作任务。例如:教师讲解人教版几何“中心对称”课程内容的过程中,便运用了问题链设计教学方法,具体如下:(1)以下几张剪纸图案,将其旋转180°之后,与原来图形存在着何種位置关系?然后借助多媒体教学设备为学生呈现相应图片,当学生回答完,再以动画形式加以验证。见下图5:
教师通过引出中心对称图形的内容,并带给学生启发,使其回答出重合的答案。
(2)把线段AB绕其中点O旋转180°,那么,旋转之后图形和其自身存在着怎样的位置关系呢?学生经过思考与分析后,回答:重合。
(3)旋转中心为哪个点?旋转的角度是?学生在思考和分析后,回答旋转中心为中点O,旋转角度为180°。
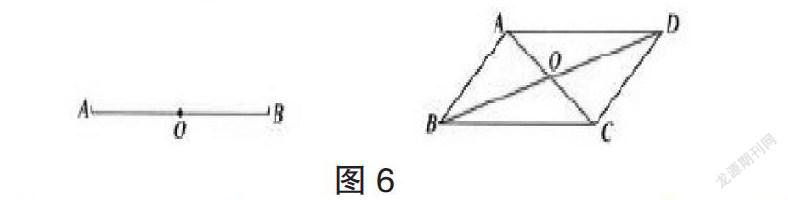
(4)把平行四边形ABCD绕其两条对角线的交点O进行180°旋转之后,会怎样?见下图6:
学生在分析和深入思考后得出答案:重合。教师利用此种问题链教学方法,使学生能够紧密联系之前学过的几何知识,训练了学生的观察能力,加深了对中心对称图形概念的理解。
参考文献
[1]皇玉玲.初中动态几何教学的思考[J].文理导航·教育研究与实践,2018,158(128):1152-1156.
[2]耿莉.“问题链”教学在初中数学教学中的融合[J].新课程导学(八年级中旬),2018,198(156):1646-1650.
