基于波利亚“怎样解题表”的中学数学解题策略
2020-09-10何娇娇
何娇娇
摘要:本文主要基于波利亚“怎样解题表”理论,提出四步解题策略。这一解题策略,加强了解题过程思维的严谨性,数学方法选择的合理性,为解决中学数学综合性题目提供了可行的解题办法。
关键词:中学数学;解题策略;怎样解题
1 理论基础:波利亚的“怎样解题表”
认知过程发生在问题解决当中,为人熟知的波利亚的“怎样解题表”是一种数学解题模式,数学中的解题实际是问题解决在数学这一学科当中的应用。数学学科的特性使得问题解决当中心理活动的占比减少,更多的是一种理性的思考。不少学者对数学问题解决或数学解题方面做了许多研究,也提出了许多理论。其中,波利亚的解题表理论推广更为广泛。他希望借助这个解题表能够使更多的学习者从已有经验出发,通过分析找出普通数学问题的解决通法,同时获得新知掌握新的解题方法。波利亚总结了许多解题模式,其中最引人注目的就是本文所学习借鉴的“怎样解题表”。
2 基于波利亚“怎样解题表”的解题策略
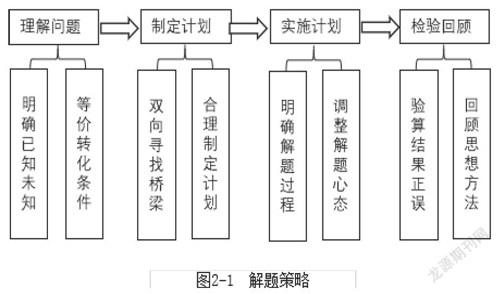
根据对怎样解题表的理解,本文将解题过程分为:明晰已知求解,调动思维联想;双向寻找桥梁,制定合理计划;提升运算能力,调整解题心态;验算结果正误,回顾思想方法。具体见图2-1。
2.1 明晰已知求解,等价转化条件
弄清问题是问题解决的基础。明晰已知求解要求学生在读题过程中保持冷静分析题目中涵盖的信息,问自己几个问题:我能得到哪些条件?这道题目我需要解决什么问题?解决这些问题涉及到哪些知识点?此步骤中,要求学生对圆锥曲线这一块知识框架需要清晰。
明晰所求问题前提下,有目的地将条件等价转化,向求解问题靠近。再次审题,分析题目中是否含有隐藏条件。联想以往有没有遇见类似的题型,若已知的解题方法有与题目有联系的情境,试着用这个方法去分析题目。
2.2 双向寻找桥梁,合理制定计划
找到已知和未知之间的联系,一种是通过联想以往是否遇到过类似的题型或者解题模型,如果有,借助这种方法或模型解决问题。另一种是不能找到直接相关的解题办法,这时候需要双向寻找。在这个过程中,需要思考两个问题:通过已知我们可以得到哪些推论,推论和求解之间有什么样的关系;通过未知求解进行逆向思维,需要什么样的前提才能推出求解;前提和已知或者推论之间是否存在联系,对解题是否有帮助。如果不能解决问题还要进一步思考,需要什么条件才能连接这些信息,是否需要进行多步转化才可以得到我们想要的结果。
对于题目所求有一个清晰的脉络,进而制定合理的计划。利用桥梁,找到解决问题的关键点,制定可行计划。平时的练习过程当中,学生会遇到各式题型,更要注重积累解题的数学思想方法。
2.3 明确解题过程,调整解题心态
实施计划过程中,需要通过制定计划,一步一步将已知条件等价转化为所求问题,在这个过程中,要明确每一步骤是否确实等价,转化的依据是什么。这样才能保证结果的合理性、正确性。若在解题过程中发现不合理之处就需要回到上一步骤,找到问题所在,调整计划。
综合性问题的解题过程运算较为复杂。近些年都以考查椭圆问题为主。其涉及方程的求解、坐标设点运算过程比较复杂,不仅考查学生的知识掌握能力,同时考查学生的运算能力与解题心态。在解题过程中需要有意识地规范书写过程,如果出现错误能够及时检查出来。
2.4 验算结果正误,回顾思想方法
求出问题答案还需再根据解题思路检查一遍解题过程。检验时要注意题目当中是否有限制条件,所得结果是否满足等。所有步骤都完成后,需要回顾本题运用哪些思想方法。在平时的练习过程中注重知识点和思想方法的积累,面对高考题也会更加游刃有余。回顾过程中问自己几个问题:题目涉及了的知识点掌握了吗?题目运用了什么样的数学方法或者蕴含什么样的数学思想?还有别的解法吗?下次遇到类似的题目能快速找到切入点解决吗?
3 總结
解题策略在综合性问题中能够发挥作用的前提在于学生具有良好的基础知识,知晓多种数学方法并会合理运用。解题策略能够帮助学生加强逻辑思维,在解题过程中,帮助学生知晓每一步存在的意义。本文提出的解题策略在难度中等的综合性问题中可以发挥不错的效用,但是遇到难度较大,转化过程比较复杂时,需要学生有良好的心态进行联想转化。有志者事竟成,掌握好的解题策略,在平时不断积累经验,学生的解题能力可以一步一步提升。
参考文献:
[1] 波利亚(G.Polya)著;李心灿,王月爽,李志尧译.数学与猜想:数学中的归纳与类比[M].北京:科学出版社,2001.
[2] 郭昀.数学解题的思维策略研究[J].科技信息,2010(14).
(作者单位:义乌市绣湖小学教育集团春华校区)
