基于车路协同系统的防碰撞预警模型设计

丁俣 孙康 冯吕

摘要：为提高车辆在行驶过程中的安全性，保护驾驶员生命和财产安全，目前智能交通运输系统（ITS）成为了世界各大车企以及汽车研究所的重点研究对象。本文基于其重要子系统：车路协同系统（CVIS），提出了二自由度动态防碰撞模型，并在模型的建立过程中提出了误差补偿半径的概念，其结果表明：相比于传统的单自由度即纵向防碰撞模型，具有更高的安全性和可适应性。

关键词：智能交通运输系统（ITS）;车路协同系统（CVIS）;二自由度动态防碰撞模型;误差补偿半径

0  引言

目前人们对于主动安全系统技术的研究趋于成熟，目前较为普及的安全系统是FCW（前方防碰撞）和AEB（自动紧急制动系统）系统。上述两系统工作原理基本类似，即借助车载雷达或者摄像头采集测控范围内的车辆运动信息，并以此作为输入，经过预警策略模型的分析处理，最终输出预警的结果。但是上述系统由于传感器工作能力和工作条件的局限性，加之无法获取路面环境因素，此时预警策略模型无法体现出对路面环境的适应性，就难免过于理想化。因此对于目前汽车的主动安全系统，引入新的感知技术和预警策略模型十分有必要。

车路协同系统（cooperative vehicle infrastructure system）依靠短程无线通讯技术、自动控制技术、计算机技术实现智能车载单元和智能路测单元间实时、高效和双向的信息交互，并能够以此构建车辆与基础设施的动态网络。相比于传统主动安全技术，此技术具有无感知角度范围限制、不受遮挡物的影响而超视距感知、精准获得邻车状态信息、感知精度不受极端天气影响、可通过路侧单元获取道路环境信息等优势。

本文借助了车路协同系统对车辆信息采集实时性的优点，提出了二自由度动态防碰撞的预警模型。

1  二自由度动态防碰撞的时间模型

1.1 二自由度碰撞点及误差补偿半径

在确定碰撞时间之前，先引入一个概念：二自由度碰撞点。由于传统碰撞单自由度纵向碰撞问题的分析过程中，其碰撞的形式较为单一，即前车车尾与后车车头发生点接触或者面接触，此过程既没有考虑碰撞的方向，也没有考虑碰撞的角度，使得在模型的建立过程中具有极大的局限性。

由于碰撞角度的不唯一性和车身形状的差异性，会导致实际碰撞的位置具有不确定性，以至于难以建立单一的数学模型去涵盖所有的碰撞情况。因此本文采取误差补偿半径的概念，并以此简化二自由度碰撞过程中的数学模型问题。

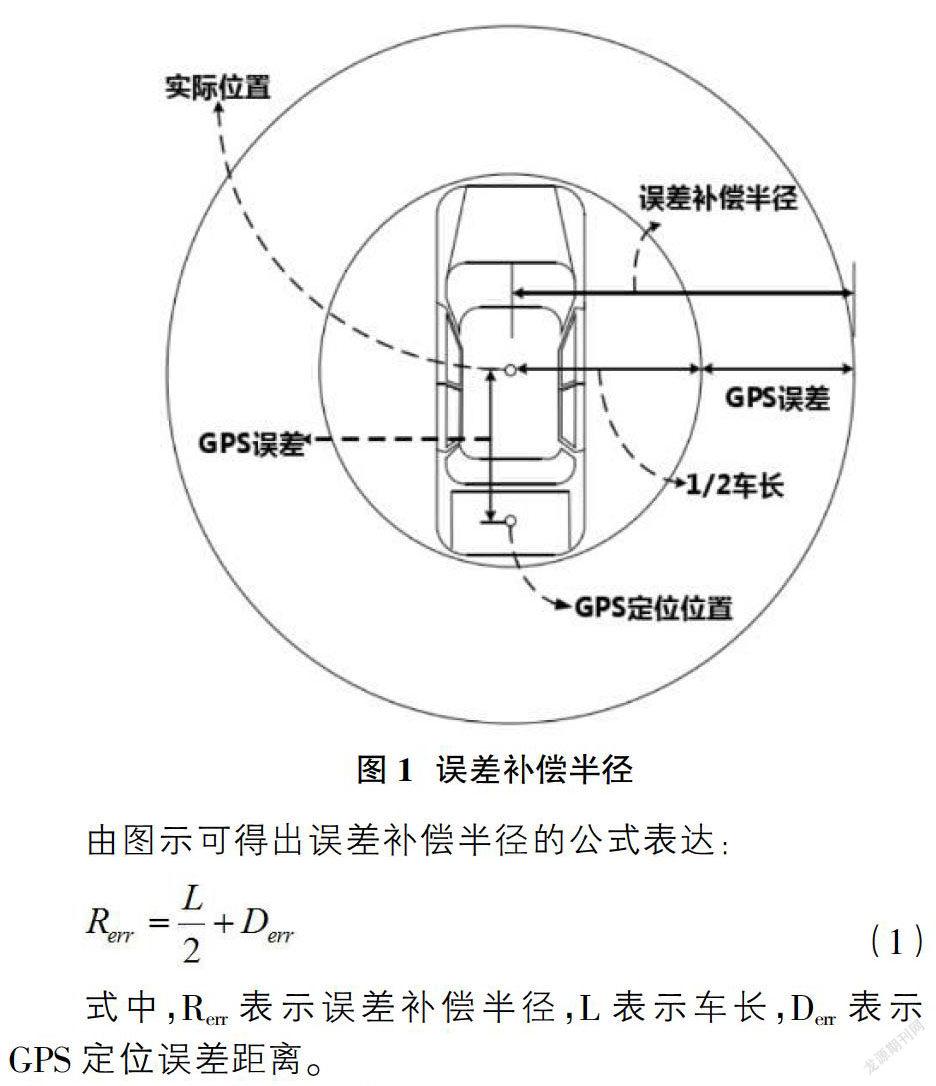
误差补偿半径定义如下：建立一个以车辆自身质心为圆心的刚体圆，将汽车碰撞问题化简为两圆相切或相交问题，但由于车辆尺寸和传感器的感知存在一定的误差会对碰撞点产生影响，圆的半径近似为误差补偿半径。由于本文中车辆的信息由GPS定位装置提供，在分析过程中将误差补偿半径定义为1/2车长加上GPS本身误差。如图1所示。

由图示可得出误差补偿半径的公式表达：

式中，Rerr表示误差补偿半径，L表示车长，Derr表示GPS定位误差距离。

由上式可知，误差补偿半径由车长和GPS定位误差两个参数共同决定，车长可以通过测量获取，但是GPS定位误差距离由于其本身的工作原理比较特殊，且受很多条件因素干扰较大，例如对流层折射和多径热效应等，其误差量无规律可循，要建立一个精确的模型将其定量，十分困难，本文采用现在使用较多的方法——基于高斯分布。

高斯分布是误差原理的基石，是分析众多指标受独立因素干扰的只重要手段。本文仍然使用高斯分布来确定GPS定位误差Derr的分布。假设Derr服从高斯分布，则有高斯分布的概率密度函数：

由于一般情况下GPS不会存在固定偏差，故？滋=0。可以得到如图2所示的概率密度曲线示意图。如图所示，概率密度曲线f（Derr）在区间[-Derr，Derr]中与X轴所构成的阴影部分面积S1含义是：GPS所采集的定位点，落在以本车质心的实际位置点为圆心，GPS定位误差距离Derr为班级的圆里的概率P。且其高斯分布函数的值表示的是：概率密度曲线f（Derr）在区间[-∞，Derr]中与X轴构成的图形面积S2，以上各值得数学关系为：

由上述分析不难看出，对于Derr的求解，需要已知任意一组P与其对应值Derr。

由统计学知识可知，小概率事件一般取概率P=0.05及更小的值，因此本文采用P=0.95時所对应的误差距离Derr即为本文预警模型希望得到的GPS定位误差距离。具体的计算方式需要依据不同的厂商和不同的GPS定位装置所给出的定位精度来进行具体计算得出Derr。

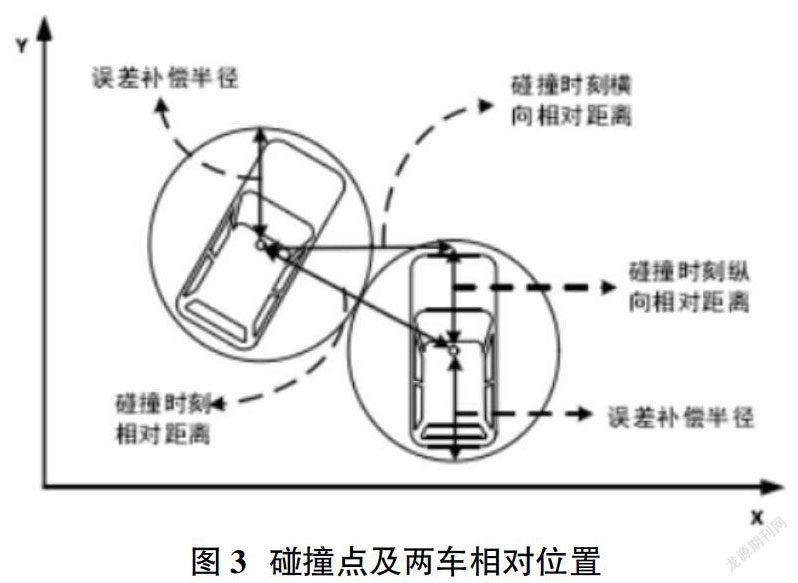
在上文叙述误差补偿半径定义的过程中，提到了将汽车碰撞可近似看作两刚性圆相切的模型，即当以两车质心为圆心，误差补偿半径为为半径的两圆相切时，可判定为两车发生碰撞事故，而此时的切点即为二自由度碰撞点。如示意图3所示，发生碰撞时的两车相对距离L为2倍的误差补偿半径Rerr，在本车坐标系下，将两车的相对距离L按横向X轴和纵向Y轴进行分解，由此可以得到两车横向相对距离Lx和纵向相对距离Ly，且由图显然可以得到：以上三段距离满足勾股定理。

由此可以得到：当两车发生碰撞时，二者的相对位置关系数学表达为：

1.2 碰撞之前两车运动状态的解析

由于车辆是否发生碰撞事故是由车辆碰撞前的运动状态所决定的，所以为了能够动态的预测碰撞发生的时间，本文借助于车路协同系统的优势，即借助DSRC通讯技术、GPS定位技术等，可以动态地获取当前车辆的运动参数。为了能够方便的解析两车碰撞前的运动状态，以下分析过程中采取本车当前时刻作为坐标参考系，即：本车当前时刻的行驶方向始终作为坐标系的Y轴，则与其垂直的方向为X轴，且本车坐标系不会随本车接下来的运动速度或者方向发生改变。然后将本车的运动参数和邻车的运动参数，按照X轴横向分解、Y轴纵向分解，此时二自由度的运动状态可以通过正交分解进行简化。如图4所示，由于在当前时刻本车坐标系里，本车行驶方向始终为Y轴方向，因此本车只存在纵向速度和加速度，邻车运动状态参数vr和ar。设两车的航向夹角为？鬃，则邻车的运动参数可以做如下分解：

完成了运动参数的坐标解析，还需要分析两车在碰撞前有可能发生的运动过程，这个过程有很多种可能性，两车可能是同向而行，也可能是相向而行，而且二者车速也可能是不同的，本文将问题化简，考虑碰撞发生前的某一段特定时间，以两车的相对距离最为参考。可以预测的是：结果一定的时间以后两车的纵向距离可以用如下数学表达：

1.3 动态碰撞时间模型

通过上文的分析过程我们可以得到在碰撞发生前两车纵向与横向的相对距离，本节将引入时间变量t，进一步将距离公式进行解析，得到以时间为因变量的模型，成为动态碰撞时间模型。根据式（7）和（8）其具体推导步骤如下：

由上述模型即可求得未知变量t，进而可以得到二自由度动态碰撞时间TDTTC：

在1.1节论述过程中提到了将两车碰撞化简为两个刚性圆的相切问题，而在本节又计算出了该模型的时间t，当此模型有两个正解值则说明此模型有解，且较小的正值说明两刚性圆相交之前到相切过程中的时间t，较大的正值表示香蕉后再次相切的时间t。因此此模型以较小的正值作为模型的最终解t。DDTTC的物理意义是：二自由度碰撞问题中两车从当前时刻直到碰撞发生的时刻所经历的时间长度。

1.4 二自由度碰撞时间门限模型

上一节根据车辆的运动参数信息，结合碰撞发生的车辆位置关系，求解得到了二自由度动态碰撞的时间TDTTC。结果大量的文献翻阅，在传统的防碰撞预警模型中，有学者提出了可以计算的碰撞时间门限模型：

其中：dbr表示后车减速至与本车同速所经过的制动距离，？驻v表示两车的速度差。

本文采用此模型，并建立一个完整的预警方案设计。

1.5 二自由度动态防碰撞预警策略设计

2  結论

本文突破了传统单自由度纵向防碰撞的理论局限性，借助于车路协同系统对车辆运动参数采集的实时性和高效性，建立了平面范围内二自由度动态防碰撞的预警模型，并采用了高斯分布解决了GPS误差补偿问题，并通过仿真实验证明该模型的有效性和可靠性。

此模型的缺陷在于尚未对防碰撞的时间门限进行分级预警，此策略应在实际使用过程中可能会影响驾驶员的实际驾驶体验，后续的工作将会是根据汽车实际的制动过程以及路面的影响因素进一步指定多级的预警策略来确保更完善的预警系统策略和更好的驾驶体验。

参考文献：

[1]宋晓琳，冯广刚，杨济匡.汽车主动避撞系统的发展现状及趋势[J].汽车工程，2008，30（4）：285-290.

[2]谢建平.基于多车协作感知的主动安全技术研究[D].上海交通大学，2009.

[3]Xuehai  Xiang，  Wenhu  Qin，  Binfu  Xiang.  Research  on  a  DSRC-Based  Rear-End Collision  Warning  Model  [J].  IEEE  Transactions  On  Intelligent  Transportation  Systems，2014，15（3）：1054-1065.