转化思想在小学数学“空间与图形”中的应用

何静

摘要：教育部[1]义务教育数学课程标准（2011）提出把数学教学中的基础知识、基本技能、基本思想和基本经验作为小学数学课程的总体目标。其中转化思想是其他数学思想的基础。而“空间与图形”作为小学数学教材中的四大板块之一，在小学数学内容中占据重要地位，是小学数学教学中的重难点，也是大部分学生最易出错的板块，通过研究如何在“空间与图形”中应用转化思想，让学生把握转化的本质属性，排除非本质属性的干扰在解题中会正确应用转化的思想去解决数学问题。

关键词：小学数学;空间与图形;转化思想

1引言

1.1研究背景

新课程标准指出，新知转化成旧知，复杂难学的问题转化成简单易学问题的都是基于学生认知发展水平对数学教学活动的要求，数学教学目标强调学生在学习中能够理解和运用学习的思想和方法。小学数学教材内容的编写渗透了许多转化为老师在教学中渗透转化思想提供了机会，如果教师认真进行归纳梳理教材内容，会发现小学教材空间和图形模块数学知识总是与前后知识有所联系，存在共性，教学中渗透转化思想帮助学生理解掌握。

2转化思想在空间与图形中的应用

表1人教版小学数学几何图形中体现转化思想的知识点

3.在小学数学“空间与图形”中应用转化转化思想的案例分析

3.1“化繁为简”的案例应用分析。数学家波利亚提出“当原来的问题不可解决时，不要忘记人类的高明之处就在于迂回绕过不能直接克服的障碍，在于能想出某些适当的辅助问题。”复杂的问题通常是由几个简单的问题组合而成，在小学数学图形解题过程中，用作几何图形辅助线的方法，可以清楚直观的将复杂问题转化成简单问题，提高学生的解题速度。

在讲解五年级多边形面积习题时，有一道这样的题：如下图所示，一个平行四边被分成甲、乙两部分，甲的面积比乙大24m2。甲的上底是多少米？

图1例题图示

老师带着学生分析：由图可知，甲图是一个梯形，乙图是一个三角形，要求梯形的上底，我们不仅可以算出梯形的面积根据公式计算上底还可以间接的先求出三角形面积，得到三角形的底，最后求出梯形的上底。提问学生你是怎样计算？你有几种方法进行计算？请列式说说你的计算过程

学生一：20×8-24=136（平方米），136÷8=17（米），20-17=3（米）。

学生的算式似乎并不复杂可经历了较复杂的思考过程：先计算出平行四边形的面积减去甲比乙多的面积24m2，得到由两个相同大小的三角形组成的平行四边形的面积，用它的面积除以高得到三角形的底，最后用平行四边形的底减去三角形的底得到梯形的底。

学生二：20×8-24=136（平方米）136÷2+24=92平方米），92×2÷8-20=3（米）。

这样的解题过程同样复杂，学生通过梯形的面积公式逆向运算求上底。第一步和第一位同学一样得到两个相同三角形的组成的面积，再求出一个三角形的面积加上多出的面积得到梯形的面积，最后根据面积逆运算公式推出梯形的上底。

学生三：（20×8-24）÷2=68（平方米），68×2÷8=17（米），20-17=3（米）。

学生的思维过程同样先计算出一个三角形的面积，然后计算三角形的底，最后求出梯形的上底。这种方法与第一个学生的方法类似，还是首先计算出三角形的底，有所不同之处在于第一种解法是利用组成平行四边形面积求出三角形的底，这里是直接求出三角形面积，然后求底。老师的引导方向也却是如此，想要学生们能熟练的掌握不同的推导过程，并将不同的计算方式进行板书和详细分析，教会学生运用不同的思维进行解题，强调的是让学生掌握多种计算方法和对面积公式的熟练忽略了在多边形面积计算过程中渗透化繁为简的转化思想，大大降低了学生的做题速度和学习效率。下面我将针对本题如何进行化繁为简的转化思想应用进行分析如下：

从上述学生们的的解题思路过程分析可知在该教师的指导下他们对多边形的面积计算及推导过程以及相当熟练了。但是，存在的问题是解题的思维过程十分复杂，这在于做题时会浪费大量的时间降低学生的学习兴趣和学习效率，不利于学生数学思想方法的吸收。然后如果该教师在教学时应用化繁为简的转化思想在图上添加一条辅助线，在甲图中画一个与乙完全相同的三角形画（如下图），问题就迎刃而解。

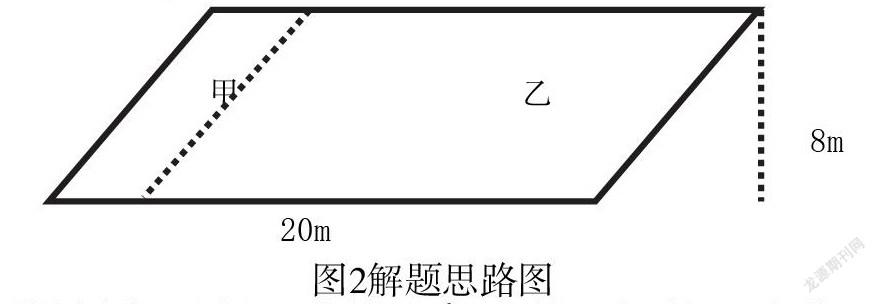
图2解题思路图

从图中知，甲比乙多的24m2正好是一个平行四边形，这个平行四边形的底正好是原梯形的上底，所以梯形的上底是：24÷8=3（米）这样便能快速解决问题，并且能有效提高学生的数学思维。

3.2“化曲为直”的案例应用分析。迈克尔等人将学习分为认知策略、元认知策略和资源管理策略，认知策略则是将新知识通过加工处理找到与已有知识的联系。在小学数学曲线图形学习中就要求学生能够掌握将图形信息进行加工，并且在知识学习的过程中通过模型直观过程中培养学生的观察能力进行有效信息提取加工将新学材料与头脑中已有知识聯系起来达到学习效果。人教版六年级上册教材编排“圆的面积”通过回忆以前用的转化方法把圆的面积转化成熟悉的直线图形的面积来计算。

结语：综合以上转化即保持事物本质不变的情况下改变它的形式，在小学阶段空间与图形板块内容较多，而且并不是所有内容都蕴含着转化思想或者都适合应用转化思想，通过分析研究转化思想在空间与图形中不同表现形式的应用，帮助教师在教学中把握其本质和内在联系，实现教学目的;帮助学生完成在学习过程中的再发现再创造，培养学生的创新意识;帮助学生建立和完善知识体系提高教学效率，从而实现数学化的过程。

参考文献：

[1]中华人民共和国教育部.义务教育数学课程标准[M]（2011年版）.北京：北京师范大学出版社，2011，8～9.