巧用分解思想,妙解复合场问题

◇ 山东 石鸿业

带电体在复合场中的曲线运动综合性强,对思维能力的要求高,许多同学感到无从入手,难以顺利求解.求解此类问题时,若能巧妙地运用运动的分解思想,将复杂的曲线运动化为已知的两个分运动,往往可以快速解决这类问题.下面通过两种不同类型的速度分解,领略分解思想的魅力,希望对提高学生的解题技能、发展创新思维能力有所帮助.

1 一个速度分解为两个速度

D.小球运动过程中可能会出现速度方向与抛出时的方向相反

图1

2 零速度分解为等大反向的两个速度

A.粒子带正电

B.粒子运动到最低点时,粒子所受电场力与洛伦兹力大小相等

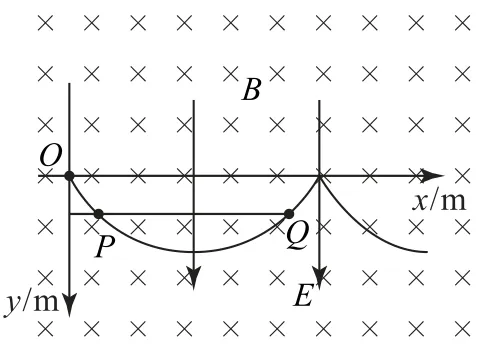
图2

运动的合成与分解是研究复杂运动的重要方法,在解决较为复杂的运动时,常常将其分解为两个比较简单的运动的合成,在应用分解的方法解题时要注意运动的独立性原理,从而提高解题效率.