重复列车荷载作用下季节性冻土区桥墩－基础场地振动特性及长期变形分析*

郑海忠 严武建② 石玉成② 卢育霞② 王 平② 李福秀

（①中国地震局兰州地震研究所，中国地震局（甘肃省）黄土地震工程重点实验室，兰州730000，中国）

（②甘肃省岩土防灾工程技术研究中心，兰州730000，中国）

0 引 言

铁路是国家的基础工程和设施，特别是近年来高速铁路的发展，对国家经济和社会的发展有着重要作用。由于列车运行速度的大幅度提高以及列车运载重量的增加，使得列车振动问题和基础场地动力学问题日益突出，以至于影响列车的正常和安全运行（翟婉明等，2016）。然而在季节性冻土区，由于铁路路基、桥梁、桥墩等在冬季会发生冻胀，而在暖季又会发生收缩，经常受到这种冻融循环的作用，使得在这些地区列车与周围环境的矛盾更加严重。

对列车荷载作用下，铁路路基土体的动力响应和累计沉降的研究主要集中在现场测试、实验分析和数值模拟。在列车荷载作用下，列车及基础场地振动的现场测试研究主要集中在秦—沈铁路、沪宁城际高速铁路、郑西高速铁路以及青藏铁路等沿线，测试结果都表明列车引起的地面振动随距离的增加而衰减，且在距线路一定范围内有一个振动放大区（高广运等，2007；马利衡等，2014；张光明，2014；吴志坚等，2011；董连成等，2018）。夏禾等（2004）对铁路桥梁以及附近地面和建筑物的动力响应进行了现场测试研究，发现地面和建筑物的振动随着列车速度的增加而增加，距离线路越远地面和建筑物的振动越小。陈果元等（2010a，2010b）对铁路沿线桥路和路涵等特殊路线进行了地面振动和沉降实测和分析，得出级配碎石能够有效地减轻地面沉降。对实验分析主要有定点加载、移动加载等实验模型（Yoshitsugu et al.，2005；Liu et al.，2016），此外对地铁也建立了相应的实验模型（关振长等，2017；许晨等，2018；杨文波，2019）。瞿帅等（2017）通过实验研究了长期循环荷载作用下软土的变形特性，并提出了相应的预测模型。数值模型主要有车辆－轨道耦合有限单元模型（翟婉明，2007；翟婉明等，2012）和2.5维有限元模型（边学成等，2008a；Bian et al.，2010）。申权等（2017）利用FLAC3D建立了路堑基础结构模型，分析了道砟和新型排水结构层对列车振动传播的影响。对列车荷载作用下，铁路路基土体累积永久变形的研究主要有：Monismith et al.（1975）提出了指数形式的土体永久变形的经验模型，该模型简单，应用最为广泛。Li et al.（1996）考虑土体的强度参数和在交通荷载作用下土体的动应力分布，提出了路基土体永久沉降模型。边学成等（2008a）利用2.5维有限元模型，计算了列车荷载下土体动力响应，同时，又根据在循环三轴试验土体的变形结果建立了交通荷载作用下土体的永久变形模型（边学成等，2008b）。高广运等（2015）利用半无限空间Mindlin解，同时结合玻尔兹曼线性叠加等原理，提出了列车运行引起的长期沉降模型。

由于我国地形地貌非常复杂，因此铁路沿线不仅有路基还分布着大量的桥梁和隧道。但目前的研究大多都针对铁路路基的动力响应和沉降特性的分析，且这些研究主要集中在饱和软土地区。对铁路桥梁段土体的动力响应和沉降变形研究较少。特别是季节性冻土区，由于长期的冻融循环作用使得铁路沿线场地发生更加严重的沉降和变形，影响路基、桥梁和隧道等的稳定性，进一步影响列车的正常和安全运行。同时，大多数研究都集中在同一基础场地，未考虑不同场地和不同地形地貌对振动传播的影响，然而，不同场地和不同地形地貌的振动效应明显不同。哈大高速铁路是我国目前在最北端季节性冻土区建设的一条标准最高的铁路，铁路全长921 km，运行速度为350 km·h－1。因此，本文选取哈大高铁铁岭—四平段某桥墩及周围不同基础场地为研究对象，进行现场测试，获得了桥墩和基础场地的加速度时程曲线，并分析桥墩和基础场地的振动特性。该桥墩左侧为地面，右侧为高出地面1.8 m的堆积填土，这不仅考虑了不同场地同时也考虑了凸起地形对振动传播的影响。同时，建立对应的有限元模型，将实测桥墩顶端垫石的加速度时程曲线作为动力计算的边界条件，分析桥墩和基础场地在不同季节振动衰减特征和动应力分布情况，并利用土体累积永久变形模型，对季节性冻土区桥墩－基础场地在重复列车荷载作用下的永久变形进行分析。开展季节性冻土区在重复高速列车荷载作用下，桥墩－基础场地的振动衰减和沉降特性，对于我国寒区铁路工程稳定性和安全性预测以及新建铁路工程设计有着重要的科学意义。

1 现场振动测试

1.1 现场测试基本概况

哈大高速铁路位于东北季节性冻土区，土体每年从10月底开始冻结，最大冻结深度能达到2 m左右，土体处于冻结状态的时间可达半年之多，该地区大部分土质属于冻胀敏感性土（艾强，2014）。这为铁路路基、桥墩和基础场地等病害的产生提供了条件，有可能影响列车的正常和安全运行。

如图1所示，在桥墩和基础场地布置了不同的测点，测点1布置在桥墩左侧的基础场地上，测点4布置在桥墩右侧的堆积填土上，测点1距离桥墩0.5 m，测 点4距 离 桥 墩0.1 m，两 者 高 度 相 差1.8 m，测点2和测点3布置在桥墩顶端的支撑垫石上，其测点的布置如图1所示。并于10月份土体未冻结之前，采用中国地震局工程力学研究所研制的891－Ⅱ型测振仪记录不同测点的加速度时程，规定列车运行方向为X方向，垂直列车运行方向为Y方向，竖直向为Z方向。

1.2 现场测试结果分析

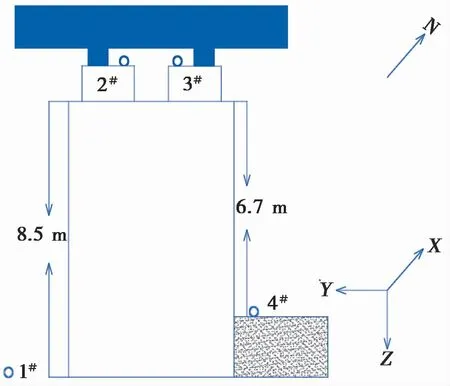
图1 测点布置图Fig.1 Layout of site observation points

铁路沿线场地沉降、变形等主要是由列车运行产生的竖直振动引起的，因此本文主要研究列车经过时，桥墩和基础场地竖向的振动特征。以CRH2C型列车通过时记录到的加速度时程为例，列车的运行速度为262 km·h－1，车厢编组为8节。4个测点的Z方向加速度时程曲线如图2所示。从图中可以看出，各个测点的振动持续时间基本一致，大约为3 s左右；振动加速度单峰值具有明显的周期性（图2c），这是由于每节车厢的轮经过该测试断面所引起的；位于桥墩顶端支撑垫石上的测点2和测点3的加速度时程曲线正负有很好的对称性，正向和负向的加速度峰值基本相等，而位于基础场地的测点1和测点4明显不具有对称性，且正负向加速度峰值相差很大。测点1～4的Z方向的峰值加速度分别 为：33.5 cm·s－2、23.1 cm·s－2、24.5 cm·s－2和64.6 cm·s－2。可以看出桥墩顶端支撑垫石上测点2和测点3的加速度峰值基本相同，峰值加速度相差不大，基础场地的振动加速度峰值明显大于桥墩顶端支撑垫石的振动加速度峰值。显然，基础场地对振动存在着明显的放大作用，同时由于测点4位于堆积填土上，且距离桥墩较近，使得振动放大效应更加明显。

为了进一步分析桥墩和周围不同基础场地振动的振动特性，对4个测点的加速度时程曲线进行能量谱分析（图3）。能量谱分析表明，桥墩和基础场地4个测点的振动能量都集中在30～70 Hz，测点1～3的主频在40 Hz左右，而测点4的主频在70 Hz左右；测点4的能量谱峰值明显小于其他测点，且谱中单峰值的个数多于其他测点，说明其振动能量分布较分散，可以看出基础场地对振动的影响较大。产生这种差异的主要原因是测点4位于填土上，土体较软且振动波会在堆积填土的各个边界上出现折射和反射现象，使得测点4的振动成分向高频移动，且出现多个峰值。

2 桥墩及基础场地动力响应分析

2.1 数值计算模型

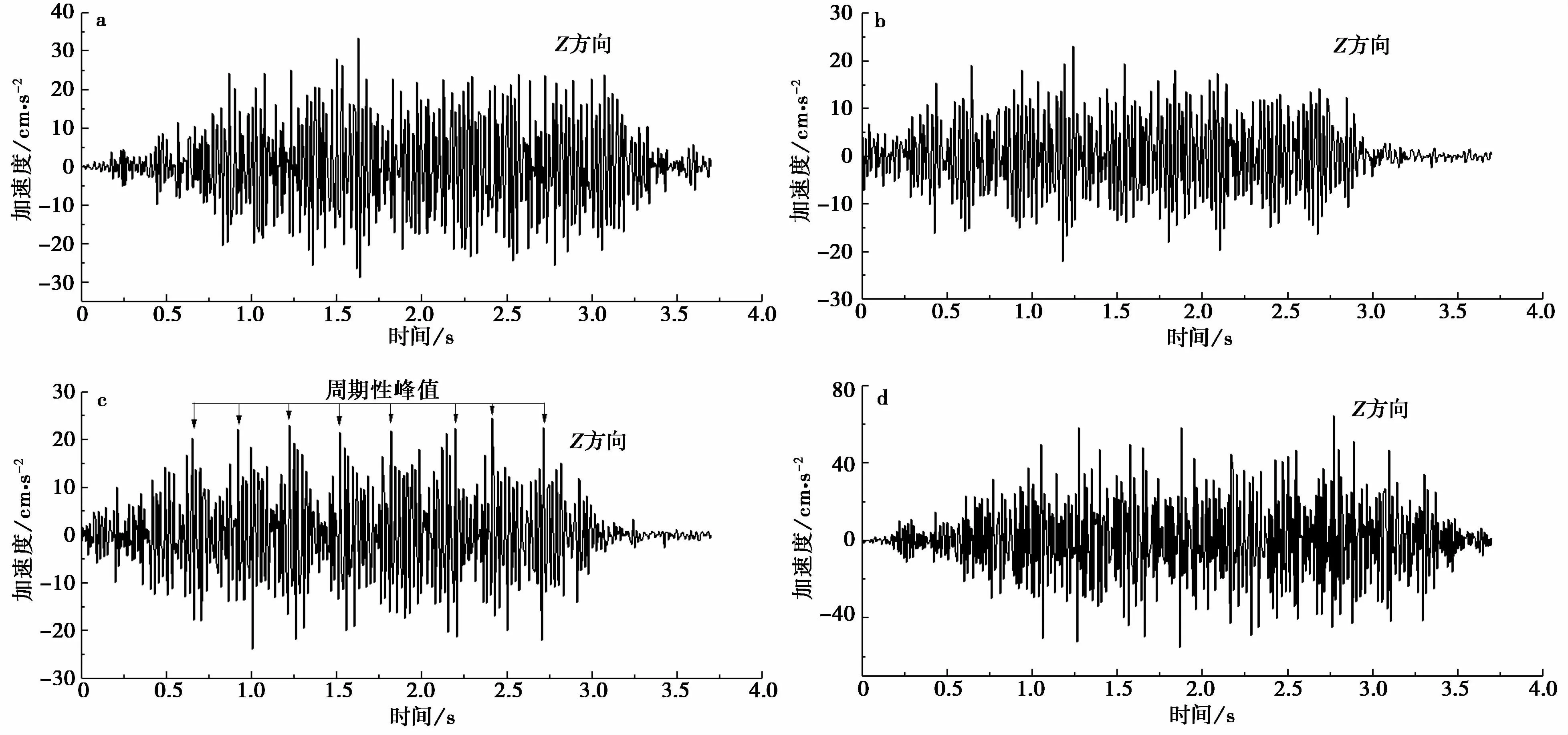
图2 不同测点的Z方向加速度时程曲线Fig.2 Acceleration time history curve of Z-direction at different measuring points

图3 不同测点的能量谱曲线Fig.3 Spectrum curves of different measuring points

为研究在列车荷载作用下季节性冻土区桥墩和基础场地的动力响应和沉降特性，以哈大高速铁路铁岭至四平段某桥墩及基础场地为研究对象，利用ABAQUS建立简化的二维有限元数值计算模型（图4）。模型主要分为两部分，第1部分为土体，土体从下到上依次为9 m厚的黏土，13 m厚的粉质黏土和2 m厚的黄色粉质黏土；第2部分为桥墩，桥墩高为10.5 m，有2 m埋入土体中，截面长度为4 m，采用钻孔灌注桩基础，3根桩，桩长为8 m，截面直径为1 m。桥墩和土体采用平面应变CPE4R单元，为了防止边界对波的反射作用，模型左右两边边界采用无限单元，模型底部完全固定，桥墩顶端将实际测点2的Z方向加速度时程作为加速度边界。在桥墩两侧，土体单元网格划分较密集，尺寸为0.5 m，模型中最大网格尺寸为1×1 m。由于土体划分的有限元网格尺寸与土体的剪切波速和圆频率有关，不允许大于2π·Vs／（14×ω）＝Vs／14f，式中，Vs为土体剪切波速；f为其频率，填土和剪切波速在90～270 m·s－1之间，黏性土在100～450 m·s－1之间（魏鹏勃，2009），f＝1.34 Hz，经计算有限元网格的尺寸不能够大于4.2 m，所以单元网格尺寸1 m满足要求。

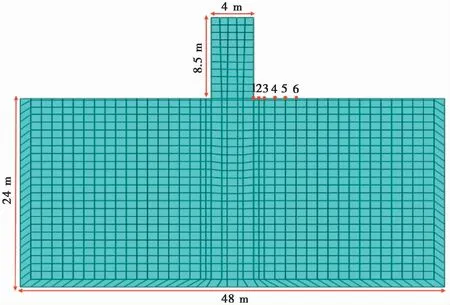
图4 数值计算模型和测点布置Fig.4 Numerical model and layout of site observation points

2.2 数值计算参数

根据哈大高铁地质勘查报告和哈大高铁沿线季节性冻土区的研究可知，哈大高铁沿线的最大冻结深度在93～205 cm之间，不同土层在冻结状态和非冻结时的力学参数如表1所示。在模型计算时，假设土体的材料为理想弹塑性，其破坏准则为莫尔－库仑准则，桥墩和桩基础采用C30混凝土，假设桥墩和桩基础为理想弹性材料，考虑到钢筋的作用，将其力学参数进行适当的提高，取其弹性模型为35 GPa，泊松比为0.2，密度为3000 kg·m－3。

2.3 数值计算结果

为了分析振动的传播特征及不同位置的沉降特性，在数值计算模型的不同位置布置测点（图4），测点1～6与桥墩底端的距离R分别为0im、0.5 m、1 m、2 m、3 m和4 m。同时，在冻结季该测区冻结深度最大为2 m，在数值计算时，假设黄色粉质黏土处于完全冻结状态，其力学参数如表1所示。在模型计算时，首先进行模型自重计算，将得到的自重应力作为初始条件实加在模型上，然后再进行动力计算。

2.3.1 振动传播特征

图5为土体冻结对振动传播的影响。从图中可以看出，在距桥墩0.5 m处，在非冻结季加速度峰值为33.8 cm·s－2，与实际测试的结果一致，说明所建数值模型能够反映出实际情况。

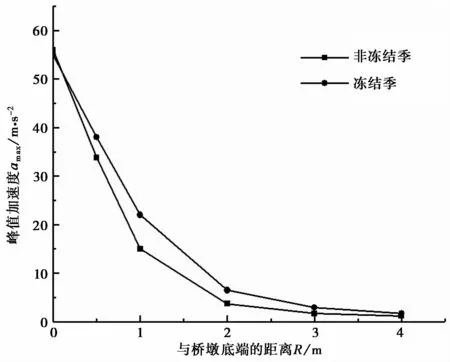
图5 加速度峰值衰减曲线Fig.5 Acceleration peak attenuation curve

无论土体是否冻结，距离桥墩底端越近，桥墩和土体的相互作用越强，加速度峰值越大，振动放大效应越明显，且随着距离的增加，峰值加速度越来越小。在距桥墩底端距离R为0～1 m，峰值加速度衰减速度最快，当R大于2 m时随着距离的增加，衰减速度越来越小。而在冻结季加速度峰值衰减速度明显要小于非冻结季，在相同测点冻结季的加速度峰值要大于非冻结季的，这主要是在冻结季土体弹性模量增大，使得振动波的传播速度快，能量衰减较缓慢，且上部土体处于冻结状态，而下部土体未冻结，形成了明显的分界面，使得振动波在分界面处发生折射和反射现象。

表1 测试区土体的物理力学参数（王超，2014）Table 1 Physical and mechanical parameters of the soil in the test area

2.3.2 基础场地应力分布特性

根据Monismith et al.（1975）和Li et al.（1996）的研究可知，列车荷载作用下引起土体的沉降变形的主要影响因素为动偏应力（qd）。动偏应力qd的计算公式为：

式中：J2为应力第二不变量。

由于本文所建模型为平面应变问题，τzx＝τzy＝0，所以，偏应力qd为：

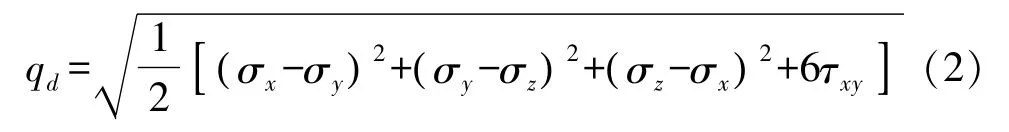
式中：σx，σy，σz，τxy，τzx，τzy为应力分量。

图6为非冻结季和冻结季距桥墩不同位置处动偏应力与深度的关系。从图中可以看出，在非冻结季，距桥墩底端R＝0im的测点1除外，其余测点当深度在0～5 m时，随着深度的增加，动偏应力增加，且在5 m时，达到峰值；当深度大于5 m时，动偏应力随着深度增加而减小。同时，距桥墩越远，动偏应力越小。由于桥墩有2 m埋在土体中，因此桥墩底端R＝0im测点1处土体的动偏应力从深度2 m处开始计算，且当深度为2～4 m，动偏应力随深度的增加而减小，在4～8 m时，动偏应力随深度的增加而增大，与其他测点处的变化规律明显不同。在冻结季，距桥墩底端R为0im、0.5 m和1 m时，当深度为0～2 m时，动偏应力要明显大于非冻结季，当深度大于2 m时，动偏应力受冻结作用的影响较小，与非冻结季的变化规律基本一致，而当深度大于8 m时，各个位置土体的动偏应力在非冻结季和冻结季相等。引起上述现象的主要原因是在距离桥墩较近的位置，由于桩基础的存在，使得其与土体的相互作用加强，土体偏应力增大，而随着远离桥墩土体与桩基础的相互作用减弱，且振动波快速衰减，使得动偏应力越小；在冻结季上部黄色粉质黏土处于完全冻结状态，其弹性模量增大，土体和桩基础相互作用增强，振动波在土层分界面出现反射和折射，使得桥墩附近土体的动偏应力远大于非冻结季；而随着深度的增加，下部土层不会出现冻结现象，因此非冻结季和冻结季的土体偏应力基本相等。可以看出，土体是否处于冻结状态对土体中的动偏应力有着明显的影响。

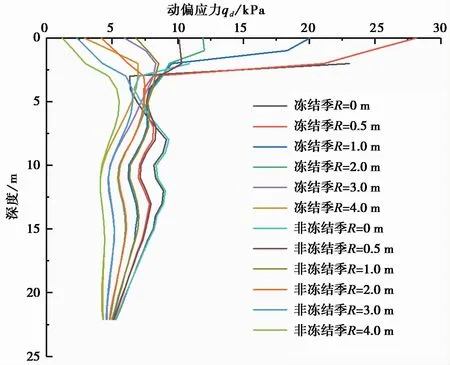
图6 距桥墩底端不同位置处动偏应力随深度的变化Fig.6 Variation of dynamic deviating stress with depth at different locations from the bottom of pier

3 长期变形分析

3.1 列车荷载作用下累计塑性应变的确定

Li et al.（1996）提出基础场地土体在列车荷载作用下的累积塑性应变为：

式中：qd为列车循环荷载下的动偏应力；qf为基础场地土体的静破坏应力；N为循环荷载次数；a、b和m为与土体塑性变形有关的常数。

由于土体的塑性变形参数对累积塑性应变模型的结果影响较大，在应用该模型时，需要选择适当参数。因此，结合吴志坚等（2011）和张峰（2012）的实验结果确定不同土体的塑性变形常数（表2）。

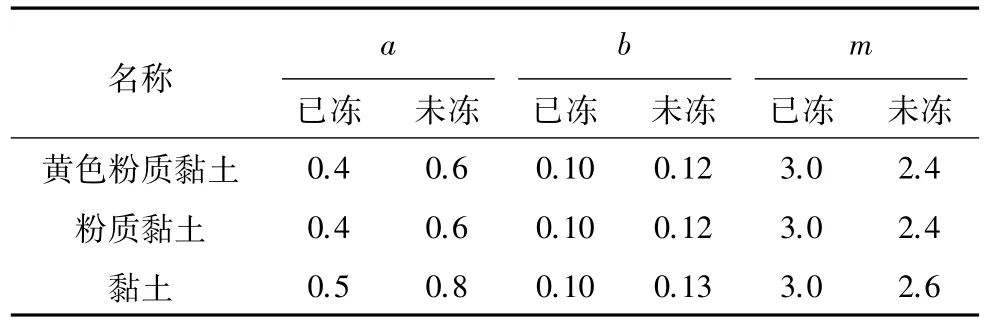
表2 不同土体的塑性变形常数Table 2 Plastic deformation constants of different soils

土体在自重应力下，土体的静破坏力qf为（沈珠江，2000）：

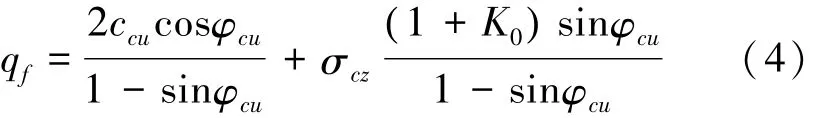
式中：K0为土体的侧限系数；ccu为土体的固结不排水黏聚力；φcu为土体的固结不排水内摩擦角；σcz为土体的自重应力。

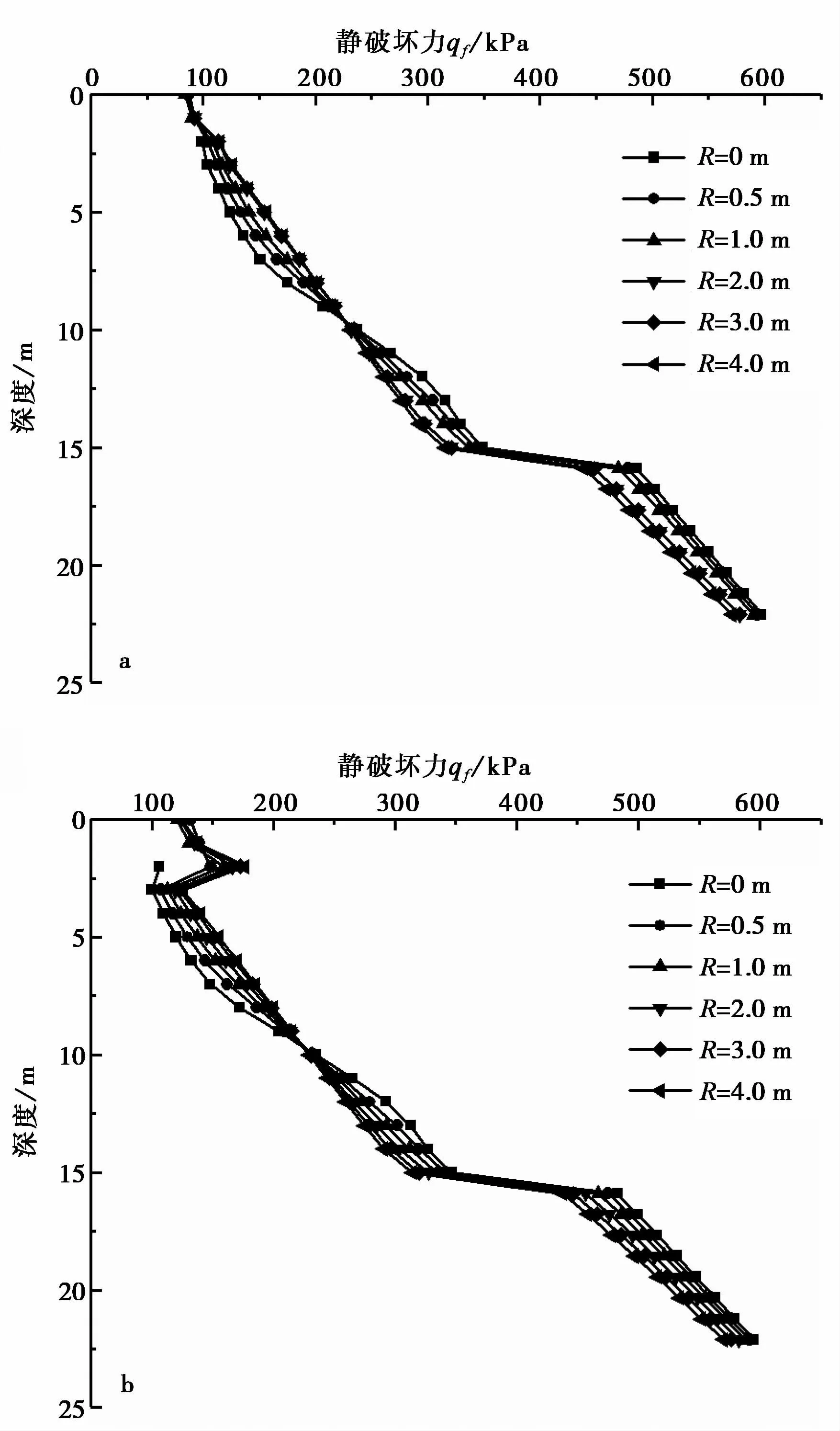
图7 距桥墩底端不同位置处静破坏力随深度的变化Fig.7 The variation of static failure stress with depth at different locations from the bottom of pier

图7为地面不同位置处，土体静破坏力随着深度变化关系。从图中可以看出，不管土体是否处于冻结状态，土体静破坏力总体随着深度的增加而增大；在深度为0～10 m时，桥墩底端R＝0im处的土体静破坏力最小，距离桥墩越远，即R越大，静破坏力越大；深度为10～15 m时，桥墩底端R＝0im处的土体静破坏力最大，距桥墩越远，静破坏力越小；深度为15～17 m时，静破坏力随深度增加的速度明显减小；深度大于17 m时，距离桥墩越近的位置，土体静破坏力越大。但在冻结季，深度为0～2 m时，土体静破坏力随深度而增加，然而在2～3 m时却随土体深度的增加而减小，这主要是因为在桥墩底端R＝0im处存在桩基础，桩自身承担了一部分土体的静破坏力，且桩长10 m，所以深度在0～10 m内其静破坏力最小；随着R的增大，桩基础的作用减小，其静破坏力也随之增大；在冬季，上部的黄色粉黏土处于冻结状态，其黏聚力和内摩擦角都有所增大，而其他土层未冻结，所以静破坏力在深度为2～3 m时呈减小趋势。

根据分层总和法，可以得到重复列车荷载作用下基础场地表面的永久变形Dp：

3.2 桥墩及基础场地沉降计算分析

哈大高速铁路每天运行车次为30，一年列车运行的次数为10i950次，其中有三分之一的运行时间处于土体冻结期，即土体冻结季列车运行次数为3600次。计算得到距桥墩不同测点处基础场地地面累积沉降随列车运行次数的变化。

图8为在不同列车运行次数下，基础场地表面累积沉降在不同测点位置的变化情况。从图中可以看出，在桥墩底端R＝0im处，由于桩基础的作用使得土体累积沉降较小，在距桥墩底端R为0～0.5 m时，桩基础的作用减弱，但土体与桥墩的相互作用较强，使得基础场地累积沉降增加，且在R＝0.5处，沉降达到最大值；当R大于0.5 m时，随着R的增大，土体和桥墩的相互作用减弱，基础场地表面土体累积沉降越来越小，且列车运行次数越多，沉降越大。

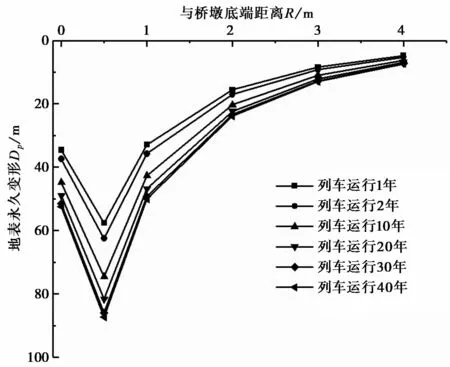
图8 基础场地表面累积沉降随测点位置的变化Fig.8 Change of surface accumulated settlement with location of measuring points in foundation site

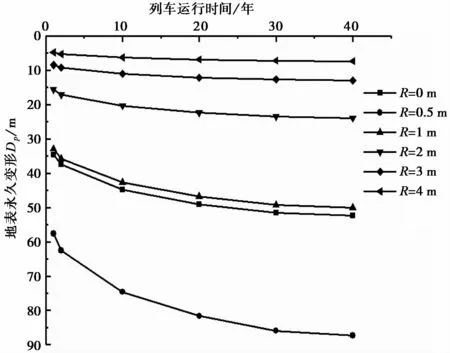
图9 基础场地表面累积沉降随列车运行次数的变化Fig.9 Changes of ground surface settlement with train operation times at foundation site

图9 为在距桥墩底端不同距离处，基础场地地表累积沉降与列车运行次数之间的关系。从图中可以看出，在列车荷载作用最初的2 a时间中，基础场地表面累积沉降速率最大，且除R＝0im外，距桥墩底端的距离R越小，其沉降速率越大。距离桥墩R＝0.5 m处的沉降最大，列车运行1 a后，基础场地表面累积沉降为57.62 mm，运行2 a后，累积沉降增加为62.50 mm，运行10 a后，沉降发展为74.62 mm，运行40 a后，累积沉降为87.32 mm。从图中可以看出，随着列车运行次数的增加，基础场地地表累积沉降增加，且最后趋于稳定。

4 结 论

本文通过选取哈大高速铁路铁岭至四平段某桥墩和基础场地为研究对象，通过现场测试和数值模拟等方法，分析了季节性冻土区在长期列车荷载作用下，桥墩和基础场地的振动特性以及变形特性，主要得到以下结论：

（1）桥墩顶端垫石上的Z方向振动特性与基础场地的振动特性存在着明显的差异，基础场地对振动有明显的放大效应，其加速度峰值要远大于桥墩顶端垫石的加速度峰值，且不同的基础场地的振动特性也存在较明显的差异，堆积填土对振动的放大效应更加明显。

（2）基础场地土体是否冻结对振动传播特性有较大的影响，距离桥墩越远，即R越大，土体和桥墩的相互作用越弱，振动加速度峰值越小，且在冻结季由于土体的刚度提高，振动传播速度加快，振动衰减速度减慢，在相同的测点，冻结季的加速度峰值要大于非冻结季的加速度峰值。

（3）基础场地土体是否冻结对土体中的动偏应力的分布有明显的影响，在桥墩底端R＝0im处，由于桩基础的影响，使得其动偏应力和的分布不同于其他测点，当土体深度为0～5 m时，其他测点的动偏应力随深度增加，而在R＝0im处却相反；当深度大于5 m时，动偏应力随深度增加而减小，且距桥墩底端越远，动偏应力越小，冻结季的动偏应力要大于非冻结季的动偏应力。

（4）基础场地地表的累积沉降在距桥墩底端R＝0.5 m处最大，且随着列车荷载作用次数的增加而增加，最后趋于稳定，当距离桥墩底端R大于0.5 m时，基础场地地表累积沉降随R的增大而减小。