拉－压应力状态下脆性岩石强度及破坏机制颗粒流模拟*

黄 达 李 悦 岑夺丰

（河北工业大学土木与交通学院，天津300401，中国）

0 引 言

深部矿山开采、水电工程地下厂房建设等通常涉及显著的高地应力及强烈的岩体开采扰动。地下工程开挖致使垂直于开挖面方向的应力卸载，扰动区岩体应力重分布。由于岩体内部的非均质性及非弹性，强烈的开挖卸荷会造成岩体某些部位如地质不连续面处发生差异变形（临开挖侧变形快，内侧变形慢），形成卸荷方向的拉应力（Huang et al.，2014；李守定等，2014），与其他方向的压应力组成拉－压应力环境，常诱发开挖扰动区脆性岩体张性松弛、劈裂（表层围岩剥离）甚至岩爆等张性破坏灾害。故拉－压力学行为是需弄清楚的基本岩体力学问题。

然而，以往的岩石力学试验研究多关注于压应力状态试验条件，如单轴／三轴压缩试验、剪切试验等，以及拉伸试验条件，如直接拉伸试验、劈裂试验等。此外，目前开展较多的三轴卸荷试验虽然从加载方式上与实际岩体开挖卸荷相似，但试验过程中岩样内部拉应力无法定量控制。因试验技术上的困难（如胶水粘贴端端部效应以及试样几何及受力对中等），较少开展拉应力参与下的复杂应力状态下的岩石力学试验研究，如拉－压试验、拉－剪试验等（Cen et al.，2017）。目前仅少量学者采用三轴扩张（triaxial extension）试验研究了“狗骨头”形岩石试样在拉－压应力状态下的强度及拉—剪复合断裂特征（Ramsey et al.，2004；Bobich，2005；Rodriguez，2005；Lan et al.，2019）。Cui et al.（2018）和崔振东等（2018）应用扫描电子显微镜（SEM）技术原位观测到了页岩微纳观尺度雁行裂纹，拉－剪复合应力场是其诱因。

数值模拟可以克服试验技术上的不足，为岩石拉－压力学行为研究提供有力手段。颗粒流程序（particle flow code，PFC）（Itasca Consulting Group Inc.，2015）作为一种离散元数值方法在模拟岩石宏微观破裂、损伤演化方面具有显著优势。PFC是以牛顿第二定律与力－位移物理理论为基础，通过简单的颗粒接触黏结机制从细观尺度仿真岩石矿物颗粒及其间的黏结与摩擦，材料的宏观变形和断裂是细观颗粒运动及接触黏结断裂的自然反应。但是，传统的PFC有一个固有缺陷，其模拟的强度在拉－压应力区与真实脆性岩石强度相差较大（图1），单轴压缩强度与单轴拉伸强度之比UCS／UTS（通常仅为3～7左右）相较于真实岩石（一般可达10～20）明显偏小（Ding et al.，2014），无法表现脆性特性。为此，一些学者主要从改变颗粒形状和接触本构等方面提出了一些改进方法（Cho et al.，2007；Ma et al.，2018；蒋明镜，2019）。但这些方法增加了接触模型的复杂程度，产生更多物理参数，对模型参数校核增加麻烦。且现有模拟大多针对压缩试验和拉伸试验研究，很少有开展拉－压复合应力状态下的岩石力学特性，尤其是破坏机制的深入模拟分析。

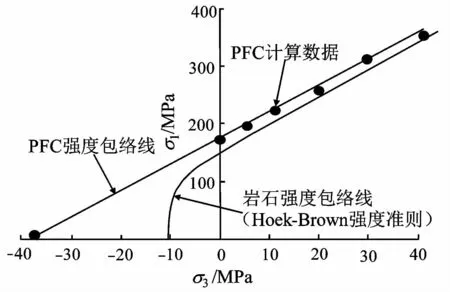
图1 PFC模拟的岩石强度在拉－压应力区与真实脆性岩石强度的差异（改自Diederichs，2000）Fig.1 The difference between rock strength simulated by conventional PFC and real brittle rock strength in tensile-compressive stress zone（modified form Diederichs，2000）

鉴于拉－压应力状态下岩石力学试验的难以有效实施和数值模拟研究的匮乏以及破坏机理的认识不深，本文首先对PFC平行黏结模型（parallel bond model，PBM）的强度准则进行简单改进（采用两个抗拉强度参数），并根据Ramsey et al.（2004）的大理岩拉－压试验结果进行参数校核，可以有效模拟出拉－压应力区的脆性岩石强度特征，得到满意的UCS／UTS，然后进一步深入分析了拉－压应力状态下的岩石宏细观破坏机制。

1 PFC平行黏结强度准则改进

1.1 PFC平行黏结模型

PFC中的平行黏结模型是一种适宜模拟岩石材料的细观颗粒接触本构关系。如图2a所示，平行黏结模型将颗粒间胶结视为一组弹簧（在法、切向分别具有黏结刚度和），与颗粒之间的接触弹簧（在法、切向分别具有接触刚度kn和ks）共同发挥作用。当黏结拉应力（或剪应力）超过黏结法向强度c（或切向强度c）后平行黏结发生断裂，即材料产生微裂纹，大量的微裂纹形成材料宏观裂纹。平行黏结最大法向应力（拉为正）和切向应力计算如下：

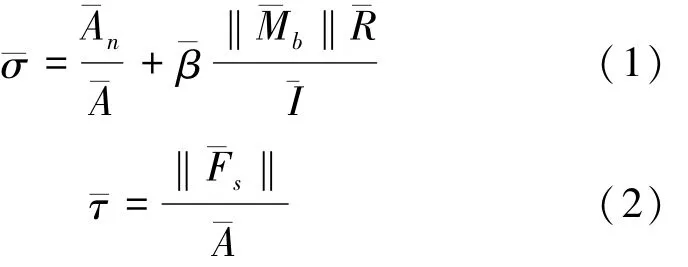
如图2b所示，平行黏结的强度准则采用Mohr-Coulomb准则（在法向抗拉强度c处截断）：

然而，如前文所述，采用该传统平行黏结模型模拟的岩石UCS／UTS明显偏低，因此在模拟岩石拉－压力学行为时有必要进行改进。

1.2 平行黏结强度准则改进

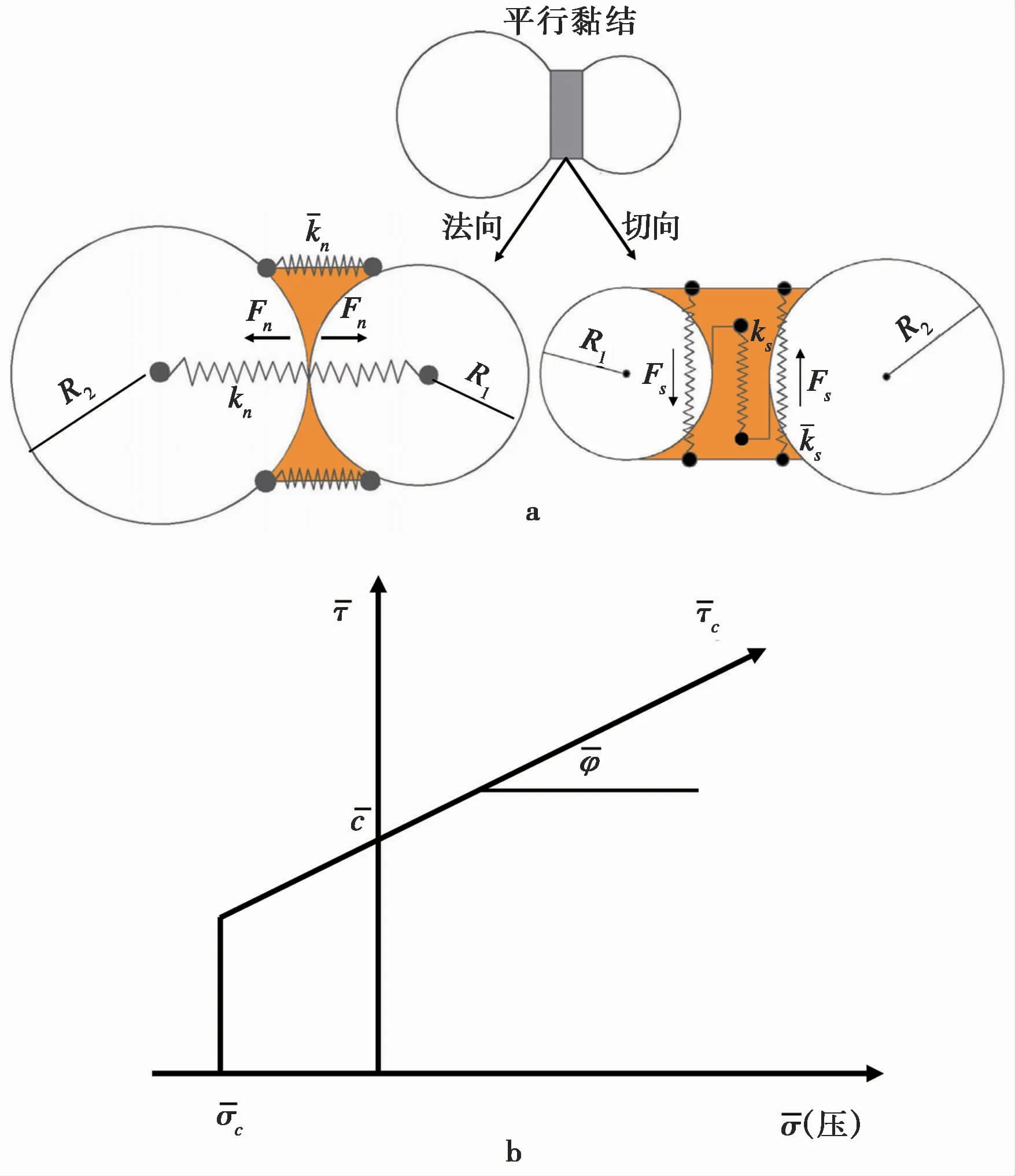
图2 PFC平行黏结模型Fig.2 Parallel bond model in PFC

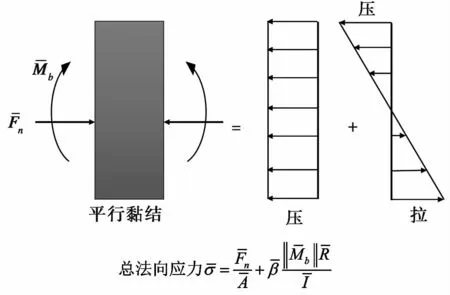
图3 平行黏结法向应力构成Fig.3 Normal stress composition of parallel bond

图4 平行黏结强度准则改进Fig.4 Improved failure criterion of parallel bond

实际上，当模拟的岩石材料主要受到拉应力荷载时，如单轴拉伸，在破裂面处的颗粒黏结受到的法向力多为拉力，岩石拉伸强度主要由较低的黏结抗拉强度c，l决定；而当岩石材料主要受到压应力荷载时，如单轴压缩，破裂面处颗粒黏结有的受到法向压力，有的受到法向拉力，那么对受法向压力的黏结设置相对较高的抗拉强度c，h可有效提高岩石压缩强度，从而可提高岩石的UCS／UTS。下文的模拟结果表明该改进方法是有效的。该方法仅通过改变平行黏结自带的抗拉强度参数，进行简单地编写PFC内嵌Fish语言即可实现，避免了自定义复杂接触模型及其可能引入的新物理参数和拖慢计算速度，具有较强的应用性。

2 脆性岩石强度模拟

2.1 双轴拉－压PFC2D数值试验

采用PFC2D来模拟岩石拉－压试验，模型如图5所示。为了降低计算量以及建模的复杂性，本文采用正方形模型试样。

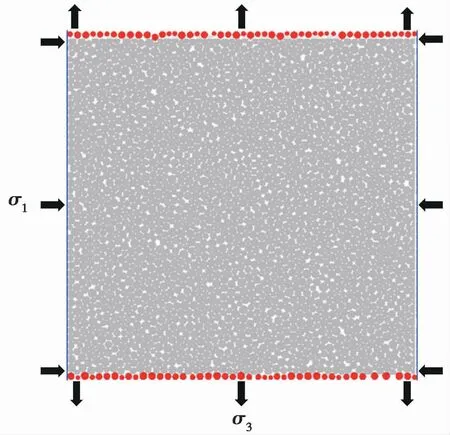
图5 双轴拉－压试验数值模型Fig.5 Numerical model of biaxial tensile-compressive test

首先生成4道墙体围成尺寸为50imm×50imm的正方形模型空间；然后采用粒径膨胀法在该区域内随机生成给定半径的颗粒，并在近无摩擦状态下进行一定时步的循环计算以及浮点颗粒的消除，使颗粒集合体达到均匀密实，然后在颗粒接触处设置平行黏结；最后删除上下墙体并进行一定时步的循环计算以消除内应力。双轴拉－压试验步骤为：先对左右两侧墙体通过伺服加载控制施加预定围压σ1并在试验过程中维持恒定，然后对模型上下边界处的颗粒分别设置向上和向下的同一速率（0.01mm／（106step），属于静态加载）而产生试样轴向拉应力σ3。试样应力和应变通过PFC测量环功能（Itasca Consulting Group Inc.，2015）测得。

2.2 细观参数标定

对某种特定岩石进行模拟时，由于无法试验测得岩石的矿物颗粒间的胶结物理力学参数，PFC模型的细观参数无法直接获取，需要通过校核确定，即不断调试细观参数，直到模拟的宏观力学属性与真实岩石宏观力学属性相一致为止（余华中等，2013；黄丹等，2017）。因此，接触黏结模型在保证有效性的前提下不易太过复杂，否则将增加校核过程的繁琐程度。本文对平行黏结强度准则进行简单改进，即能获得较满意的模拟结果。

由于目前很少有开展较理想的岩石直接拉－压试验研究，本文采用Ramsey et al.（2004）的大理岩拉－压试验（图6）测试的强度（图7）作为模型细观参数校核的依据，校核得到的细观参数如表1所示。该试验的主要原理为围压在试样中心径向方向形成压应力，同时，围压对试样内凹面形成轴向方向的扩张，从而也在试样中心形成轴向拉应力，形成拉－压应力状态。

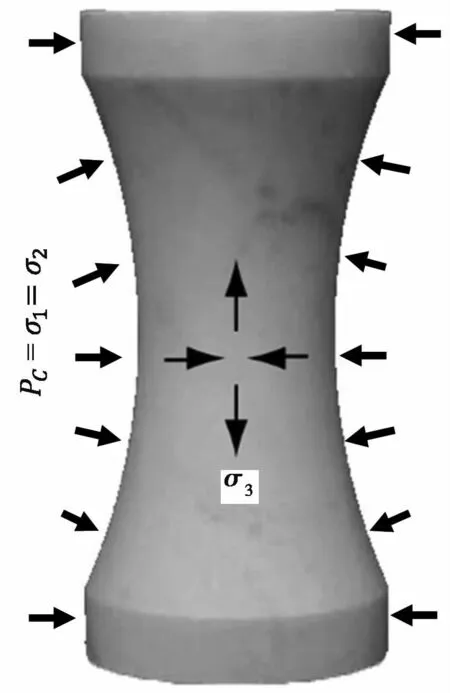
图6 用于细观参数标定的大理岩拉－压试验（Ramsey et al.，2004）Fig.6 Marble tensile-compressive experiment for mesoscopic parameter calibration（Ramsey et al.，2004）

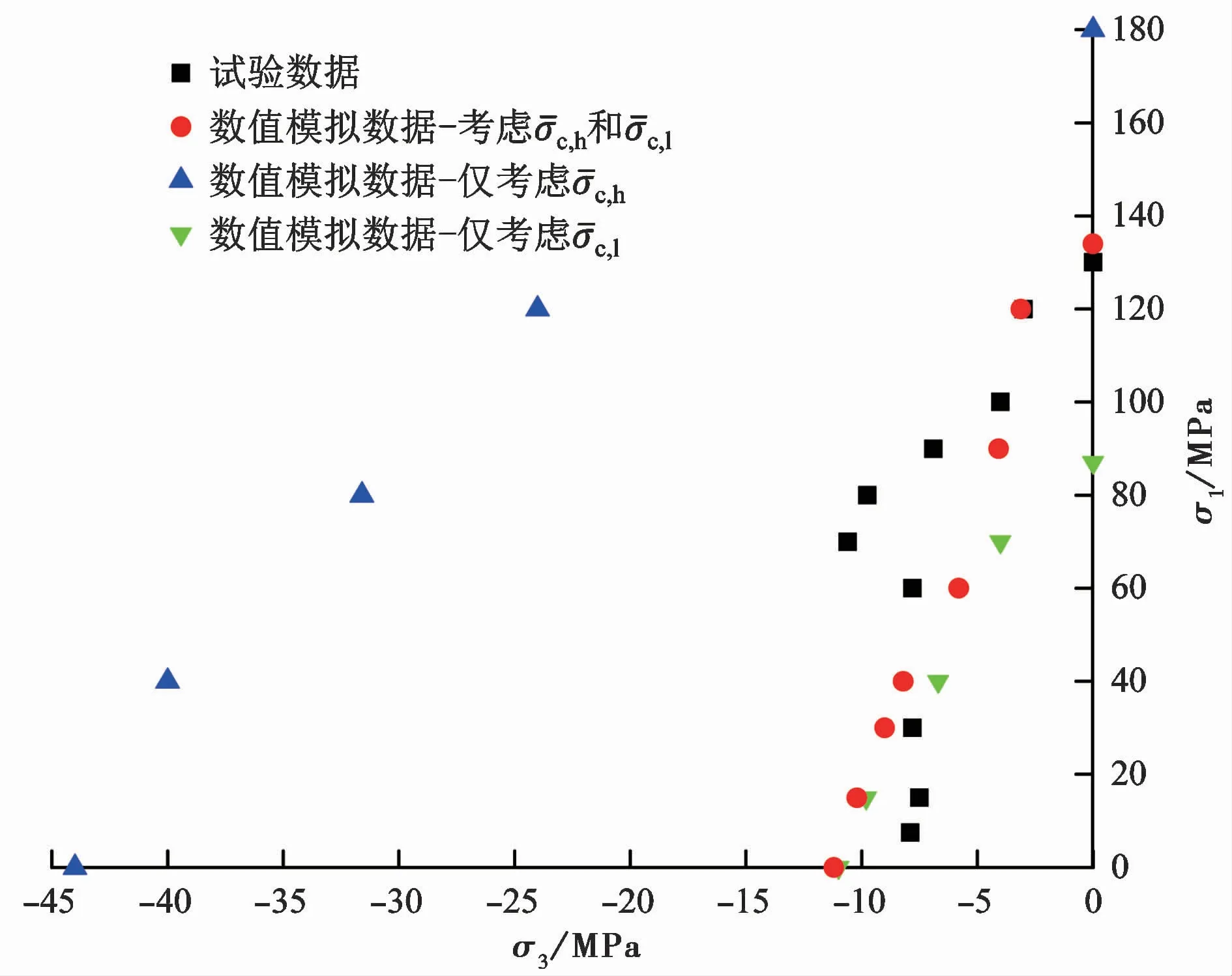
图7 大理岩拉－压强度的PFC模拟效果Fig.7 PFCsimulation effect of marble tensile-compressive strength

2.3 强度的模拟效果

图7为大理岩试验测试的拉－压强度和采用本文改进后的平行黏结强度准则（即采用双抗拉强度c，h和c，l）及未改进的平行黏结强度准则（即采用单一抗拉强度c，h或c，l）的数值模拟结果。总体上，采用改进后的平行黏结强度准则模拟的拉－压强度与大理岩试验结果大体接近，而采用两种未改进的方案模拟的强度与试验结果差距很大。此外，采用未改进的单一抗拉强度c，h或c，l的平行黏结强度准则模拟的UCS／UTS分别为4.1和7.9，与真实岩石相比明显偏低，而采用改进后的平行黏结强度准则模拟的UCS／UTS约为12.1，已能反映岩石的脆性性质。可见本文采用的双抗拉强度平行黏结强度准则可以有效模拟脆性岩石的拉－压强度特征。

3 破坏机制分析

3.1 破裂特征

Ramsey et al.（2004）的大理岩试验得到，在拉－压应力状态下大理岩破裂面力学性质呈拉伸破裂（围压小于65iMPa）和拉－剪混合破裂（围压大于65iMPa）两种类型，拉伸破裂面倾角（破裂面与试样横截面的夹角）基本不受围压影响（其测试数据显示在1°～2°左右），而拉－剪混合破裂面倾角随着围压的增大逐渐增大，典型破裂面如图8所示，当围压为15iMPa、90iMPa、120iMPa时的破裂面倾角分别为1.8°、6.1°以及12.4°。

图8 大理岩拉－压试验典型破裂形态（Ramsey et al.，2004）Fig.8 Typical fracture forms of marble in tensile-compressive tests（Ramsey et al.，2004）a.σ1＝15iMPa；b.σ1＝90iMPa；c.σ1＝120iMPa

图9 为数值模拟的试样破裂形态。总体上，破裂面倾角随着围压的增大而逐渐增大，当围压很小时（如0iMPa、15iMPa），破裂面与拉应力方向基本垂直，为纯拉伸破坏，随着围压水平提高，破裂面倾角逐渐增大，为拉－剪混合破裂。与试验结果稍有不同的是，从很小的围压开始，破裂面倾角便受到围压的影响，这可能与试验的试样形状和加载方式不同有关。数值模拟结果还表明，当围压较小时（如0iMPa、15iMPa、30iMPa）破裂区越集中、破裂面以单条贯通性窄裂纹为主；而当围压较大时（如60iMPa、90iMPa、120iMPa）破裂区较分散、裂纹较宽较断续且呈现雁行分布，其中当围压为120iMPa时有共轭破裂面出现。此外，当围压较小时破裂面总体起伏较小，尤其是单轴拉伸时破裂面整体很平直，其粗糙度为颗粒尺度。

3.2 细观位移机制

裂纹的形成是由于细观颗粒的相对运动而导致颗粒间黏结受力断裂，通过细观颗粒的位移场分析可以进一步解释裂纹形成原因及其力学性质。图10为模拟试样裂纹的细观位移场（每个小箭头表示相应颗粒的位移矢量）。以图10c围压为30iMPa的试样为例，在裂纹两侧绘制总体位移趋势线（粗箭线）D1和D2，并将总体趋势线分解为沿裂纹法向分位移D1n和D2n以及切向分位移D1s和D2s进行分析。图中左侧虚线所圈的裂纹总体上呈水平，其上下侧颗粒位移几乎垂直向上和向下（切向位移分量很小），因此该段裂纹为拉裂纹。同样的，图中右侧虚线所圈的裂纹也为拉裂纹。而图中左侧点划线所圈的裂纹总体上倾斜，其两侧即有法向分位移又有切向分位移且方向相反，因此该段裂纹具有拉－剪性质。同样的，图中右侧点划线所圈的裂纹也具有拉－剪性质。另以图10f围压为120iMPa的试样为例，图中右侧实线所圈的裂纹上、下侧法向分位移为同向且大小差异很小，而上、下侧具有反向的较大切向分位移，故该段裂纹为剪切裂纹。

表1 PFC模型细观参数Table 1 Mesoscopic parameters of PFCmodel

图9 数值模拟的试样破裂形态Fig.9 The fracture forms of the sample in numerical simulationsa.σ1＝0iMPa；b.σ1＝15iMPa；c.σ1＝30iMPa；d.σ1＝60iMPa；e.σ1＝90iMPa；f.σ1＝120iMPa

根据上述分析方法对各试样破裂面处的裂纹力学性质进行判识并以不同线型的圈进行示意。结果可知，在拉－压应力状态下，随着围压的增加，也即随着破裂面倾角的增加，破裂面张性逐渐减弱而剪性增强。这印证了Ramsey et al.（2004）对试验结果的分析：随着围压的增加，破裂面从拉伸破裂（断裂面处晶粒发生穿晶和沿晶界断裂，无摩擦痕迹）到拉－剪混合破裂（具有一定的摩擦痕迹，摩擦区域晶粒粉碎）再到剪切破裂发生转化（全部为摩擦粉碎区，在压－压应力状态下发生）。

3.3 损伤演化特征

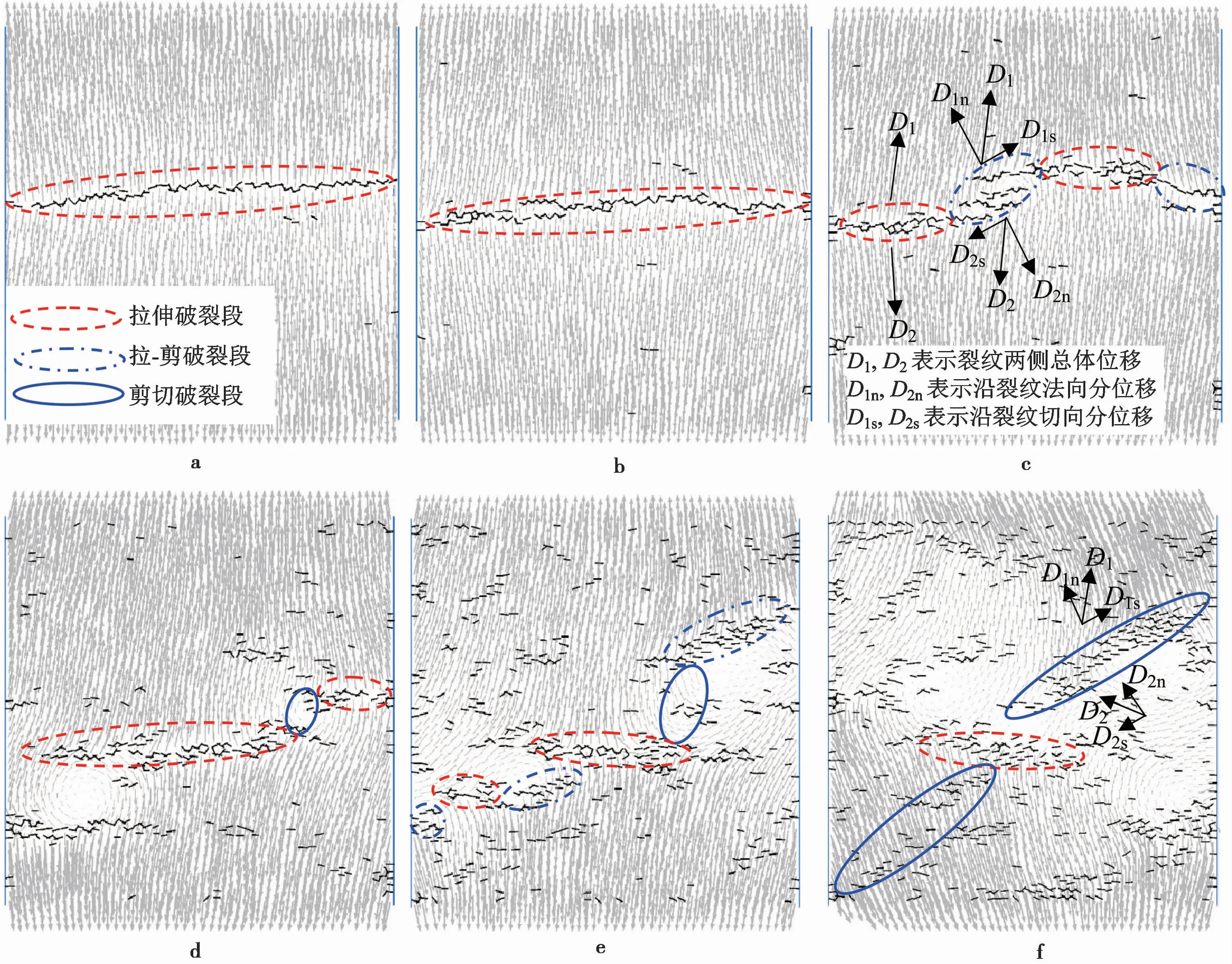
图10 细观位移场及裂纹力学性质Fig.10 Mesoscopic displacement vector field and mechanical properties of cracks a.σ1＝0iMPa；b.σ1＝15iMPa；c.σ1＝30iMPa；d.σ1＝60iMPa；e.σ1＝90iMPa；f.σ1＝120iMPa

岩石的最终破坏是内部损伤累积的结果，PFC模型中的颗粒黏结断裂即代表损伤，产生微裂纹，微裂纹累积形成宏观破裂。故联合应力发展曲线、微裂纹累积曲线、裂纹扩展演化图（图11）以及岩石力学基本常识进行综合分析，探究拉－压应力状态下岩石的损伤演化。如图11所示，以围压为30iMPa和60iMPa的试样为代表进行分析，损伤演化过程大致可分为4个阶段：

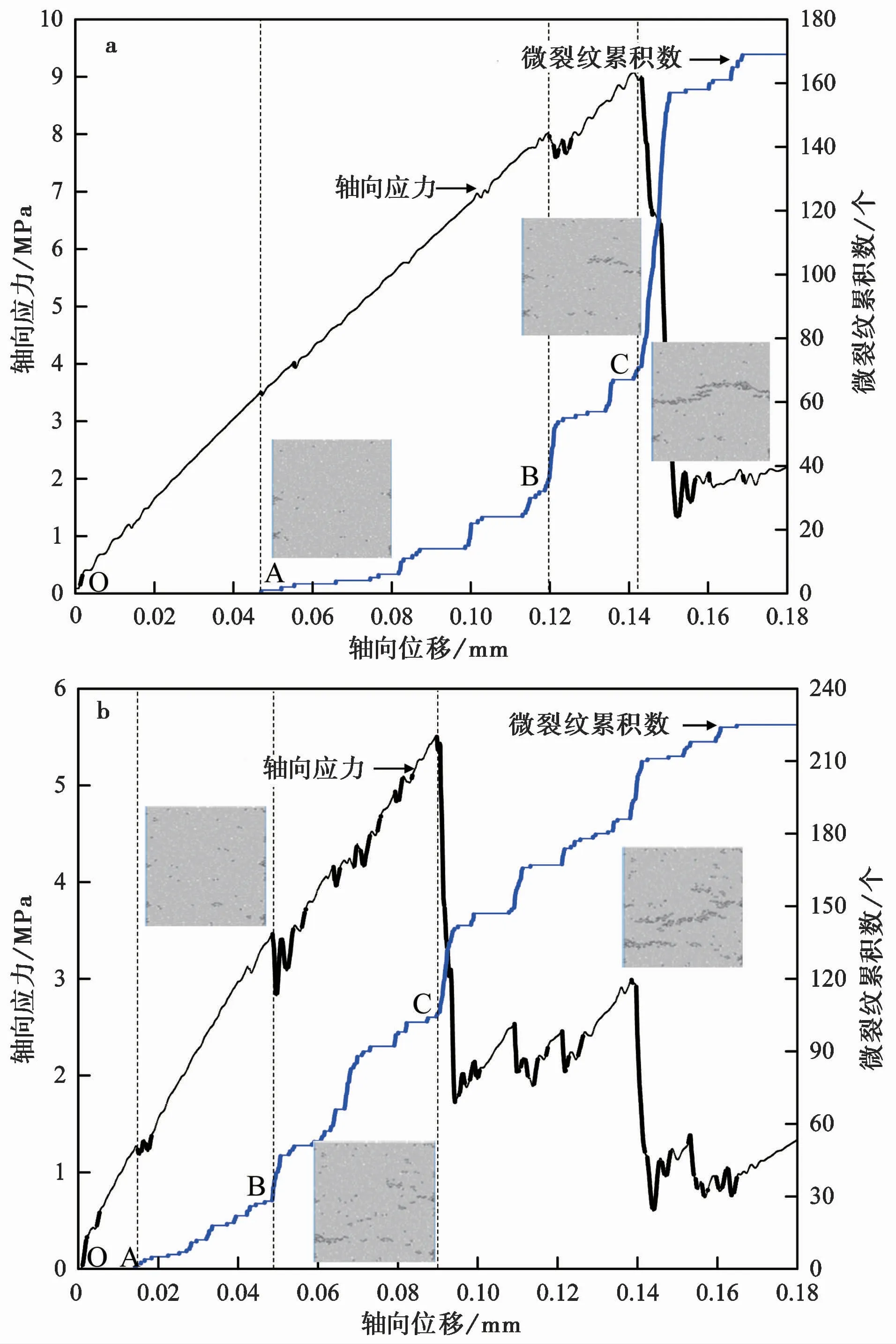
图11 损伤演化过程Fig.11 Damage evolution processa.σ1＝30iMPa；b.σ1＝60iMPa

（1）弹性变形阶段（OA段）：该阶段应力曲线总体呈直线，岩石无损伤发生，微裂纹数为0。围压较大时此阶段相对较短。

（2）稳定破裂发展阶段（AB段）：该阶段随着荷载的增加，应力曲线基本稳定，未出现大的波动。此阶段岩石内部开始出现损伤并逐渐发展，但损伤发展相对缓慢，微裂纹累积曲线呈较小的阶梯状发展，尚无明显宏观拉伸、拉－剪和剪切裂纹出现。此阶段也是围压较大时相对较短。

（3）不稳定破裂发展阶段（BC段）：该阶段随着荷载的增加，应力曲线波动较大。此阶段岩石内部损伤发展迅速，微裂纹累积曲线呈较大的阶梯状发展。此时可见断续的宏观裂纹，但尚未联通成整体断裂面，且两种围压下均以拉伸裂纹为主（其中围压为30iMPa时主要形成在试样右侧，围压为60iMPa时主要形成在试样左下及右侧）。此阶段围压较大时相对较长，且应力曲线波动较大。

（4）整体破裂阶段（C点以后）：该阶段为峰后整体破裂及残余阶段，损伤剧烈发展联通成整体破裂面，应力曲线迅速跌落并进入残余状态，呈现明显的脆性破裂特征。围压为30iMPa时最终破裂面主要为拉伸裂纹和拉－剪裂纹且两者数量相近；而围压为60iMPa时最终主要为拉伸裂纹并伴随少量剪切裂纹。此阶段围压较大时残余阶段更明显，残余段的应力曲线因破裂面摩擦更强而波动较大。

4 结 论

（1）针对传统PFC平行黏结模型不能模拟脆性岩石高单轴压缩与拉伸强度比的问题，对平行黏结模型进行简单改进，建立了双抗拉强度参数的平行黏结强度准则，通过开展拉－压数值试验，得到了与物理试验接近的拉－压强度，实现了岩石高压拉强度比，验证了改进的平行黏结强度准则的有效性。

（2）拉－压数值试验得到了与物理试验结果类似的岩石破裂特征，即随着围压的增加，破裂面倾角逐渐增大，由拉伸破裂转化为拉－剪破裂。数值模拟进一步发现了拉－压应力状态下破裂面处的雁行裂纹，以及根据细观颗粒位移场揭示了破裂面力学性质，发现随着围压的增加（即破裂面倾角逐渐增大），破裂面张性逐渐减弱而剪性增强。

（3）根据拉伸应力曲线、微裂纹累积曲线及裂纹扩展演化图，可将拉－压应力状态下岩石损伤演化过程大致分为弹性变形阶段、稳定破裂发展阶段、不稳定破裂发展阶段和整体破裂阶段（峰后应力跌落及残余阶段）。围压较大时弹性变形和稳定破裂发展阶段相对较短，不稳定破裂发展阶段相对较长较剧烈，峰后残余阶段破裂面摩擦更强、应力波动较大。

另外需要说明的是，Ramsey et al.（2004）开展的三轴扩张试验主要在“狗骨头”试件颈部形成较均匀的拉－压应力状态，破裂也在颈部发生，故本文采用了简化的正方形数值试样模拟颈部区域，拉、压应力加载也更为直接和方便。三轴扩张试验主要用以本文数值模拟的细观参数校核及结果可靠性验证，而本文数值模拟则更进一步从宏微观破裂及损伤演化角度得到了一些有益的结论。