民航客运量与国民受教育水平相关性研究

李忠虎,何 苗

（1.中国民航信息网络股份有限公司 民航旅客服务智能化应用技术重点实验室,北京101318;2.成都民航西南凯亚有限责任公司 研发中心,四川 成都610000）

民用航空运输作为现代运输行业中的重要组成部分,其发展程度代表着国家的经济发展水平,同时民用航空业作为科技型新兴产业,其发展程度还代表着国家科学技术水平.民航客运量是衡量行业发展程度的重要指标,基于OD市场和航线的民航客运量需求预测与分析,对于民航业资源优化配置、交通规划设计和运营管控具有重要意义.［1-4］随着社会进步和国民受教育水平提升,民航市场新增客户中高学历人群占比日益提升,因此研究民航客运量与国民受教育水平的相关性,并借此实现中长期民航客运量预测具有积极意义,特别是中长期的民航客运量预测,将成为民航业交通规划与管理重要的规划基准和决策依据.

1 相关性分析

1.1 数据来源与采集

本文数据来自《中国民用航空局民航行业发展统计公报》、［5］中华人民共和国教育部官方网站发布《教育统计数据-各级各类学历教育学生情况》和国家统计局官方网站,选取2008-2017年的民航旅客运输人次数和各级各类学历教育学生数作为样本数据集,探究民航客运量与国民受教育水平的相关性.

国民受教育水平按照教育部官方网站发布的分类标准,按教育层次类型可以分为:学前教育、义务教育（包括小学和初中）、中等教育（包括高中及中等职业教育）、高等教育（包括研究生、普通本专科、成人本专科、网络本专科和高等教育自学考试本专科）和特殊教育五种类型;按照教育阶段类型可以分为:招生、在校、毕业三个维度.

1.2 指标相关性度量

皮尔逊相关系数用于度量两个连续变量之间的相关性,其值介于-1 与1 之间,两个变量 iX和 jX 总体间的皮尔逊相关系数 ji,XXρ 定义为:

其中Xi表示第i 指标变量, cov(Xi,Xj)表示第i 指标变量和第j 指标变量之间的协方差,δXi表示第i 指标变量的总体标准差,μXi表示第i指标变量的总体均值.

两个变量间的皮尔逊相关系数无法直接求出,必须先收集两个指标变量对应的样本,求出两个变量样本间的皮尔逊相关系数,进而估算两个变量总体间的相关系数.两个变量Xi和Xj样本间的皮尔逊相关系数 rXi,Xj定义为:

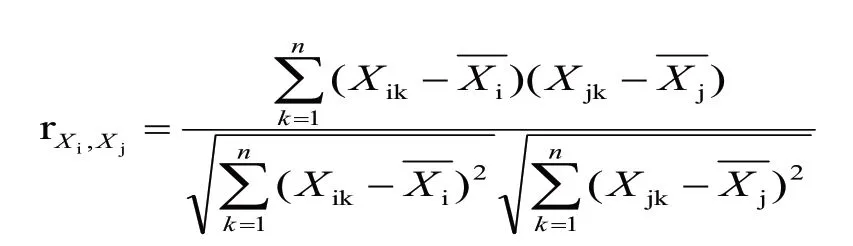
其中ikX表示第i 指标变量的第k 个分量,n为样本量.

1.3 相关性分析

本文相关性分析均选取2008-2017 年数据样本,民航客运量通过客运人次数来刻画,各教育类型就读规模为对应教育类型招生、在校和毕业的总人数.首先分析近年民航客运人次数及各教育类型就读规模的相关性,在0.01 水平上与民航客运人次数显著相关的变量为:高等教育就读规模、学前教育就读规模和义务教育就读规模.

表1 民航客运量与各教育类型就读规模的相关性

民航客运量与高等教育就读规模的皮尔逊相关系数高达0.971,进一步分析民航客运量分别与高等教育招生规模、在校规模和毕业规模的相关性.在0.01 水平上这三个变量均与民航客运人次数显著相关,民航客运量与高等教育毕业规模相关系数最高,皮尔逊相关系数值为0.984.

表2 民航客运量与高等教育各阶段规模的相关性

1.4 构造强相关字段:40 年滚动累计普通本专科毕业规模

经过前面的相关性分析,我们得到了与民航客运量显著相关的变量:高等教育毕业规模,皮尔逊相关系数为0.984,接下来通过调整数据计算口径、提出适当假设等方法,在高等教育毕业规模的基础上构造相关系数更高的字段.

1.4.1 年度滚动累计口径

聚焦高等教育毕业规模数据字段计算口径,各年高等教育（包括研究生、普通本专科、成人本专科、网络本专科和高等教育自学考试本专科）的毕业总人数,但是仅用一年的毕业人数无法有效刻画国民受高等教育的整体规模,故引入年度滚动累计口径,构造字段40年滚动累计毕业规模.

40 年滚动累计普通本专科毕业规模,表示从当年开始（包含当年）向前追溯共计40 年每年普通本专科毕业总人数累加和,即X 年40年滚动累计普通本专科毕业规模,即为（X-39）年至X 年（包含（X-39）年和X 年）各年普通本专科毕业总人数,即为（X-35）年至（X-4）年（包含（X-35）年和（X-4）年）各年普通本专科招生总人数.

1.4.2 提出数据假设

用当年高等教育毕业人数预测当年民航客运量,时间上存在明显滞后性,故根据大致实际情况,提出适当假设:普通本专科招生数即为4 年后普通本专科毕业数.

鉴于该数据假设,获取国家统计局官网1949-2018 年普通本专科招生数,采用年度滚动累计口径,构造字段40年滚动累计普通本专科毕业规模,并分析民航客运量与该字段的相关性,皮尔逊相关系数为0.994.

表3 民航客运量与40年滚动累计普通本专科毕业规模的相关性

2 民航客运量预测模型

根据前面的相关性分析,民航客运量与40年滚动累计普通本专科毕业规模呈现强正相关,并且基于假设未来4年的毕业规模可由前期招生规模推算,即2019 年至2022 年40 年滚动累计普通本专科毕业规模,分别为1976-2015 年普通本专科招生总人数、1977-2016 年普通本专科招生总人数、1978-2017 年普通本专科招生总人数、1979-2018 年普通本专科招生总人数.接下来将采用单变元回归的方式建立模型,并预测未来两年的民航客运量.

民航客运量与40 年滚动累计普通本专科毕业规模,近年明细数据详见表4 .

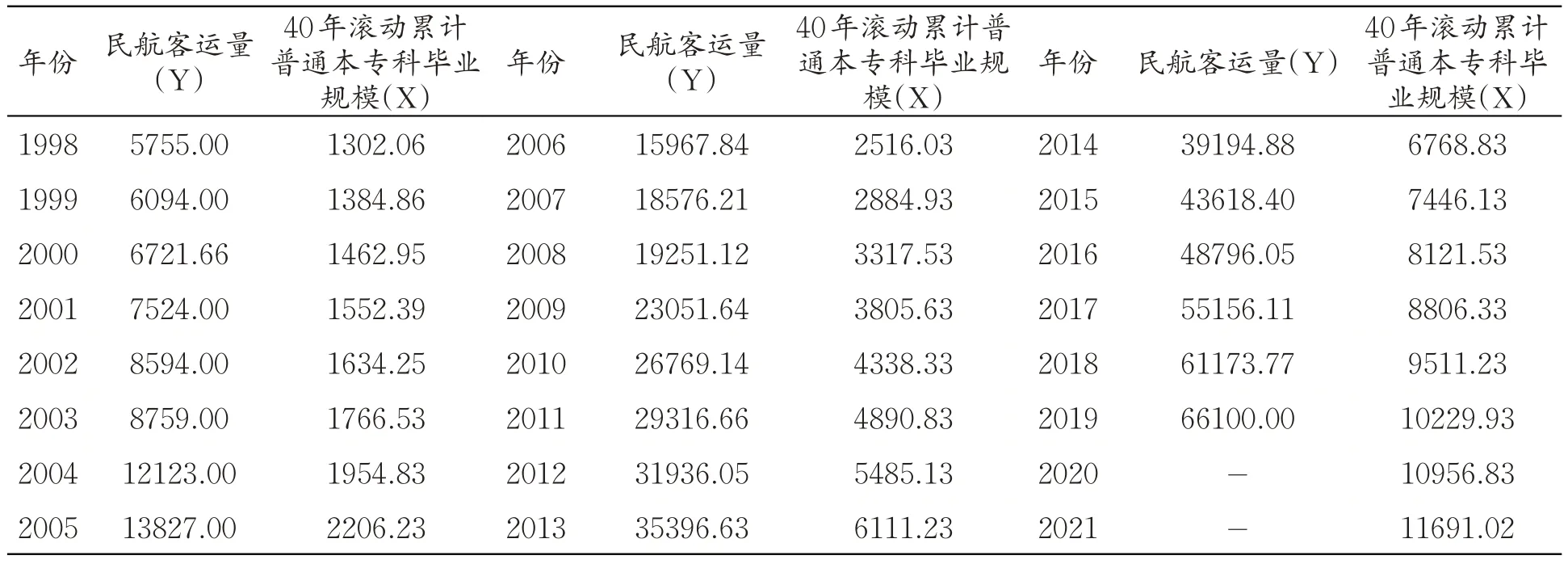
表4 民航客运量（Y）与40年滚动累计普通本专科毕业规模（X）数据（单位:万人）

2.1 建立回归模型

根据表4 中1998-2019 年明细数据,我们将尝试采用普通最小二乘（OLS）回归法,［6-7］包括简单线性回归、多项式回归拟合模型,并评价拟合优度、检验假设条件和模型的选择.

普通最小二乘（OLS）回归拟合模型的形式:

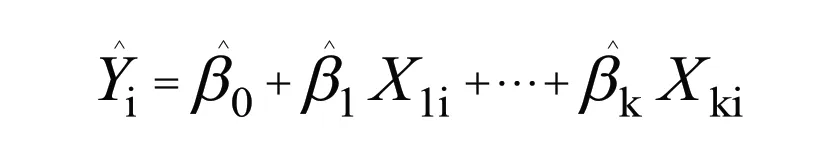
其中,i=1……n,n为观测的数目,k为预测变量的数目,为第i 次观测对应的因变量的预测值,Xji为第i 次观测对应的第j 个预测变量值,为截距项,为预测变量j 的回归系数.我们的目标通过减少因变量的真实值与预测值的差值来获得模型参数,即残差平方和最小.

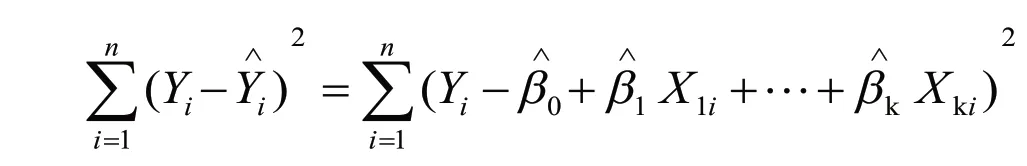
为了能够恰当解释OLS 模型的参数,数据必须满足以下统计假设:正态性:对于固定非自变量值,因变量值成正态分布;独立性:Yi 值之间相互独立;线性:因变量与自变量之间为线性相关;同方差性:因变量的方差不随自变量的水平不同而变化.

当回归模型包含一个因变量时,我们称为简单线性回归.当只有一个预测变量,但同时包含变量的幂（比如,X、X2、X3）时,我们称为多项式回归.

利用数据分析软件建立由40 年滚动累计普通本专科毕业规模（X）预测民航客运量（Y）的OLS简单线性回归,利用软件分析D.W统计量为0.461,残差独立性未通过检验,并明显存在尾部预测数据值过低的问题,详见图1.

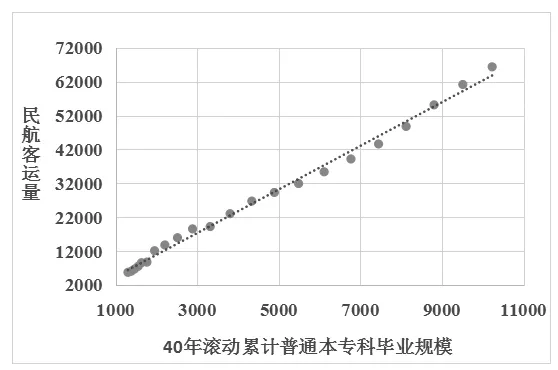
图1 普通最小二乘（OLS）简单线性回归

建立由40 年滚动累计普通本专科毕业规模（X）预测民航客运量（Y）的二次多项式回归,D.W 统计量为0.487,残差独立性仍未通过检验.进一步建立三次多项式回归,由于次数偏高,出现拟合曲线变化趋势过快,预测值显著偏高的突出问题.

为降低多项式回归次数,尝试引入变量lnX建立回归模型,通过软件分析详细的输出见表5.

表5 变量初始分析

接下来进行回归方程与回归系数的显著性检验.

显著性检验的原假设H0:回归系数与0 无显著差异,检测采用F 统计量和t 统计量,该回归模型F统计量为5505.780,对应概率值0.000小于显著性水平0.05,则拒绝原假设,表明回归系数与0有显著差异,即因变量与自变量有线性关系,回归方程有意义.由表5中最后一列回归系数,对应概率值小于显著性水平0.005,表明回归系数显著不为0,即在控制其他变量不变时,变量X2、X、lnX均分别与Y线性相关.

模型的R2 值为0.999,表明模型的方差解释率为99.9%,初步判断模型拟合效果很好,模型的表达式为:Y=0.001X2-4.600X+20598.601lnX-137739.041.

最后进行残差分析,［8］正态性:从标准化残差直方图、标准化残差的P-P 图来看,散点近似均靠近斜线,近似满足正态性,详见图2、图3;独立性:模型的D.W 统计量为1.849,接近2.0 落在无自相关性的值域中,认定残差独立通过检验;同方差性:残差散点图拟合的直线大致平行于横坐标,可以大致认为残差是齐性的.经过残差分析,该回归模型有效且拟合效果很好.

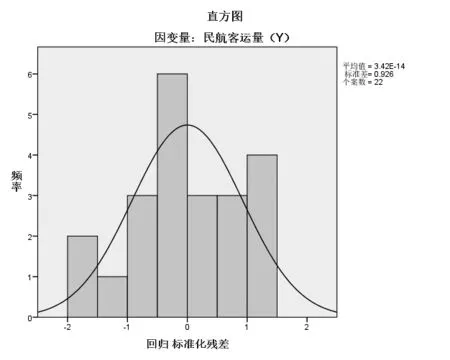
图2 标准化残差直方图

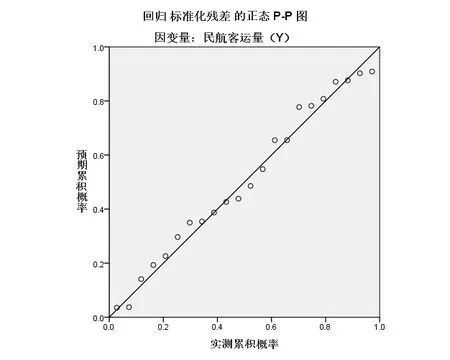
图3 标准化残差直方图和P-P图

2.2 模型预测

通过残差检验,前面建立的回归模型有效,于是可得到未来两年年民航客运量（Y）的预测值详见表6,旅客量的年增长率在10%-11%之间,符合民航客运量整体增长趋势.

表6 2019-2022年民航客运量预测值（单位:万人）

结 论

在许多关于民用航空客运量影响因素的实证研究［9］中,多用国内生产总值、人均国内生产总值及铁路客运量作为因变量来建立回归模型进行分析和预测,本文从国民受教育水平出发,发现高等教育毕业规模与民用航空客运量有着显著的相关性.进一步构建强相关变量40年滚动累计普通本专科毕业规模,并建立回归模型实现对民航客运量的未来两年的预测,预测值契合民航客运量增长的整体趋势.