信息匮乏背景下基于Voronoi的无水港选址模型——以几内亚湾为例

张恬，李悦超，郑长江，杨海飞

（1.中国港湾西部非洲区域公司，Abidjan 科特迪瓦 06 BP 6687；2.河海大学，江苏 南京 210098）

0 引言

目前几内亚湾区域物流系统尚不完善，如无水港的选址与建设。无水港是物流运输中的重要一环，能为中国港湾区与西非区域的互联互通提供决策支持。目前，已有文献[1-4]通过对无水港运输网络进行研究，分析无水港运输过程中涉及的成本，以总成本最小为目标构建无水港选址模型，包含建设、运输、堆存、时间成本等。此类模型适用于信息完善的无水港选址，详细的成本分类能提升模型的准确、可靠性，但模型包含大量假设。在信息匮乏地区，以几内亚湾为例，由于发展滞后，存在运输路线难以确定、以地区（如城市）为单位的物流数据难以定量的问题。成本模型的无水港选址大多属于NP-hard问题，求解精确解需要对解遍历，当问题规模过大时求解难度、时长增加。启发式算法则存在局部最优解的可能。

另有学者在无水港选址中引入评价指标，对备选城市进行筛选得到最优选址。有学者[5-8]从传统角度出发，提出了无水港候选城市的评价指标，从经济、运输等角度出发进行选址评价，另有学者[9]将复杂网络指标运用至无水港选址中，以上方法都在实例应用中证明了有效性。此外，Chang[10]在其两阶段模型中除了交通运输、地区经济外，增加了政治因素和环境因素。Lam[11]等以越南为例，提出将多标准分析方法应用于无水港选址，并提出需关注国家的特定无水港建设环境；Bian[12]认为，无水港的选址还需考虑基础设施建设、贸易水平等因素，并将建设地的客观因素考虑在内。以上研究表明了在无水港选址中需要考虑当地的客观因素。在研究地区信息匮乏时，难以确定政治、环境、基础设施方面的数据，如何应用评价标准有待研究。且无水港选址的评价标准难以统一，需要结合实际应用分析。

综上，已有无水港选址成本模型的考虑角度各有不同，模型涵盖方面广，在信息齐全地区实践时，具有一定的指导作用。然而几内亚湾发展滞后，信息获取困难，以上方法不完全适用。指标评价体系加入了定性的研究，但信息匮乏时，模型的科学性和有效性需要结合无水港选址地的客观因素具体分析。

几内亚湾区由于长期发展滞后，物流运输系统尚不完善，实际情况中难以获得与无水港选址相关的完备物流信息。基于此种情况，本文提出了基于Voronoi的无水港选址模型，利用Voronoi图对无水港备选城市进行划分，将物流需求点与备选的城市对应，排除模型在求解时的不合理情形，降低了模型求解的难度；从无水港的运输、建设、运营成本等方面出发，构建总成本最小模型，利用有限的信息确定无水港选址。此模型对于非洲等信息匮乏地区的无水港建设可以提供决策支持。

1 基于Voronoi模型的无水港选址方法

1.1 Voronoi基础理论

Voronoi图是计算几何的一个重要研究内容，定义为：n个在平面上有区别的点Xi（i=1，2，…，n），按照最邻近原则划分平面。具体为利用所有相邻点之间相连直线的垂直平分线进行划分，将平面分成n个区域，构成n个多边形Vi（i=1，2，…，n），如图1所示。其特征为：Voronoi多边形Vj内的点到此多边形Xj点的距离比到其他任何一Xi点的距离都近。

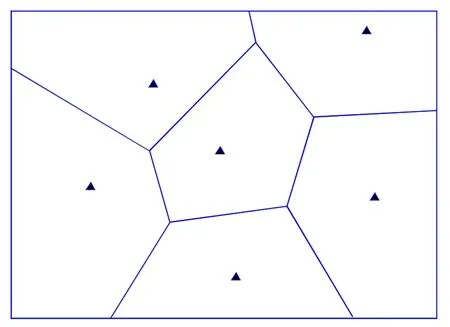
图1 Voronoi示意图Fig.1 Voronoi diagram

Voronoi图的特性适合于本研究的区域划分，具体表现为：相应的 Voronoi多边形内部的无水港备选城市到达该Voronoi多边形内部的物流需求点的距离短于该Voronoi多边形外的备选城市。

1.2 基于Voronoi的无水港选址方法框架

无水港选址方法框架如图2所示，可分为以下步骤：

确定无水港的物流需求点。以地区的年物流量作为物流运输量，以地区形心为基点，以此作为物流需求点。是地区物流运输的重心。假设所有物流都经过物流需求点。

以物流需求点为控制点，建立Voronoi图。以各个Voronoi多边形区域为界限，将位于同一多边形内的无水港备选城市划分为一组，结合Voronoi图的特性，认为物流需求点通过Voronoi多边形内部的备选城市进行运输时效益较佳。因此假设每个物流需求点的物流都通过其对应的Voronoi多边形内的无水港节点进行分配。

在无水港备选城市分组确定后，通过无水港选址成本模型求解最终无水港选址方案。

图2 无水港选址方法框架Fig.2 The framework of dry port location method

2 无水港选址成本模型

利用Voronoi将备选城市进行区域划分后，各备选城市与物流需求点形成对应关系，引入成本模型求解出最优的无水港建设方案。Voronoi进行备选城市的划分时，主要考虑运输过程中的地理因素，因此无水港选址成本模型考虑建筑、运营、运输3方面的成本。物流运输过程为：物流需求点将货物运输至无水港，再经无水港运输至海港。货物可通过不同方式经过不同无水港到达海港。考虑到地区物流详细信息获取困难，模型做如下假设：

1）模型参考信息为几内亚湾经纬度地理信息以及国家GDP、年物流量。

2）将地区的物流运输需求做统一化处理，记作物流需求点，地区物流均通过物流点进行运输。

3）在物流运输过程中（如物流需求点至无水港），只选择一种方式运输。

2.1 模型构建

基于上述假设，以无水港运输网络系统总成本最小为目标建立无水港选址模型，模型包含无水港的建筑成本、运营成本、运输成本，目标函数如下：

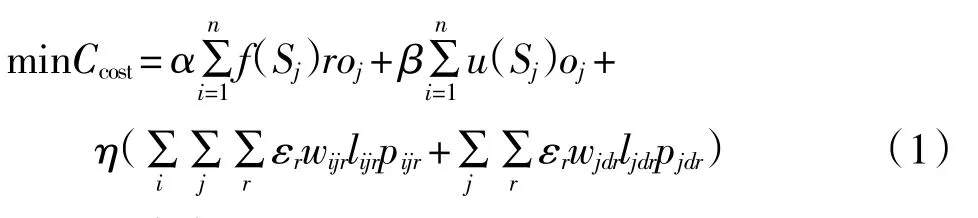
约束条件：

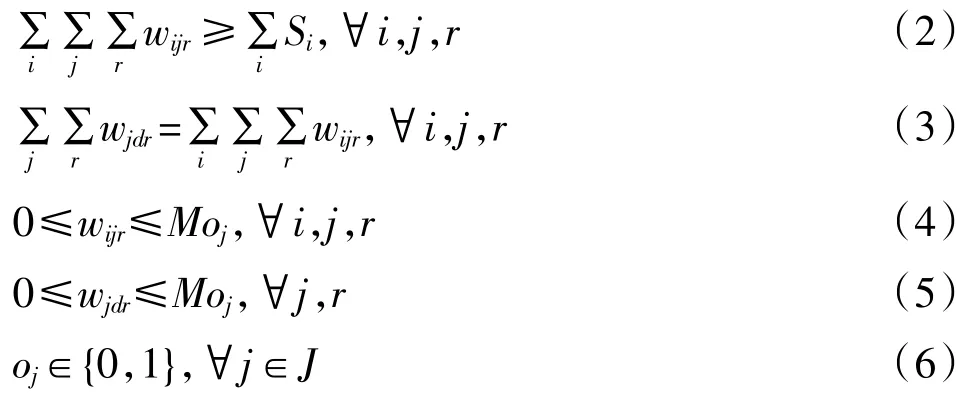
式（1）中：Ccost代表年物流总成本，由3部分组成，分别是在无水港备选城市j建设无水港的年建筑成本、年运营成本、年运输成本。

建筑成本中：Sj代表无水港i的年物流量；（f S）j代表无水港建筑成本函数；r为折旧率；oj为二项变量，当在备选城市j建设无水港时为1，否则为0；α为权重系数。

运营成本中：u（Si）代表运营成本函数；β为权重系数。

运输成本中：wijr、lijr、pijr为物流需求点i至备选城市j运用r方式运输的物流量、直线距离、单位运输费用；同理，wjdr、ljdr、pjdr为备选城市j至海港运用r方式运输的物流量、直线距离、单位运输费用；εr为运输方式r的距离折算系数，根据不同的运输方式确定；η为权重系数。

约束条件部分，式（2）保证运输至无水港的物流量大于总的物流需求量；式（3）保证运输至海港的物流量与运输至无水港的物流量相等；式（4）、式（5）保证未被选取的无水港备选城市的物流运输量为0；M为一极大的数；式（6）为对oj的阐述。

2.2 模型求解

基于Voronoi图的区域划分，设计物流成本模型求解步骤如下：

第一步，生成初始方案S。

1）随机选取每个物流需求点对应的Voronoi多边形中的一个备选城市。

2）以每个物流点的物流需求作为备选城市建立无水港的规模标准。

3）利用无水港选址成本模型来计算其成本Ccost（S）。

第二步，产生一个新的解S′。

1）对于每个Voronoi多边形，按顺序替换一个无水港备选城市，将新解S′代入成本模型计算Ccost（S′）。

2）计算值Δt=Ccost（S′）-Ccost（S），如果Δt＜0，则将新解S′作为当前解，否则，以原解S作为当前解。

第三步，当一个Voronoi多边形内的备选城市均被替换，则选择另一个Voronoi多边形，进行第二步。

第四步，如果Δt变化小于阈值或达到迭代次数，以当前解为最优解。

3 案例分析

以几内亚湾腹地为例进行分析，涉及国家15个，各国年物流运输量见表1；选取无水港备选城市43个，由于数据众多，给出部分数据见表2；海港为尼日利亚的拉各斯港，经纬度分别为6°27′47.7"N，3°24′09.7"E。几内亚湾地区示意图见图3。

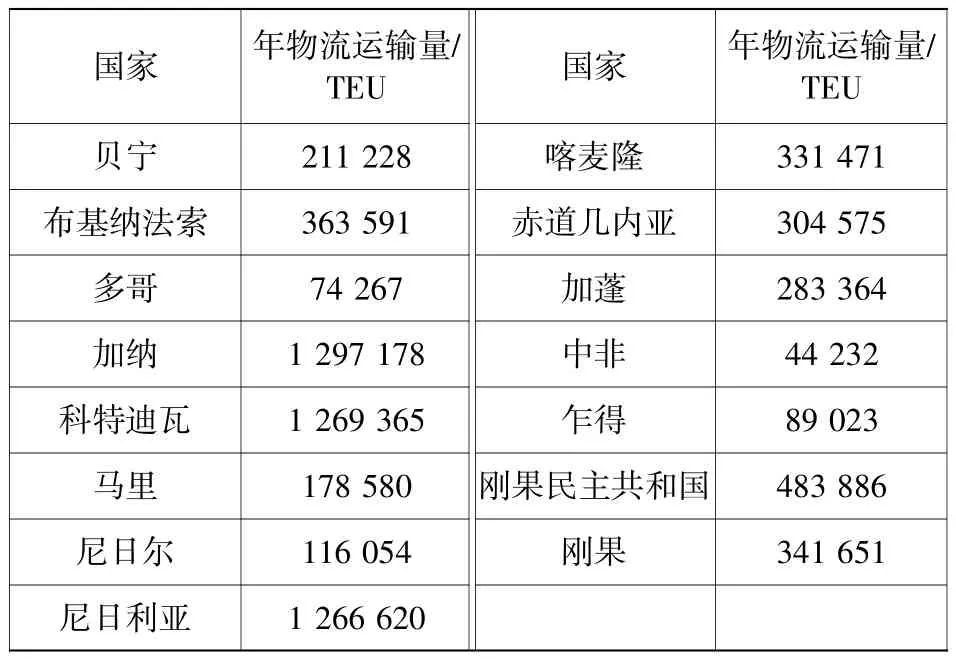
表1 国家年物流运输量Table 1 National annual logistics transportation volume

表2 无水港备选城市Table 2 Alternative cities for dry ports

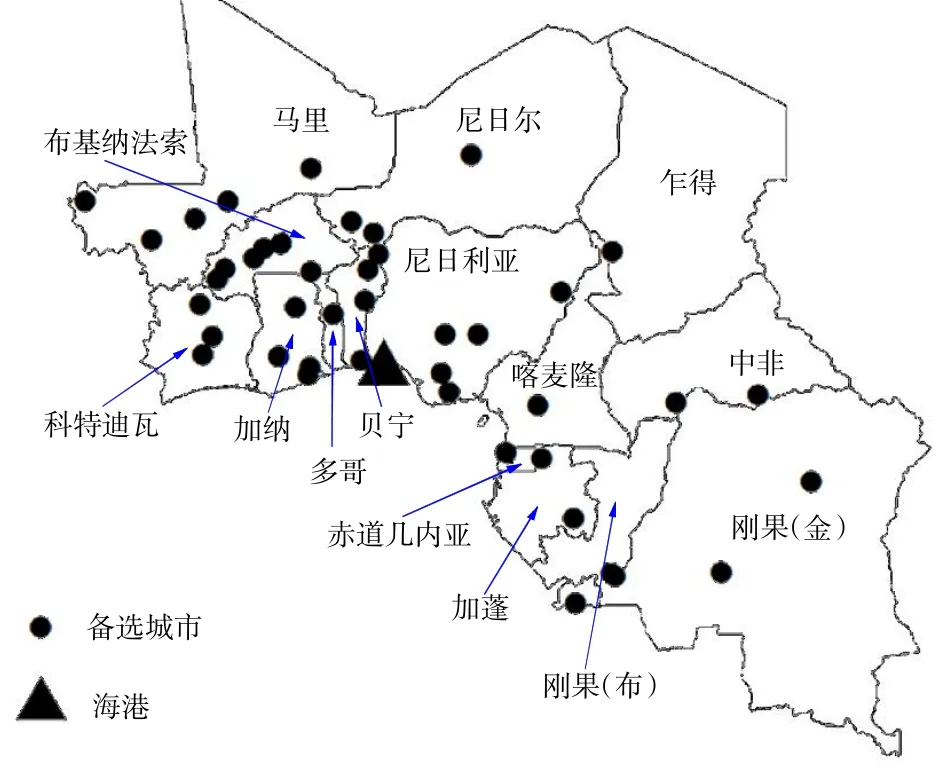
图3 几内亚湾地区示意图Fig.3 Diagram of the Gulf of Guinea region

以国家年物流运输量作为物流需求，以国家形心为基点，形成物流需求点，并生成相应Voronoi图，并将备选城市进行分组。几内亚湾区域的铁路、水路运输发展滞后，以公路运输作为运输方式，依据《国际集装箱汽车运输费收规则》，将物流运输成本中的单位运输价格设定为12元/（TEU·km）。运用经纬度信息，可以求得物流运输直线距离。建筑、运营成本方面，参考国内无水港建设数据（数据来源：《中国港口年鉴2015版》）。由于国内外差异，为使结果更为合理，按照无水港的规模等级、地区经济，设计无水港建筑、运营成本对照表。对照表见表3，其他涉及参数见表4。

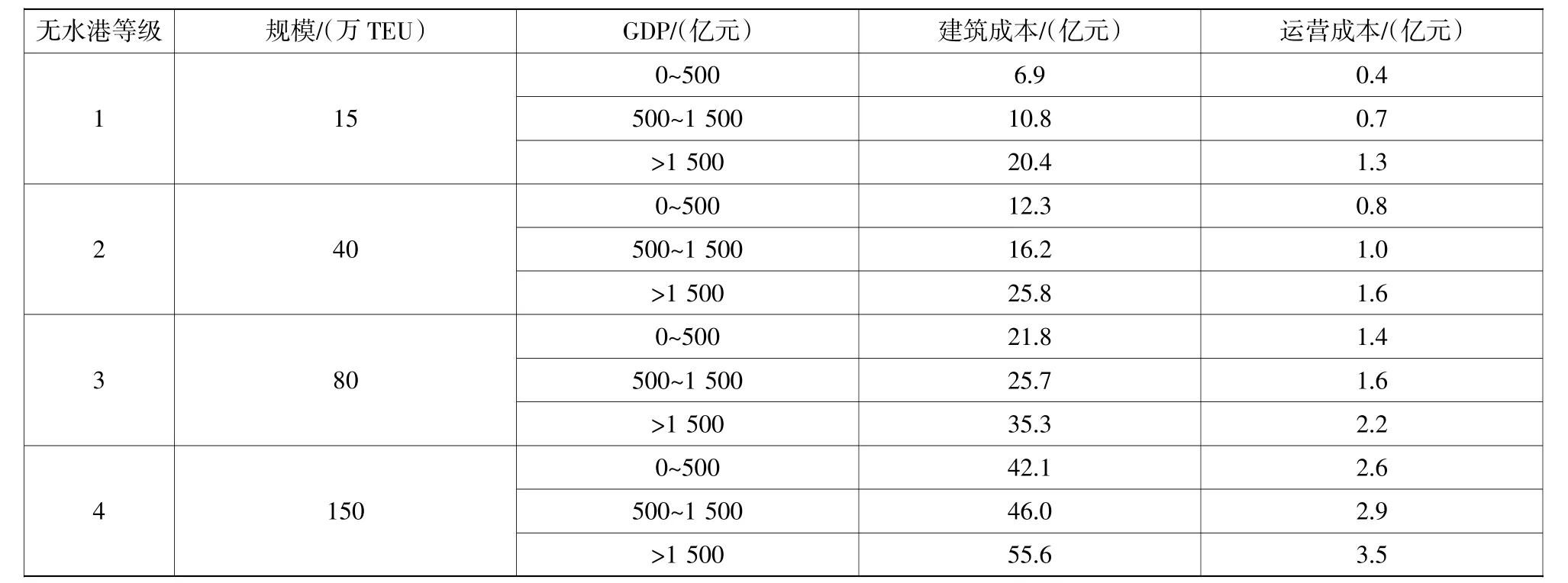
表3 无水港的建筑成本、运营成本对照表Table 3 Comparison table of construction cost and operation cost of dry port

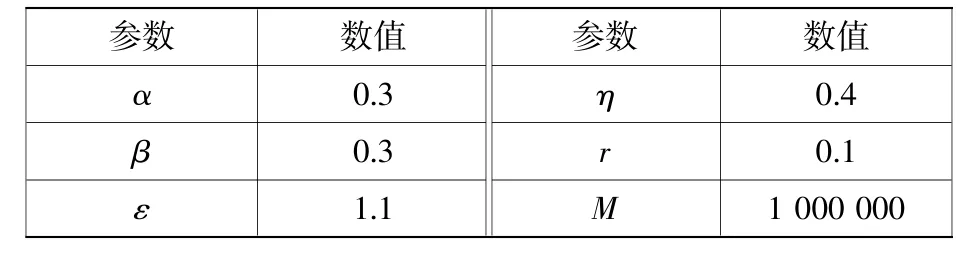
表4 参数信息Table 4 Parameter information

经过计算，选取15个城市作为无水港建设城市，选取城市为编号2、6、9、11、12、19、22、24、29、33、34、36、37、38、42。城市地理位置见图4。无水港总成本为7 214 991万元，其中运输、建筑、运营成本分别为7 019 059万元、133 400万元、62 532万元。

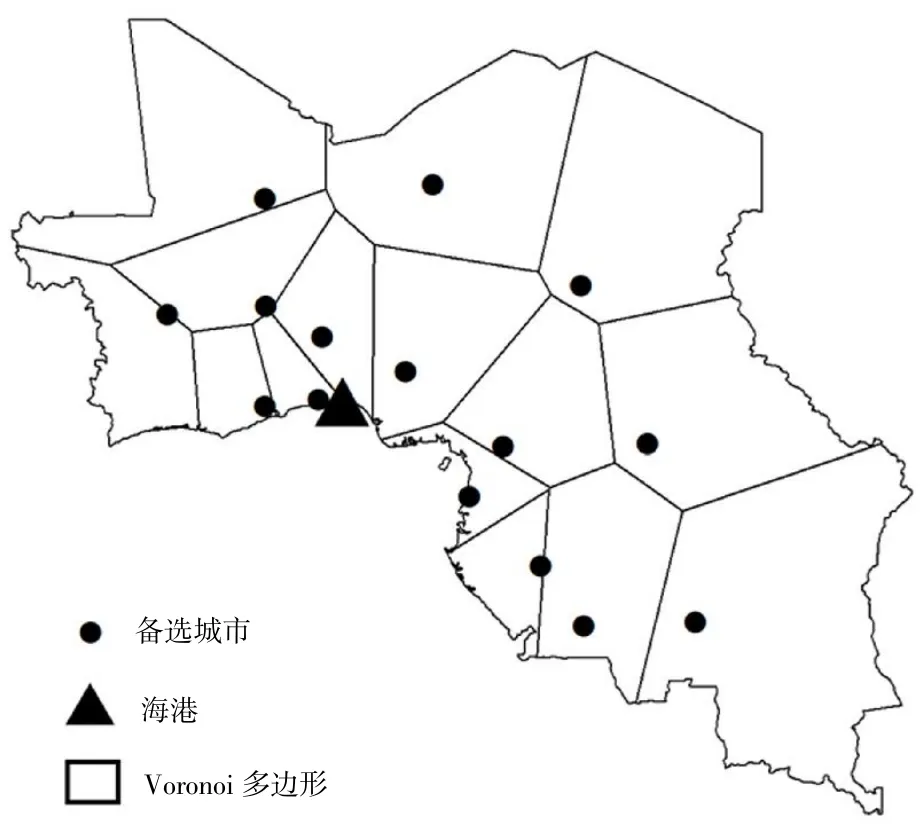
图4 无水港选址结果示意Fig.4 Dry port location result

为证明模型的有效性，运用不同选址方法进行比对。在信息有限的情况下，部分模型无法应用，以Chang[10]两阶段模型为例，其中的经济、政治、环境因素的数据缺失，无法用于案例计算。故选用P-中值法和最优选址模型[2]对西非几内亚湾无水港选址进行研究。P-中值法[13]是物流选址中的重要算法，在解决中值问题中被广泛运用；选用可行性较高的最优选址模型[4]，其考虑建筑、运输、堆叠、时间成本进行最优选址的确定。通过计算，得到P-中值法选取城市为编号5、6、8、10、11、26、27、29、37、38、41、42，最优成本为7 834 571万元；最优选址模型选取城市为编号 6、9、10、11、12、26、27、29、 37、38、41、42，最优成本为7 667 662元。将文中的基于Voronoi选址模型结果与两种方法结果进行对比，见表5。

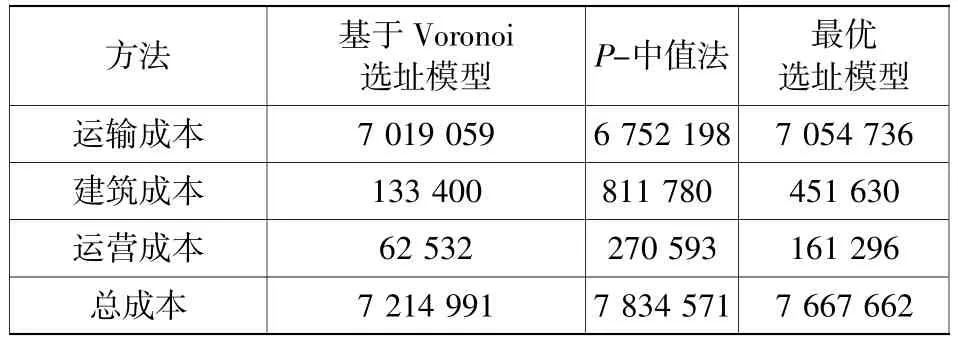
表5 选址结果对比Table 5 Comparison of location results万元

从对比表可以看到，基于Voronoi的选址模型总成本为7 214 991万元，低于P-中值法的7 834 571万元和最优选址模型的7 667 662万元，分别降低了7.8%和5.9%。P-中值法的核心是物流运输过程中距离最短，在运输成本上达到最优，但高额的建筑、运营成本使得总成本高于其他两种方法。最优选址模型考虑了建筑运营、运输、堆叠、时间成本，增加考虑因素使得模型建筑、运营成本和总成本优于P-中值法。但其中的建筑成本为定量，并未考虑由于不同地区带来的成本差异；堆叠成本与时间成本则因无法获得实际信息而只能进行一系列假设，降低了模型的准确度，使得最优选址模型各项成本相较于基于Voronoi选址模型都较高。基于Voronoi的选址模型利用Voronoi图对备选城市进行了划分，并以运输、建筑、运营成本之和最小为目标建立模型，使得其仅在运输成本上多于P-中值法，而其他各成本上均优于其他两种方法。且利用Voronoi进行区域划分后，相比于P-中值法、最优选址模型的NP-hard问题，模型求解难度大大降低。综上，模型在有效性和求解难度上均有优势，具有一定的实际参考价值。

4 结语

西非几内亚湾区的无水港选址受到物流运输系统不完善、信息匮乏的限制。因此本文提出的无水港选址模型，研究成果如下：

1）研究基于物流需求点，引入Voronoi图对无水港备选城市进行划分，通过对应物流需求点与备选城市，排除不合理的无水港备选城市选择，降低了模型作为NP-hard问题的求解难度，提升了模型的求解效率。

2）针对几内亚湾地区无水港选址信息匮乏这一问题，研究提出的无水港成本选址模型采用Voronoi图与成本模型相结合的方法，选取物流选址过程中核心的运输、建筑、运营成本。通过实例分析及与P-中值法和最优选址模型对比，表明模型具备有效性和实际参考价值，能为非洲无水港建设中制定无水港选址方案提供决策支持。