基于蒙特卡洛法的直流电子负载恒定电阻测量结果不确定度评定

李翔

（广州中广测计量检测技术有限公司，广州 510070）

引言

直流电子负载主要用于测量直流稳定电源的常用设备量，直流电子负载模拟为电阻的工作模式。在此模式下，电流服从欧姆定律随着输入电压的改变而改变[1]。为保障直流电子负载恒定电阻模式的量值的准确性需要客观合理地评价不确定度。

通常情况下，不确定度评定采用的是GUM法[2]进行不确定度评定。应用CMC法[3]需要MATLAB或VBA才能实现不确定度的评定，往往评价不确定度会比较困难。但本文通过MCM Alchimia[4]软件，使用简单、操作方便，其软件不仅可以进行CMC法的计算，也可以进行GUM分析。本文将引用MCM Alchimia 软件对直流电子负载的恒定电阻模式按CMC法进行不确定度分析，在此基础上比较，并通过MATLAB软件对MCM Alchimia的结果进行验证。

1 直流电子负载恒定电阻模式的GUM法不确定度评定

1.1 直流电子负载恒定电阻模式的测量方法

置直流电子负载为恒定电阻模式，按照图1电压测量和电流测量的方法，同时测量输入直流电子负载的电流标准值和电压标准值。

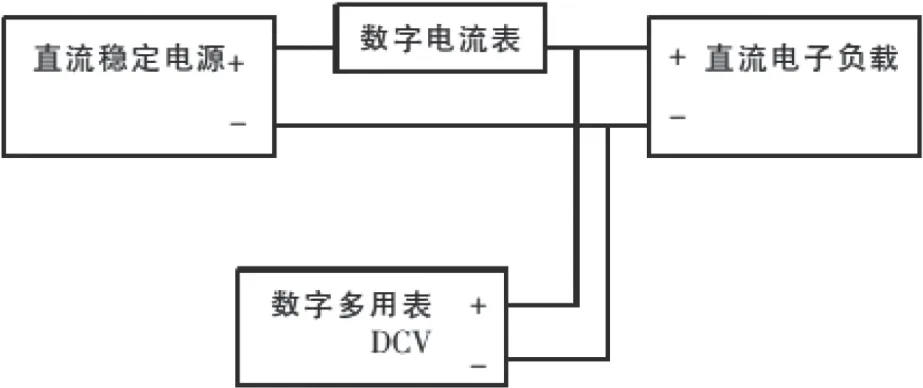
图1 测量原理图

1.2 测量模型

如公式（1）所示：

式中：

RX—恒定电阻设定值，Ω；

VS—电压标准值，V；

IS—电压标准值，A。

1.3 不确定度来源

1）由直流标准电压表测量结果重复性引入的标准不确定度u（V1）。

2）直流标准电压表不确定度引入的不确定度分量u（V2）。

3）直流稳定电源电压稳定度引入的不确定度分量u（V3）。

4）由直流标准电流表测量结果重复性引入的标准不确定度u（I1）。

5）直流标准电流表最大允许误差引入的不确定度分量u（I2）。

6）直流稳定电源电流稳定度引入的不确定度分量u（I3）。

由于各分量各不相关，因此直流电子负载恒电阻测量的合成不确定度uc，见公式（2）

其中：

1.4 标准不确定度的评定

1.4.1 由重复性引入的标准不确定度

设定恒阻模式为1 Ω从零开始调节直流电源的电压，使直流电子负载吸收的功率接近该量程满功率的 10 % 或略高于最低工作电压进行校准。同时记录直流标准电压表的值和直流标准电流的值。以设定恒定电阻1 Ω为例，重复性条件下进行10次连续测量，电压测量结果（单位：V）为：10.011、10.013、10.011、10.012、10.010、10.012、10.013、10.012、10.011、10.010。电流测量结果（单位：A）为：10.015、10.013、10.012、10.012、10.016、10.012、10.013、10.012、10.011、10.014。直流电压测量结果的平均值：10.011 5 V，直流电流测量结果的平均值为：10.013 0 A。

直流电压单次测量的标准偏差：

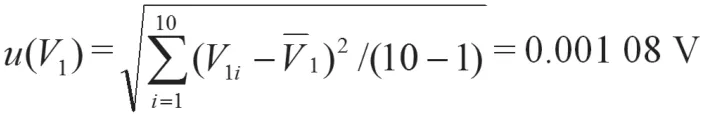
直流电流单次测量的标准偏差：

1.4.2 由标准器引入的不确定度

通过查询直流标准电压表的说明书，在10 V时的绝对不确定度为：U=0.003 5 %×读数+0.000 5 %×量程，k=2即：U=3.5×10-5Vx+5×10-5V，k=2。故：

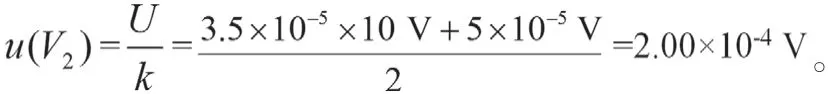
通过查询高精度交直流电流表，在10 A时的最大允许误差为：0.02 %×读数+0.004 %×满度，服从均匀分布，其包含因子故：

1.4.3 由直流稳定电源稳定性引入的不确定度

参照直流稳定电源的技术指标，其电压输出的稳定度为 ±0.01 %，电流输出的稳定度为 ±0.05 %，估计为

1.5 合成标准不确定

合成不确定度汇总表如表1所示。

合成标准不确定度：uc=0.000 386 Ω。

1.6 扩展不确定度

取k=2，则扩展不确定度

因此在恒定电阻模式设定1 Ω的测量结果为：

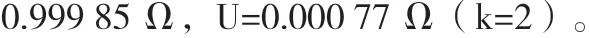
表1 合成不确定度汇总表

2 直流电子负载恒定电阻测量结果的MCM法的不确定度评定

MCM Alchimia是一款免费的基于蒙特卡洛模拟的通用的不确定度评定软件，我们使用该软件对直流电子负载的恒定电阻模型的测量结果不确定度进行评定。

2.1 数学模型

根据1.3中对不确定度来源的分析，得到测量模型如公式（2）所示。

按照MCM Alchimia软件的输入顺序进行填写，将表2中的信息填入SIMULATION DATA中，如图2所示。

图2 MCM Alchimia操作图

设定蒙特卡洛抽样次数为140 000次，置信水平p=95.45 %（k=2）进行模拟，按START SIMULATION得到直流电子负载恒定电阻的标准测量不确定度为0.000 74 Ω，包含概率95.45 %，包含区间为[0.999 11，1.000 59] Ω（见图3）。

表2 测量模型公式（2）的输入量Xi及其服从的PDF

图3 RESULTS中MCM法和GUM法的分析结果

表3 几种方法得到比较

图4 自适应CMC法(matlab软件)与MCM Alchimia软件概率分布的对比

3 几种方法分析的比较

为了验证MCM Alchimia软件的可行有效，应用MATLAB软件[5]对MCM Alchimia软件的结果进行验证，验证的结果如表3所示。为了有助于相互间比较，不确定度的分析结果保留到三位有效数字。

表3分别按照GUM法、 GUM法（MCM Alchimia软件）、CMC法（MCM Alchimia软件）、自适应CMC法（matlab软件）、MCM验证GUM法（matlab软件）进行分析：

1）首先对比GUM法，MCM Alchimia软件中的GUM法中的数据与GUM法计算结果是一致。

2）通过比较CMC（MCM Alchimia软件）与自适应CMC法（matlab软件）中的数据的对比，各组数据基本一致。对比输出量概率分布图（图4所示），两个图像基本一致。通过对比表3第4列和第5列的测试用时可知，同样运行14×104次试验，用MATLAB需要运行6.69 s，而MCM Alchimia软件仅需要0.02 s，很明显MCM Alchimia软件测试效率更高。

3）我们依据JJF 1059.2-2012用蒙特卡洛法验证GUM法的步骤验证其结果。我们用GUM得到的不确定度U=77×10-5Ω，c=5，l=-5，δ=1/2×10-5=5×10-6。通过表3第6列，发现dlow、dhigh的值均大于数值容差δ，因此GUM法不能通过验证。GUM法得到的不确定度评定结果无法得到有效验证，主要原因是电子负载恒定电阻测量模型的非线性造成的。因此，用蒙特卡洛法的不确定度评定结果更为可靠。

4 结束语

通过用MATLAB软件的验证，可以证明用MCM Alchimia软件进行CMC法评价不确定度是可行有效的。

因此应用MCM Alchimia软件可以快速得到MCM和GUM法的不确定度评定的结果，可有效提高不确定度评定的效率，降低在运算错误导致评定不确定度评定所产生的风险。尤其在非线性模型进行不确定度评定时，建议采用MCM Alchimia软件对MCM和GUM两种方法进行比较，最终得到准确可靠的不确定度评定的结果。

附MCM验证GUM法的matlab程序