基于“R-L”技术的风电系统可靠性预测分析

秦小滨，彭超

（重庆市万州职业教育中心,万州 404500）

引言

随着化石能源的日益枯竭和环境问题的日益严峻，煤炭、石油等传统能源已经不能满足未来社会发展的需求。大力开发以风电、光伏为代表的可再生能源，构建绿色高效的能源网络已成为能源行业的未来发展趋势[1,2]。风电作为一种常见的可再生能源，因其无污染、储量大、成本低等诸多优点，近年来得到了快速发展。截止2017年年底，全球并网风电总装机容量已超过500 GW，并将在2021年末超过800 GW[3,4]。

大力开发风电已成为能源板块调整的重要环节。然而，风电具有明显的间歇性和波动性，随着风电装机容量的提高，其大规模并网造成的风电并网输出电能质量低、功率波动大等问题严重影响了电网的安全稳定运行[5-7]。有效的风电出力预测可以为未来风电系统的出力提供有效的预报信息，是风电系统调度技术中的重要组成部分。因此，为了实现风电的大规模并网，有必要考虑风电系统中存在的各种不确定性因素，对风电系统未来某段时间的出力进行有效预测，并以此为依据实现对系统运行可靠性的正确评估。

目前已有大量关于风电出力预测的方法，如：人工神经网络[8]、支持向量机[9,10]、证据理论[11]等。尽管如此，由于风电输出功率受到所在地形地貌、风机布局、风机特性等多方面的因素，现有的风电出力预测方法难以实现高精度的预测结果，风电出力仍然具有显著不确定性，而这些不确定因素也往往影响着风电系统的可靠性。概率分析方法是一种有效的不确定因素处理方法，通过对不确定因素的历史统计数据的分析，能够有效识别它们的概率分布。更为理想的情况下，合理的应用概率分析方法，可以对能源系统的未来运行状态进行模拟，以评估系统在未来时间内的运行可靠性，实现对故障风险的有效预防。

现有关于风电系统的可靠性预测所考虑的不确定因素主要集中于风机与电网之间的能量交换过程。而未充分计及系统中存在的其它不确定因素，这在一定程度上限制了对系统的可靠性评估，甚至忽略系统中潜在的危害。“R-L”作为一种风险分析技术，采用参数电阻（R）和负荷（L）刻画系统的运行状态，目前已在多个工程、非工程领域实现了可靠性评估，如：工程系统中的结构可靠性评估、证券市场交易、通信网络的评估等[12]。本文充分考虑了风电系统风电出力和负荷的随机性，应用“R-L”技术，将总发电量视为系统中的电阻参数R，用电负荷作为系统中的负荷参数L。当系统满足R＞L时，则认为该系统是可靠的。通过历史数据的采集和模拟，分析风电系统在未来时间内的可靠性（即事件R＞L的概率，P[R＞L]）。基于某一风电场的实测数据进行仿真分析，结果验证了所提方法的正确性和有效性。

1 “R-L”技术

采用“R-L”技术进行可靠性预测的主要思路为：

1）确定系统中存在的不确定因素；

2）通过对上述不确定因素的历史数据进行统计和分析，确定大致的概率分布类型（如：正态分布、Weibull分布等）；

3）计算上述概率分布函数的具体参数；

4）确定系统中的参数R和L；

5）计算系统的可靠性方程，即P[R＞L]，其中，P[·]表示某事件发生的概率。

需要说明的是，对于系统中的风速、线损以及用户负荷等变量，可基于图像分析技术，如：直方图、概率图等方法建立其相应的概率分布函数；而对于参数R和L，需基于上述变量的分布参数，采用模拟方法进行建模。

1.1 参数R的建模

对于风电系统，参数R可用过去某一年的总发电量表示。基于风速（v）和系统损耗（loss）的概率模型，可以获得相应的R值。首先介绍v的概率分布函数的求解方法。

一般而言，可根据历史风速数据模拟得到风速的概率分布。现通常采用双参数Weibull分布刻画风速的不确定模型，其累积分布函数如下：

式中：

F(·)—累积概率分布函数；

v—风速变量；

f(·)—概率密度分布函数；

c、k—Weibull分布函数的参数。

若对F(v)取两次自然对数处理，则式（1）转换为如下形式：

通过以上处理方式，式（1）可转换为形如y=ax+b的线性表达式（式（2））。若以ln{-ln[1-F(v)]}为输出变量y，以ln(v)为输入变量x，则可以计算得到Weibull分布参数的表达式：

F(v)可基于历史统计数据模拟得到，具体方法如表1所示。其中，n是历史数据数目，vx为序列为x的风速实际大小，所有的历史数据从小到大排列。

在确定Weibull分布参数后，便可通过随机生成变量样本和反变换，生成更多新的风速样本。具体步骤为：生成服从均匀分布的随机数u，满足0≤u≤1，与概率值u相对应的风速大小可由以下逆变换计算得到：

由于u满足位于区间[0，1]上的均匀分布，相应地，(1-u)也可视为位于[0，1]的均匀分布变量。则上式可以改写为：

以上是获取风速v的概率分布函数的大概原理。类似地，基于风电场损耗loss的历史统计数据，也可以建立其相应的概率模型。

基于上述风电系统损耗和风速的模拟数据，可以计算得到风电场每小时产生的电功率为PNet(h)。假设风电系统中的风力涡轮机数目为NT，PNet(h)的计算公式为：

式中：

表1 F(v)的模拟方法

Pout—单个风力涡轮机输出的电功率，其大小与风速、空气以及涡轮机特性等因素相关；

Tloss—经模拟得到的风电系统总功率损耗。

Pout可由以下方程求得：

式中：

A—涡轮机的扫掠面积；

ρair—空气密度；

Cp—功率系数；

v—经模拟得到的每小时风速值。

总功率损耗Tloss由多部分构成：

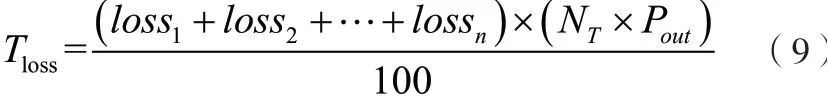
式中：

loss1，···， lossn—系统各方面的损耗，如：由涡轮机故障、传输损失，以及尾流引起的功率损失等。各类损耗所占的百分比均以通过测量得到。

如前文所述，参数R表征风电系统的年发电量，即一年中各小时发电量的总和：

结合概率统计相关知识，可以得到R的均值μR和标准差σR：

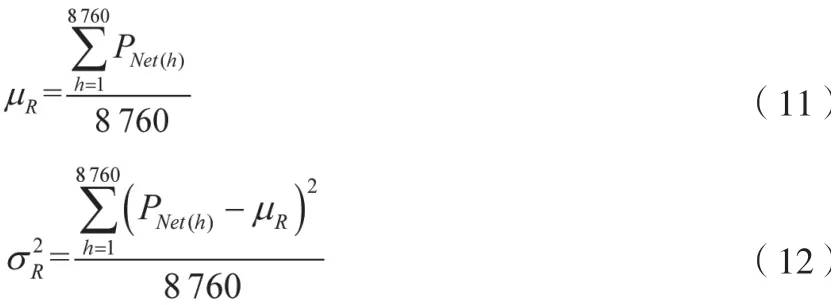
1.2 参数L的建模

在风电系统中，通常认为负荷服从正态分布或者对数分布。本文暂不考虑负荷与风速之间的相关性，因此可以对负荷单独进行建模。负荷模型的建立往往需要大量的历史统计数据，本文采用Box和Muller转换方法刻画负荷的正态分布模型。若变量Y服从对数正态分布，则始终满足以下情况：若变量Y的均值为μ，方差为σ2，则eY也服从对数正态分布，且有均值为μ，方差为σ2。

在风电系统中，参数L可由年度总负荷值表示，与公式（10）类似，采用采用Lh（每小时负荷模拟值）代替PNet(h)，即可得到参数L关于Lh的表达式。此外，与式（11）和（12）类似，采用L代替R，Lh代替PNet(h)，以及μR代替μL，可以计算得到参数L的均值和标准差。

需要注意的是，对于参数R和L的均值和方差的自然对数可以通过它们的对数正态分布函数获得，标准差r可直接由方差的平方根计算得到。

1.3 P[R＞L]的求解

如前文所述，系统的可靠性指标可由事件R＞L发生的概率，即P[R＞L]表示，其定义如下：

式中：

fRL(r, l)—参数R和L的联合分布函数，具体可以写为：

fRL(r, l)一旦确定，系统可靠性指标便可以通过数值积分估算得到。构建fRL(r, l)具有较大的难度，需要在获取大量统计数据的基础上，绘制相应的二元直方图，进而建立相应的联合分布。为简化计算过程，假设R和L之间相互独立，则联合分布函数则可以简化为以下形式：

由于R和L相互独立， fRL(r, l)可以简化为各单变量分布函数的乘积。由于单变量分布函数所需要的统计数据较少，采用式（15）的表达形式有效降低了求解难度。基于以上假设，系统的可靠性指标可以改写为：

对于参数R和L，若它们均服从正态分布或者对数正态分布，则事件R＞L可以等价为如下情况：

1）若R和L均 服 从 正 态 分 布，则R＞L等 价 为R-L＞0；

2）若R和L均服从对数正态分布，则R＞L等价为R/L＞1。

令事件R＞L为X。对于第一种情况，当R和L服从正态分布时，X的均值和方差为：

系统可靠性指标可由如下方程估计：

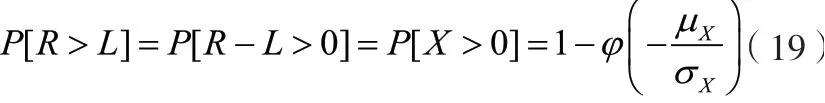
式中：

φ(·)—标准正态分布变量的累积概率函数。其数据可由正态分布概率表查阅得到。

类似地，对于第二种情况，若R和L服从对数正态分布，令事件X为[R/L]，则其均值和方差可写为如下形式：

系统可靠性指标可写为：

式（19）和（22）分别表示R和L服从不同分布函数的情况下，系统可靠性指标的表达式。

2 算例说明

为验证所提可靠性预测方法的正确性和有效性，以某海岛的实测历史数据为例进行仿真说明。该海岛上具有装机容量为12 MW的风电场，包含四个额定容量为3 MW的风力涡轮机。其它数据说明如下：

1）气候环境说明

采用风速统计数据，数据量测点海拔为20 m。从历史数据中，统计出风度与海拔高度的关系：

式中：

v—与海拔高度h对应的风速（80 m，即为涡轮轮毂的高度）；

vref—在参考海拔高度href处的风速参考值（href=10 m）；

α—风切变，取0.2。

2） 风电场实测数据说明

本文选取了该风电场在2013至2017年间，连续五年内每小时的用电负荷数据，以及2017年内每小时的风电输出数据。

3） 风电系统损耗说明

在风电系统的实际运行过程中，其能量的损耗来源于多个部分，基于历史统计数据，本文给出了在风电系统中各部分损耗所占发电量的比例，具体见表2。

表2 风电系统中部分损耗的比例

3 算例分析

算例分析的主要思想为：①基于已知的历史数据，模拟该风电系统2017年的发电量和用电负荷数据，并以实际数据进行比较，以此来验证所提预测方法的正确性；②在1）的基础上，估算未来一年内风电系统的可靠性指标（P[R＞L]）。在建立不确定因素概率分布函数时，风速基于其月度历史数据，而用电负荷基于其年度历史数据。

3.1 预测方法验证

基于对风速历史数据的统计和分析，发现风速服从Weibull分布。以2014年12月的风速作为示例，采用直方图和QQ图显示统计结果，如图1和图2所示。图2和相应的假设检验结果验证了风速服从Weibull分布。

在此基础上，采用公式（3）和（4）计算了Weibull分布函数中的参数c和k，参数计算结果的实际值和预测值如图3所示。以2013至2016四年内每个月的风速统计数据为基础，计算四年内每个月Weibull分布参数的平均值，以此作为实际值。采用Excel内置的随机数生成器和公式（6），基于历史风速数据以及Weibull分布参数c和k的平均值预测了2017年的每小时风速，预测值和实际值的分布情况如图3所示。由图可见，所提预测方法具有较高的精度。

图1 风速历史数据直方图

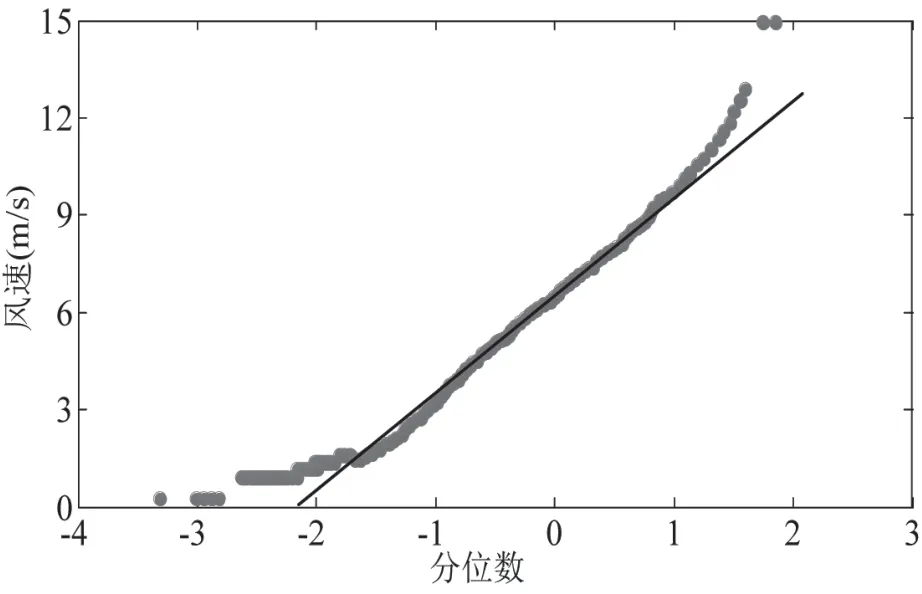
图2 风速QQ图

图3 2017年风速Weibull分布参数计算结果

在获取风速的概率分布函数和预测值后，可采用式（8）计算单个风力涡轮机的输出电量Pout，式（8）的各参数为：A=6 300 m2，ρair=1.230 kg/m3，Cp与风速实际值有关。采用公式（7）计算系统每小时发电量PNet(h)，采用公式（9）计算系统的总损耗Tloss。最终采用公式（10）计算参数R。表3给出了基于历史数据和所提方法得到的2017年最大风速、峰值负荷以及参数R的预测值和实际值之间的结果比较。

基于2013年至2016年间的负荷历史数据，建立其分布函数，并得到2017年的参数L。由于负荷的数据以年为单位进行统计，以其中某一年为例，图4显示了2014年的负荷直方图。与参数R的预测过程相似，建立负荷的直方图和QQ图分析负荷服从的具体分布及参数（经仿真分析验证了负荷服从正态分布），基于Excel生成随机数模拟2017年的负荷数据。表4比较了负荷的预测值和真实值。

由表3和表4可知，无论是对于参数R还是L，预测值与实际值之间的相对误差绝对值均能够保持在2%以内，这验证了所提方法具有较高的精度。

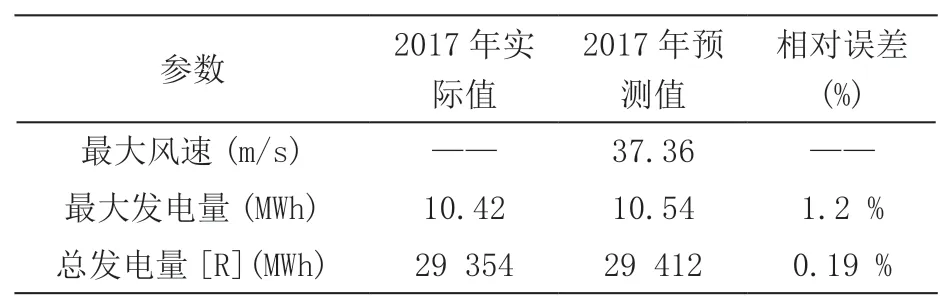
表3 2017年风速和发电量预测结果

图4 2014年负荷直方图

表4 2017年参数R和L预测值和实际值比较结果

3.2 P[R＞L]的计算

对于未来某一段时间内风电系统的可靠性，均可以由参数R和L的预测值计算得到。为计算P[R＞L]，本文基于2013年至2016年这五年的历史统计数据预测未来时间内的R和L参数。假设在预测时间内，风电系统的负荷和总装机容量保持不变，基于上一节的内容获取了过去五年内，每个月的风速所服从的Weibull分布参数平均值，具体见表5。

假设风电系统的损耗服从正态分布，基于现有每小时风电系统的输出电量数据，将以表2中的占比计算得到的损耗作为均值，采用蒙特卡洛模拟法处理其不确定性。分别假设损耗的变异系数（Coefficient of Variation,Cov）为5 %、15 %和25 %。由表2可知，风电系统的损耗可分为六种，由于loss2和loss2所占比重很小（不超过1 %），因此在模拟过程中可近似认为它们的数值大小不变。以每小时的风电系统损耗作为变量，表6给出了三种情况下，风电系统的损耗、发电量以及参数R化对系统可靠性的影响要远远大于损耗变化的影响。从另一方面理解，P[R＞L] 越高往往说明了系统在某一年内满足负荷需求的可靠性越高。

表5 2013～2016年每月风速的Weibull分布参数平均值

表6 风电系统损耗、发电量以及参数R的统计结果

4 结论

风电作为一种绿色、环保的可再生能源，推动其开发和利用在为能源产业同时带来了机遇和挑战。现有风电场馈入电网的最大问题仍然在于风电的不确定性对电的统计情况。

表7 不同负荷水平下的P[R>L]

以上是风电系统在不同波动情况下对参数R的预测情况。对于参数L，其可由风电系统的总负荷表示。根据2013年至2016年四年内的负荷历史数据，可得四年间负荷服从正态分布，且均值和标准差分别为μL=13.52 MWh和σL=2.85 MWh，四年内参数L的均值为118 214 MWh。

至此，参数R和L的概率分布和预测值均已得到。由于R和L均服从正态分布，可通过公式（19）计算得到P[R＞L]。查找正态分布概率表获取所需要的φX值。经过仿真运算，参数R的均值和标准差可由表6查得，参数L的均值和标准差也可采用类似的方法，最后算得μL=12.98 MWh和σL=2.85 MWh。表7给出了在不同的变异系数下，负荷水平分别取均值的100 %、75 %以及50 %这三种情况时，计算得到的P[R＞L]。

P[R＞L]表征了在给定条件下（风速、负荷以及系统损耗），风电系统所具有的可靠性。P[R＞L]的数值越大，表明系统可靠性越高。由表7可见，当取负荷水平逐渐降低时，系统的可靠性逐渐增加。保持负荷水平不变，当系统损耗的变异水平由5 %增长至25 %时，P[R＞L]的数值基本上保持不变，这表明在风电系统中，负荷变力系统安全运行造成的隐患。鉴于风电系统可靠性的需求，本文提出了一种风电可靠性预测方法，基于大量历史数据，同时考虑了风电系统出力和用电负荷的不确定性，采用R-L技术对风电系统负荷和发电量进行预测，进而构建系统的“R-L”模型，以实现对未来时间段内风电系统可靠性的评估。以某一实际风电场为研究对象，通过算例仿真和比较，可以验证所提模拟预测方法可以实现在未来时间段内对风电出力及用电负荷的正确预测，而R-L技术可以实现对风电系统可靠性的有效评估。