温度梯度荷载作用下CRTSⅡ型轨道板变形差异分析

许振楠 卜建清 张吉仁

(1.中土集团福州勘察设计研究院有限公司， 福州 350013；2.石家庄铁道大学， 石家庄 050043)

CRTSⅡ型板式无砟轨道是我国对德国博格板式无砟轨道系统引进、消化、吸收、再创新的成果之一，被广泛应用于我国华中、华东等地区的高速铁路。

太阳辐射、空气对流等作用在混凝土轨道板内部形成了复杂的温度场，因混凝土导热性较差，沿轨道板厚度方向会形成温度梯度，从而引起轨道板上拱或翘曲变形，改变轨道结构的几何形位，进而影响列车运行的舒适性和安全性。目前，关于轨道板温度场的研究已比较全面[1-3]，综合各地的实测温度数据，发现轨道板温度横竖向方向均呈现出明显的非线性特征，其竖向温度梯度分布符合指数分布规律[4-5]。然而，我国TB 10621-2014《高速铁路设计规范》[6]给出板式无砟轨道温度荷载为线性的正温度梯度90 ℃/m、负温度梯度-45 ℃/m，并不能很好地适用于我国不同地区的气候条件。在温度梯度荷载对轨道板变形影响的后续研究中[7-8]，多数研究者为简化计算模型，以线性温度梯度荷载代替实际情况下轨道板受到的非线性温度梯度荷载。但是，关于线性与与非线性温度梯度荷载下轨道板变形的差异大小研究甚少。因此，本文通过有限元软件ANSYS建立了CRTSⅡ型板式无砟轨道结构的三维有限元模型，选取北京、上海和沈阳3个不同地区的轨道板作为研究对象，分别选取线性温度梯度荷载、地区温度梯度适用公式和实测温度数据，对模型进行计算模拟，并对轨道板变形数据进行对比研究。

1 有限元模型建立

桥上CRTSⅡ型板式无砟轨道由上至下依次是钢轨、扣件、轨道板、砂浆层和底座板，轨道纵向由6根φ20钢筋将轨道板结构连接成为一个整体。

在三维有限元模型中，钢轨可视为无限长梁，采用Beam188梁单元模拟钢轨的受力状态。其优点在于：首先，Beam188梁单元能模拟3D线性有限应变梁，且计入了剪切变形的影响，增加了翘曲自由度；其次，钢轨为不规则截面，Beam188梁单元允许自定义梁截面来满足不同的需求。

扣件提供纵横向阻力，有效地控制轨道形位，保证钢轨和轨道板的可靠联结。扣件弹性可减缓列车行驶时由动力作用带来的振动。扣件采用vossloh 300型扣件，有限元模型中采用弹簧单元模拟，单元类型为Combin14，弹簧竖向刚度为2.5×107kN/m，每块轨道板设置10个扣件，间距为625 mm。

钢轨下部的轨道板、砂浆层及底座板均为混凝土结构物，以长方体几何模型按照实际尺寸建立，并用Solid65三维实体单元进行离散化。板式无砟轨道结构详细参数如表1所示。

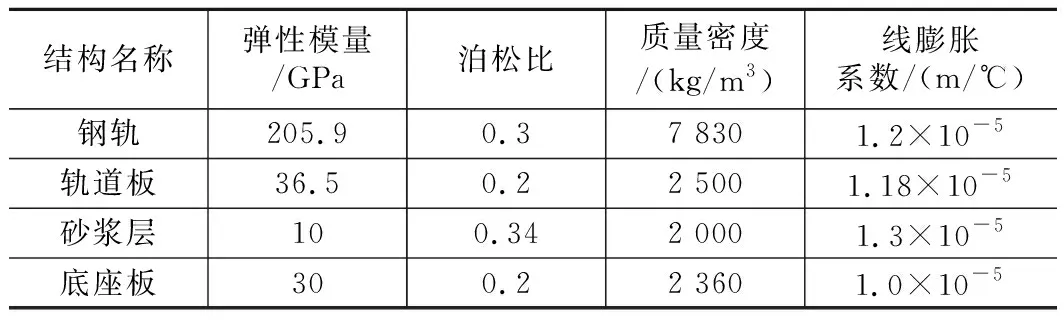
表1 板式无砟轨道结构模型参数表

为消除模型中轨道板边界效应，参照文献[9]的研究结论，建立三块纵连轨道板结构有限元模型以便更好地反映轨道板的变形情况。板与板之间6根连接钢筋以Link8杆单元模拟，并与轨道板实体单元耦合在一起，最后取中间那块轨道板为研究对象，探究其在不同工况下的温度变形。

2 荷载工况

轨道板温度梯度荷载分为两大类，一类为线性温度梯度荷载，温度梯度分布形式取规范给出的正温度梯度90 ℃/m、负温度梯度 -45 ℃/m；另一类为非线性温度梯度荷载，又分为两种，一种是各地实测轨道板温度数据荷载，另一种是采用地区非线性温度梯度分布适用公式计算出的轨道板各层温度荷载。

尤明熙等人[10]以北京交通大学轨道试验场为基础，测试出北京地区CRTSⅡ型板式无砟轨道7月份高温气候条件下的轨道板温度数据。何庆元[11]测试了上海地区某客运专线8月份高温下的CRTSⅡ型板式无砟轨道结构的温度数据。郭超等人[12]对铺设在东北严寒地区的CRTSⅡ型板式无砟轨道在夏季高温和冬季严寒最不利气温条件下的结构温度进行了监测。对3个地区24 h监测的温度数据进行汇总，如图1所示。

综合3个地区的温度数据，不难发现轨道板结构温度变化趋势整体与气温变化趋势一致，轨道板表面温度均在下午14时达到最大，底部温度均在下午16时达到最大，较表面滞后2 h。北京地区夏季高温最大正温度梯度达51 ℃/m，此时轨道板顶面温度为45.6 ℃；上海地区夏季最大正温度梯度达89 ℃/m，此时轨道板顶面温度57.6 ℃；沈阳地区夏季最大正温度梯度达64 ℃/m，此时轨道板顶面温度36.6 ℃，冬季最大负温度梯度达-30.5 ℃/m，此时轨道板顶面温度为-36.4 ℃。

闫斌等人[13-14]基于我国不同地理坐标和气候条件，引入地区调整系数，提出了适用于我国典型地区板式无砟轨道的竖向温度梯度分布公式：

图1 不同地区轨道板结构24 h温度变化曲线图

t正温度梯度=18e-6.5x+a

(1)

t负温度梯度=50x2+42x+b

(2)

式中：t——不同深度处轨道板温度(℃)；

x——距轨道板表面深度(m)；

a、b——拟合得到的正、负温度梯度的地区调整系数，我国不同地区温度梯度调整系数(部分)如表2所示。

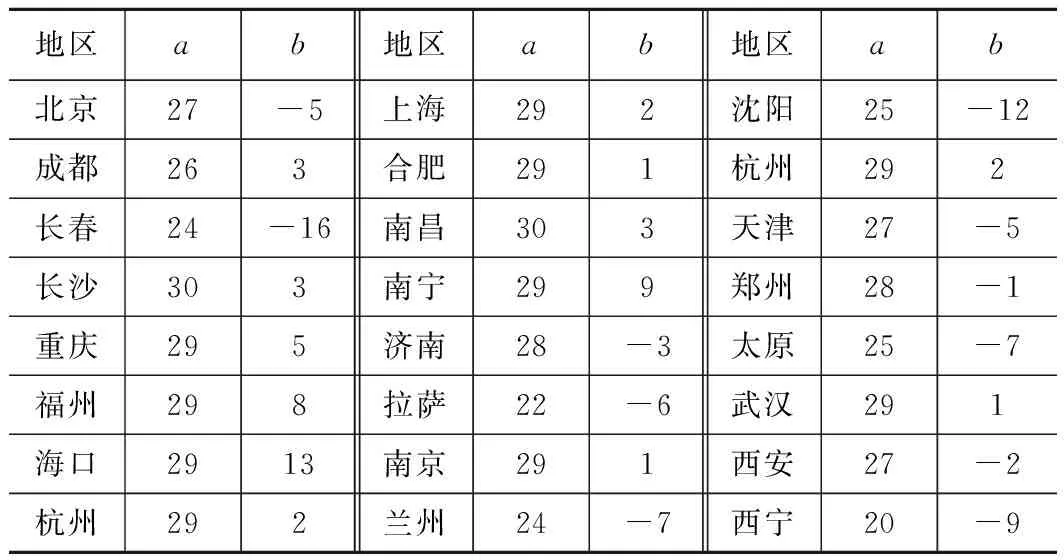
表2 我国不同地区温度梯度调整系数(部分)表

为进一步研究线性温度梯度荷载和非线性温度梯度荷载下轨道板变形的差异，同时验证适用公式的准确性，本文将北京、上海和沈阳3个地区的温度梯度分布公式提列出来，计算轨道板不同深度处的温度，并作为荷载施加到模型上。取3个地区一天中温度梯度达到最大时为最不利工况，可细分为12种工况，如表3所示。

表3 轨道板温度梯度荷载工况表

3 模拟计算与分析

板式无砟轨道在运营一段时间后，砂浆层与轨道板的黏结效果会逐渐降低，受到温度荷载作用，产生离缝、滑移等病害的几率将有所增加。为反映砂浆层的黏结状态，在轨道板实体模型和砂浆层实体模型间设置一层接触面，以Targe170和Conta174接触单元模拟接触关系，砂浆层与底座板采取共用节点的方法模拟接触关系。

施加不同荷载工况，轨道板发生温度变形。在正温度梯度荷载作用下，轨道板发生上拱变形，在负温度梯度荷载作用下，轨道板发生翘曲变形。将不同工况下轨道板变形的竖向最大位移进行汇总，如表4所示。

表4 不同荷载工况下轨道板变形竖向最大位移表

为更加直观地看出其中的差异，以每个地区为单位，将线性温度梯度荷载、非线性实测温度梯度荷载和非线性温度梯度适用公式荷载下的轨道板变形位移用统计直方图显示出来，如图2所示。

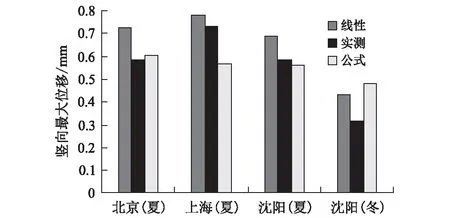
图2 各地区不同荷载形式下轨道板变形图

从图2可以看出，12种荷载工况下，线性温度梯度荷载与非线性温度梯度荷载对轨道板变形的影响确存在一定差异，这种差异既体现在数值上，又有体现在不同地区上。

对于北京地区，非线性温度梯度荷载作用下，轨道板变形较线性温度梯度荷载作用减小约19.2%。通过对工况2和工况3的结果进行对比，发现地区适用公式的温度梯度荷载与实际情况较为符合。首先是轨道板温度数值对应较好，通过地区适用公式计算出的轨道板顶面温度为45 ℃，与实际温度45.6 ℃相差无几；其次是两种情形下的轨道板温度变形也十分接近。

对于上海地区，线性与非线性实测温度梯度荷载作用下轨道板变形的差异明显减小，实际情况下，轨道板的最大正温度梯度荷载达89 ℃/m，接近于规范中给出的设计建议值90 ℃/m。通过对工况5和工况6的结果进行对比，可以看出非线性温度梯度分布适用公式已不能很好地表征该地区轨道板的实际温度情况。上海地区夏季高温最大正温度梯度情况下轨道板顶面温度可达57.6 ℃，而适用公式计算得出的板顶面温度为47 ℃，相差近10 ℃。两者的轨道板温度变形差异约为22.3%。

对于沈阳地区，在夏季高温气候条件下，轨道板变形情况与北京地区类似，线性与非线性温度梯度荷载下轨道板变形存在约14.8%的差异。非温度梯度适用公式能很好地模拟当地轨道板的变形，但采用公式计算出的轨道板各层温度值与实际测量的温度数值不太相符。通过工况10～12的模拟结果可以看出，当处于冬季严寒季节时，采用线性负温度梯度荷载与负温度梯度荷载适用公式都无法很好地表征轨道板在实际温度下的变形。

4 结论

本文通过对线性温度梯度荷载与非线性温度梯度荷载作用下轨道板变形差异的对比分析，得出以下结论：

(1)实际情况下，轨道板结构各层温度呈非线性分布，其中竖向正温度梯度可拟合成指数函数的形式，负温度梯度可拟合成二次函数的形式。

(2)线性和非线性温度梯度荷载作用下轨道板的变形存在差异，且该差异与轨道结构所处的地理位置有关，轨道结构所处地区气温越高，即轨道板顶面温度越高，线性与非线性温度梯度荷载作用下轨道板变形的差异越小。

(3)我国典型地区的无砟轨道竖向温度梯度分布公式具有较高的参考价值。该公式中，正温度梯度分布公式能够很好地表征北方地区轨道板实际温度分布下的变形，对于南方地区，由于温度升高使线性与非线性温度梯度分布下轨道板的变形差异减小，正温度梯度分布公式不够准确。负温度梯度分布公式在东北严寒地区存在较大差别，建议根据当地实测温度数据修改地区调整系数，使该公式能够更好地符合实际情况。