高陡边坡沿高程地震动响应演化规律研究

安 旭 童心豪 刘 洋 王 翔 丁选明

(1. 中国铁路北京局集团有限公司， 北京 100038; 2. 西南交通大学， 成都 610031；3. 中铁二院工程集团有限责任公司， 成都 610031；4.中铁西北科学研究院有限公司， 兰州 730000； 5.重庆大学， 重庆 400044)

由于高陡边坡结构具有规模不一、岩土体结构复杂、分布范围广、破坏程度高等特点[1]，地震往往成为其破坏触发和诱发的主要因素。2008年，汶川地震就产生了大量的地震滑坡，造成了极大的危害[2]，因此，进行地震作用下，高陡边坡稳定性的研究已经成为工程界的必要问题之一[3]。

对于边坡工程的抗震来说，地震是一个不确定性的荷载[4]，边坡在地震作用下的稳定性分析还需进行不断的理论深化研究，由于地震荷载的特殊性，常见的边坡稳定性方法难以判别和解释结构物地震稳定性及受损机制[5]。针对岩土体地震模拟的有效方式主要分为物理模型试验和数值模拟模型试验，也有部分学者采用数学模拟来研究地震，但主要在于研究宏观规律，难以具体分析特殊结构的破坏机制，物理模型试验仍是分析岩土体灾变机理及验证数值分析的最主要手段[6]。国内外发展较为成熟的岩土体地震模拟技术主要是振动台试验技术和离心机试验技术。振动台试验技术是利用激振设备、测振设备和分析设备进行原始地震动模拟的方法，已在各类地震模拟试验中取得了较为丰硕的成果。Tomaso等人[7]通过线型系统分析了振动台试验的结果和理论计算结果的对照，证实了振动台试验技术的可靠性；Biondi等人[8]通过振动台试验对钢结构模型的地震动响应结果进行了研究，并从时域和频域方向进行了相应分析；李福秀等人[9]对黄土塬边斜坡进行了振动台试验研究，并分析了其变形失稳模式；刘新荣等人[10]对顺层岩质边坡在频发微震作用下的累计损伤效应进行了振动台模型试验和UDEC离散元数值计算研究；于一帆等人[11]对玉树机场路堆积层滑坡进行了振动台试验研究，并分析了动力响应和失稳破坏机制。

振动台试验作为研究地震的有效手段，已在各种结构体系中得到了充分的验证，但振动台试验技术往往受试验模型尺寸的限制，因此需对模型进行缩尺设计与制作，尤其对以高陡边坡为代表的大型岩土体结构来说，如何考虑相似比是一个值得慎重的问题。目前，较为广泛使用的模型与原型相似比有1∶50、1∶20和1∶10，但随着振动台试验技术的发展，许多学者开始使用大比例尺的模型试验，以避免岩土体试验中的“尺寸效应”，本文从实际情况出发，以1∶10的模型与原型相似比，设计、制作了高陡边坡试验模型，边坡坡度为60°。并在地震波的加载中，采用了不同峰值加速度、不同实测类型的地震波，以考虑地震动幅值及波形对边坡沿高程的地震动响应演化规律。

1 振动台试验准备

1.1 振动台试验装置

根据模型试验的内容和研究目的，考虑振动台承载能力及相关参数，本文采用大型单向地震模拟振动台进行试验，台面结构为钢焊单层网格，振动台相关参数如表1所示。

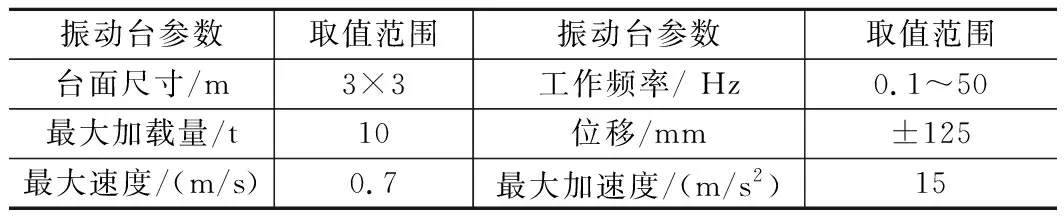
表1 振动台相关参数表

1.2 振动台相似体系

目前，针对相似定理的研究已有了较为丰硕的成果，其中相似模型试验的相似方法可使用相似三定理来实现，主要的内容包括：

(1)相似现象的相似准则相等，相似指标为1，单独参数也近似为1。

(2)在相似现象满足的情况下，实现现象的参数关系可转换为相似准则的函数关系，且与相似现象的函数式相同，也称π定理。

(3)在现象及相似现象能被同函数表达、单独参数相似且相似准则相等的情况下，两者可视为相似。

针对岩土体物理模型的相似研究也已取得了较为成熟的理论成果，本文选取的模型试验相似关系如表2所示。

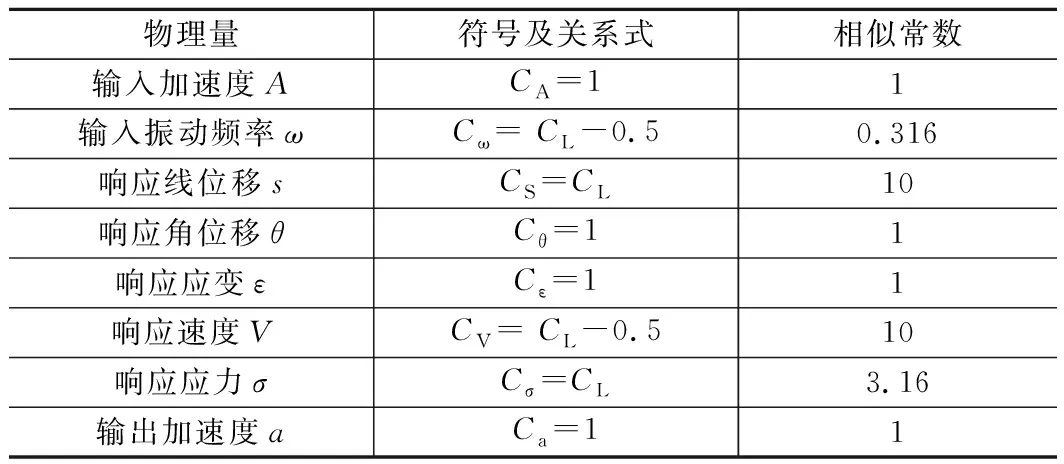
表2 模型试验相似关系表

模型总高1.5 m，其中边坡坡高1.2 m，设计坡度60°，边坡模型的底部长2.21 m，模型竖截面一致且宽为2 m，坡顶面长0.18 m。基岩高0.25 m，软弱夹层上覆在基岩上，厚度为5 cm，堆积体上覆在软弱夹层上。加速度测点布置如图1所示，其中A1、A2和A2、A3测点间的高差均为30 cm。

图1 测点布置图

1.3振动台试验的加载工况

试验采用输入加速度时程来实现地震波的模拟。根据相似原理，模型与原型的输入地震加速度时程波形完全相同，仅按照时间相似比进行调整。首先对输入地震波进行归一化处理，然后通过调节其幅值来施加不同加速度峰值的单向地震动时程。所施加的地震波类型主要有汶川卧龙地震波(简称“汶川波”)、Kobe地震波(简称“Kobe波”)和EL Centro地震波(简称“EL波”)，傅里叶谱如图2所示。地震波输入方向为沿边坡走向水平面，定义为Y向，定义垂直于水平面方向为Z向，定义边坡宽度方向为X向。此外，为了研究不同地震动加速度幅值条件下坡体的动力响应，获取坡体出现塑性变形时的临界加速度值，试验拟对模型从小到大逐级施加不同振幅的加速度荷载。

图2 加载地震波的傅里叶谱图

2 振动台试验结果分析

2.1 地震波波形对峰值加速度高程放大效应的影响

峰值加速度放大效应是研究地震对结构影响的重要参考因素之一，也是场地条件对地震动影响的代表因素。高陡边坡作为易崩塌、滑坡的结构，重点应研究其峰值加速度沿高程方向的放大效应。本文定义图1中位于自由场的加速度测点A4为基准点，分析对比峰值加速度沿高程方向的放大效应。

以测点A4为基准，首先分析位于岩质边坡内部A1～A3测点在Y向上(即边坡走向水平面方向)的峰值加速度放大效应，取边坡在输入地震动峰值加速度较小，即保持稳定性阶段的工况。当输入峰值加速度为0.1 g时，不同地震波造成A1～A3测点相对于A4测点的峰值加速度放大系数如图3所示，自下而上分别是A4测点、A3测点、A2测点、A1测点。

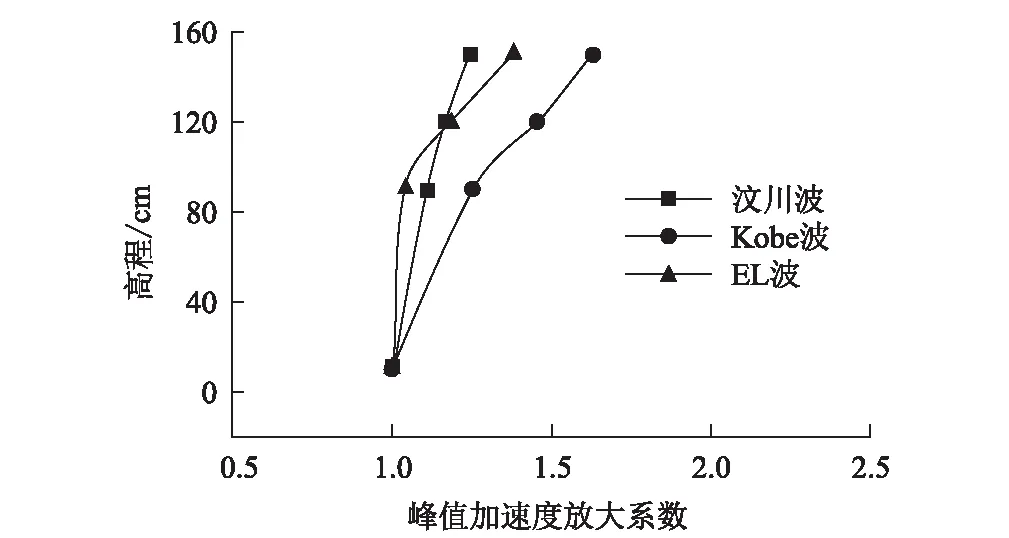
图3 输入峰值加速度为0.1 g时不同地震波峰值加速度放大系数图

从图3可以看出，在输入峰值加速度为0.1 g时，3种地震波波形造成的结构峰值加速度在高程分布上均出现放大效应，且放大系数范围均在1～1.8之间，这说明此时边坡结构处于稳定状态。但由于边坡截面自下而上从宽变窄，边坡内部的地震动响应不可避免地出现突变，因此边坡上部有较大的加速度响应。从波形对峰值加速度的影响上看，不同波形造成的高程放大效应有一定差距，其中Kobe地震波的峰值加速度放大效应较为明显，但在规律上，3种地震波造成的A1～A3测点沿高程方向峰值加速度放大效应的变化规律较为一致，均呈放大趋势，且在A3～A1测点上还呈现出较为明显的线性趋势。因此，在输入峰值加速度为0.1 g时，地震波波形对峰值加速度在高程上的放大效应上主要体现在放大系数幅值上的差异，在趋势上较为接近。

在输入峰值加速度为0.3g时，不同地震波峰值加速度沿高程上的放大系数变化规律，如图4所示。

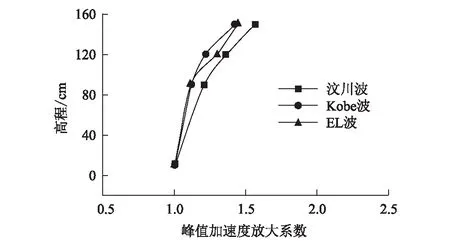
图4 输入峰值加速度为0.3 g时不同地震波峰值加速度放大系数图

从图4可以看出，峰值加速度放大系数的发展趋势仍然是自下而上增长，且放大系数的分布范围仍然处于1～1.8之间，3种地震波的峰值加速度放大系数发展趋势仍然有相似性。

综上所述，地震波波形对峰值加速度放大系数在高程上的影响主要在幅值上存在差异性，但在发展趋势上较为接近。

2.2 地震波强度对峰值加速度高程放大效应的影响

地震波强度是影响峰值加速度的重要因素，甚至是决定性因素，因此地震波强度也影响峰值加速度放大效应的变化规律。取加速度测点记录数据为Y向，以A4测点作为基准点，选取A1～A3测点与A4测点峰值加速度放大系数为研究对象。由于汶川卧龙地震波持时最长，因此，以输入不同峰值加速度幅值模拟地震波强度对汶川卧龙地震波在边坡高程上的峰值加速度放大效应进行研究，结果如图5所示。

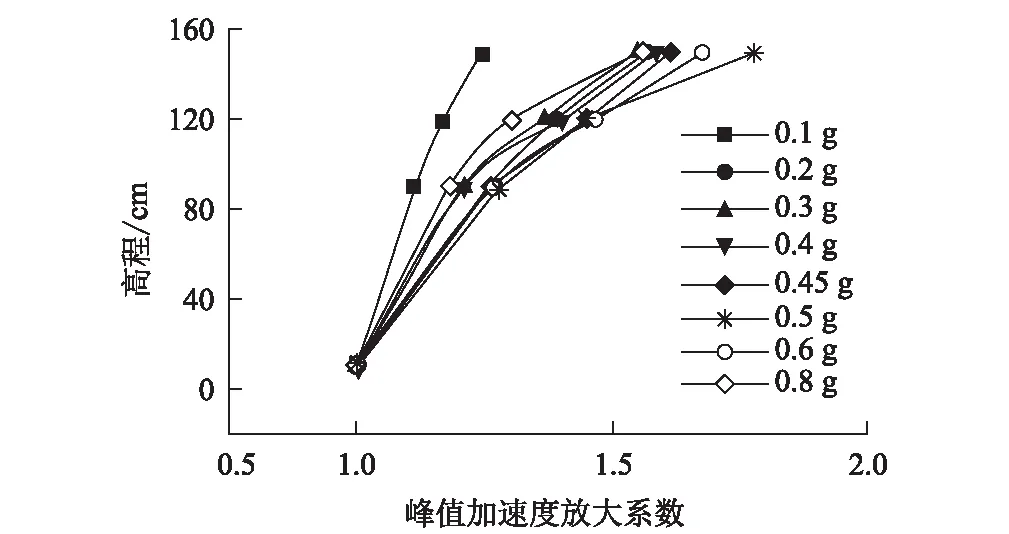
图5 输入汶川波不同峰值加速度时沿高程峰值加速度放大系数图

从图5可以看出，在A1～A3测点上，峰值加速度放大系数均与高程均呈正相关关系，且放大系数的分布范围均在1～2之间。在输入汶川卧龙地震波峰值加速度幅值为0.2 g及以防后，放大系数的增长还呈现一定的趋同性。但值得注意的是，随着输入波峰值加速度幅值的提高，同位置的峰值加速度放大系数有所增加，当输入波峰值加速度幅值为0.8 g时，沿高程走向上的加速度放大系数较输入峰值加速度幅值低的工况反而更低。这种现象大概率是由于土体的动剪切强度和动剪切模量随地震动幅值的增加而减小，因此土体的阻尼比随随地震动幅值的增加逐渐增大，使地震波在边坡结构的传递过程中出现了较大的能量损耗，从而导致加速度放大效应减弱。

2.3 不同方向峰值加速度高程放大效应

地震波在结构内部传递过程中会出现折射、反射等波动效应，因此会出现加载波在Y向，而在X向及Z向上能检测到地震加速度存在的现象(定义垂直于水平面方向为Z向，定义边坡宽度方向为X向)。地震波在Y向上的传播效应对边坡结构的整体危害性最强，但在另外两个方向上的传递规律对防止地震损坏特殊结构也有一定的参考价值。因此，在X向及Z向上，以A4测点为基准点，作出输入汶川卧龙地震波峰值加速度为0.1 g和0.3 g时A1～A3测点峰值加速度的放大系数，如图6、图7所示。

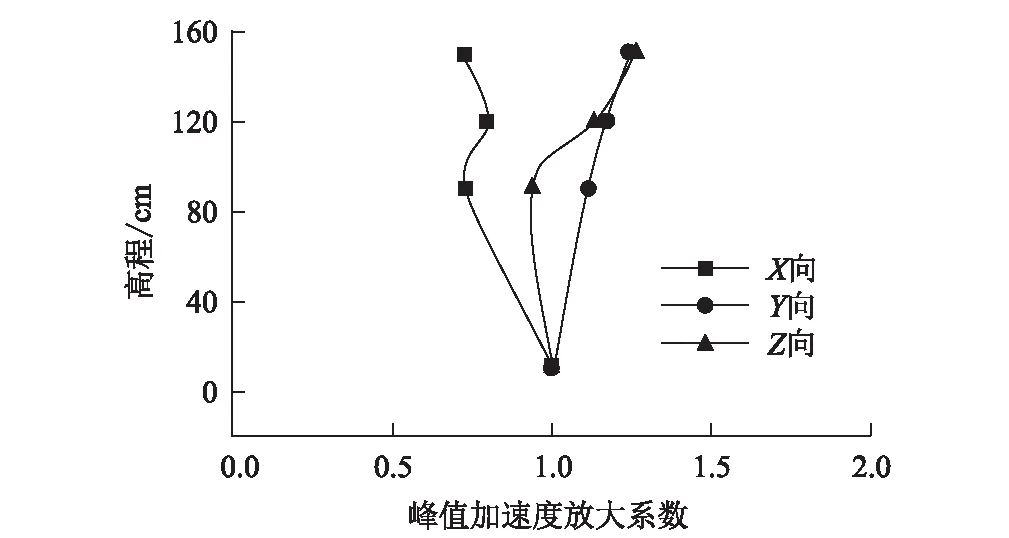
图6 输入汶川波峰值加速度0.1 g时不同方向上沿高程峰值加速度放大系数图

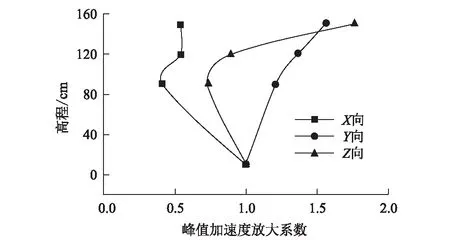
图7 输入汶川波峰值加速度0.3g时不同方向上沿高程峰值加速度放大系数图

从图6、图7可以看出，A1～A3测点在X向上的峰值加速度均弱于A6测点，这是由于试验结构在垂直于X向的截面有较好的一致性，因此峰值加速度在X向上的耗能较为明显，峰值加速度传递效应反而减弱了。这与试验模型的宽度也有影响，但对于本试验模型来说，结构在X向上的地震动响应是较不明显的。此外，A1～A3测点在Z向上的峰值加速度表达也有一定的规律性，体现在自下而上A3～A1测点的峰值加速度放大系数逐渐增大，且存在峰值加速度放大系数小于1的情况。这表明在Z向上，由于土体自重和土内粘结力，存在较大的耗能，但在边坡上部由于存在突变，因此加速度放大系数有较为明显的提升。

2.4 反映谱沿高程的演化规律

反应谱理论是体现结构动力特性与地震动特性联系的重要方法，我国GB 50011-2010《建筑抗震设计规范》中仍将反应谱理论作为求解结构地震作用的基本方法。加速度反应谱表现了单质点体系在随质点自振周期内加速度反应变化的趋势，体现了结构产生的共振效应，因此在地震动特性研究中还存在重要的参考价值。本节选取输入汶川波峰值加速度为0.1 g的地震动工况，研究结构A1～A3测点的加速度反应谱沿高程方向的演化规律。反应谱阻尼设置为0.5%，其中在输入峰值加速度为0.1 g汶川卧龙地震波时的加速度反应谱如图8所示。

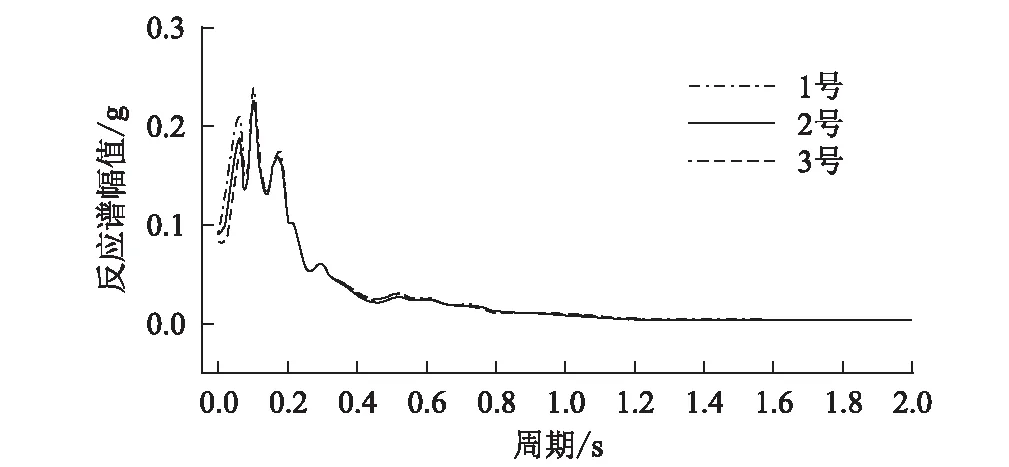
图8 输入汶川波峰值加速度0.1 g时加速度反应谱图

从图8可以看出，沿高程自下而上A3～A1加速度测点反应谱峰值对应的周期均集中0.1 s左右。随着高程的增加，在位于短周期的0.05 s附近，反应谱幅值提升，表明反应谱高频部分的幅值增加，说明边坡高程对加速度反应谱高频部分存在放大效应。

3 结束语

本文通过制作坡度为60°的高陡边坡试验模型，并在大型单向地震模拟振动台上进行试验研究，得出以下结论：

(1)地震波波形对峰值加速度放大系数在高程上的影响主要体现在变化幅值上，但发展趋势相似。

(2)不同地震波强度下峰值加速度放大系数均与高程呈正相关关系，在输入波峰值加速度较低时，同测点处地震波强度与放大系数呈正相关，但在输入波峰值加速度较高后，同测点处放大系数随地震波强度的提高反而降低，这可能是受了土体动参数的影响，且此效应在坡面上的表现更为明显。

(3)在不同方向上，峰值加速度沿高程的放大系数有较大差异，在X向上测点的峰值加速度放大系数小于1，在Z向上峰值加速度放大系数与高程成正相关。

(4)加速度反应谱沿高程的演化规律主要体现在短周期0.05 s附近，部分反应谱幅值有明显的提升效应，而在0.1 s左右的周期上变化则不明显。