基于经验小波变换的矿山微震信号识别研究

吴义文，程铁栋，易其文，赵 奎

(江西理工大学，江西 赣州 341000)

通过微震监测系统监测、分析岩体损伤破裂过程中产生的微震信号，对微震事件进行定位，进而可判断开挖过程中的岩体状态和岩体的力学行为，并估测岩体的稳定性[1]。然而矿山现场环境复杂，震源种类繁多，导致有效的微震事件中夹杂着许多干扰信号，其中爆破震动信号占比较大。信号在传播时，由于信号会在不同介质体内衰减并同时受外界因素干扰等，使得爆破震动信号与微震信号在时域波形上较为相似，而当前的微震监测系统自动识别微震信号的效果较差。若主要依靠人工方法对微震信号进行识别并处理，则经常会出现漏处理、误处理的情况。因此，对微震信号和爆破震动信号的自动识别研究具有重要的现实意义[2-3]。

目前，使用较多的微震信号特征信息提取方法有两种，即多参数分析法和时频分析法。时频分析法主要包括小波变换(wavelet transform，简称WT)[4]、傅里叶变换(fourier transform，简称FT)[5]、小波包变换(wavelet packet decomposition，简称WPD)[6-7]、经验模态分解(empirical mode decomposition,简称EMD)[8]等方法。然而有些方法本身存在一定缺陷，会带来不准确的分析结果，如：傅里叶变换法不能很好地刻画信号的局部特征，只能做初步的识别；小波变换和小波包变换法会受到小波基和分解层次的限制。多参数分析法对微震信号的识别效果较好[9-10]，但其对采集信号的准确度有较高的要求，由于特征参数复杂，实现过程相对困难。

经验小波变换(empirical wavelet transform,简称EWT)在频谱上进行适当的分割，并在各个频带上建立小波滤波器组，从而将信号分解成多个频率特征信息相异的分量[11]。与EMD算法相比较，EWT算法具有良好的理论基础，并解决了EMD等算法出现的模态混叠问题，且计算量要远小于EMD算法。目前，EWT算法已经被广泛应用于各个领域，如医学领域[12]、故障诊断[13]等，但基于EWT算法的微震信号识别研究还鲜见报道。

基于此，尝试将EWT算法引入到微震信号分析领域。奇异值分解(singular value decomposition，简称SVD)能有效压缩矩阵数据，并精细描述信号序列本征属性，将其与时频分析算法进行组合能够得到不同的特征提取模型，如WPD-SVD[7]、EMD-SVD[8]等。EMD-SVD模型将分解出的模态分量作为矩阵的行向量，然后按频率高低依次排列构造复合矩阵，对矩阵进行SVD计算，算出的奇异值是从大到小排列的，但各个分量所对应的奇异值与分量的频率并不是一一对应的，容易使各个分量的特征信息丢失[14]。鉴于此，利用EWT算法分解得到多个分量，再利用互信息对分量进行筛选，进而分别对保留的分量构建Hankel矩阵，利用SVD计算Hankel，提取各个Hankel矩阵的奇异值平均值、方均根值、标准差作为模型识别的特征量，最后通过构建的支持向量机(support vector machine, 简称SVM)自动识别网络对微震和爆破信号进行准确识别，以期得到一种有效的微震信号识别方法。

1 经验小波变换

2013年，法国学者Gilles提出了经验小波变换，将模态看作调幅-调频(AM-FM)信号。针对AM-FM窄频带、高幅值的特征，EWT算法可实现显著模态的搜索及提取。其主要流程如下：

1)由于在截取记录时，样本长度选择不合适或者某些外界原因(如传感器的基础运动、零点漂移等造成的波形偏移)会导致趋势项的产生，因此通过最小二乘法对原始信号进行去趋势项处理[14];

2)通过傅里叶变换法计算输入信号的频谱，并归一化到[0,π]，设置模态个数M；

3)计算2个连续局部极大值之间的中间频率点，作为划分频谱的分界ωn(n=1,2，…，M-1)；

4)依据分割的频谱构建小波函数ψn(ω)和尺度函数φn(ω)[11]；

5)应用傅里叶反变换计算F(ω)×ψn(ω)和F(ω)×φn(ω)，从而可得到各个分量的时域表达式。

2 奇异值分解

原始信号经EWT变换后，将得到的各个分量(f1，f2，…，fJ)依尺度按行排列，构成矩阵M，然后利用SVD对矩阵M进行分解，将算出的奇异值作为识别的特征参数，这是最自然、最直接、应用最广泛的时频分析法与SVD组合的特征提取模型。但相关研究表明，除非已从分量信号中提取出了差异明显的特征信息，否则对矩阵M直接进行奇异值分解并不能对特征信息的提取效果起到较大的改进作用[15]。为了能更有效地利用SVD对微震信号进行特征提取，需要先对得到的各个分量分别进行处理。对每个分量分别构建Hankel矩阵Ha，可得下式：

(1)

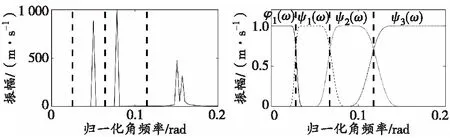
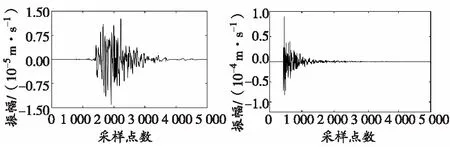
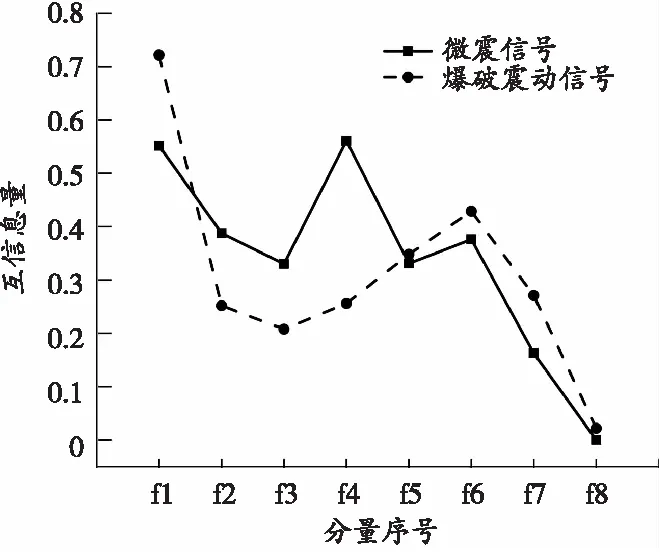
式中1≤a≤J，且1

特征矩阵Ha行列维数的选择应满足[16]：当N为偶数时，行数m=N/2+1；当N为奇数时，行数和列数均为m=n(N+1)/2。

对特征矩阵H进行奇异值分解，可得下式：

(2)

3 仿真信号研究

为了验证EWT有效分解信号的能力，构建仿真信号x(t)进行考查。仿真信号x(t)由调频信号、调幅信号和正弦信号组成，t∈[0,1]，并将分解结果与EMD法进行比较，仿真信号如下：

EWT的输出是由N-1个小波函数和1个尺度函数分别进行滤波的结果。EWT的频谱分割图及其小波滤波器组图如图1所示，仿真信号EMD、EWT的分解结果如图2、图3所示。

(a)频谱分割图 (b)小波滤波器组图

图2 仿真信号EMD分解结果

图3 仿真信号EWT分解结果

由图1可见，仿真信号EWT在频谱中计算出全部的极大值，将所有极大值按降序排列，根据前期假设的模态个数确定保留的极大值，以2个相邻极大值之间的中间频率点作为划分频谱的界限，再通过尺度函数和小波函数对仿真信号进行滤波。

由图2可以看出，imf1、imf2、imf3出现了模态混叠情况，另外得到了多个低频分量，这些分量原本属于同一主分量，但由于EMD算法采用不合理的终止条件，出现过分解，产生了虚假模态，这样既消耗计算时间又影响算法性能，而且虚假模态的产生会影响后期的特征提取。

由图3可知，通过EWT算法得到的分量f1～f3分别与原信号中50、25、16 Hz的分量相对应，且各个分量的吻合度和原始信号相比非常接近，不存在虚假分量。由此可见，EWT算法在提取微震信号特征时，具有明显优势。

4 工程实例研究

4.1 EWT分解

从漂塘钨矿微震监测系统数据中选取典型的爆破震动信号与微震信号进行对比分析。该矿安装的是南非IMS微震监测系统，传感器的采样频率为 6 000 Hz。通过对采集到的微震信号和爆破震动信号波形进行对比分析可知：微震信号持续时间相对较长，衰减较缓慢；爆破震动信号的持续时间较短，衰减较快，并且爆破震动信号的幅值要大于微震信号的幅值。这些分析结果通常是人工识别微震信号的一个依据，但地下地质条件复杂，接收到的信号不一定都存在这种差异，因此需要通过特征提取的方式对 2种信号进行量化。矿区监测到的岩体微震和爆破震动信号波形如图4所示。

(a)微震信号波形 (b)爆破震动信号波形

对微震信号和爆破震动信号进行EWT分解，微震信号得到7个分量，爆破震动信号得到8个分量，如图5所示。

(a)岩体微震

为了能更有效地提取信号特征，需要利用互信息量(MI，用符号IMI表示)对得到的分量进行筛选。IMI描述2个变量间存在共同信息量的多少，IMI越大则变量间的共同信息越多，相关性越强[18]。对于信号的第i个分量ci(t)与原始信号x(t)，二者之间的IMI定义为：

(3)

式中：p(ci)和p(x)分别是ci(t)与x(t)的边缘概率分布；p(ci，x)是ci(t)与x(t)的联合概率分布。

依据公式(3)计算各个分量与原始信号的互信息量。刘长良等[18]认为，当分量与原始信号的互信息量小于0.02时，可将该分量作为虚假分量进行剔除，所以选取图5(a)中前7个分量作为特征分量。各分量与原始信号的互信息量如图6所示。

图6 各分量与原始信号的互信息量

4.2 特征提取

利用筛选的主分量f1～f7分别构建Hankel矩阵Ha(a=1,2,…,7)，并对各个Hankel矩阵进行奇异值分解(SVD)，从而得到7组不同奇异值σ1,σ2,…,σr，每组奇异值σ1,σ2,…,σr由矩阵Ha唯一确定。由SVD性质可知，矩阵Ha这些非零奇异值σ1,σ2,…,σr反映的是矩阵的特征，由这些非零矩阵组成的特征向量σ=(σ1,σ2,…,σr)唯一表征了微震信号的特征。为突显微震信号和爆破震动信号的差异，对特征向量σ进行分析，计算平均值h1、方均根值h2及标准差h3，并作为微震信号的特征参数。h1、h2、h3表达式如下：

(4)

(5)

(6)

根据微震信号和爆破震动信号各个分量的特征参数h1、h2、h3的数值变化，探讨特征参数h1、h2、h3是否能有效地区分微震与爆破震动信号。由式(1)构建Hankel矩阵，并对Hankel矩阵进行奇异值分解，然后通过式(4)～(6)得到各个分量的奇异值平均值h1、方均根值h2、标准差h3。各分量Hankel矩阵的平均值、方均根值、标准差变化如图7所示。

(a)平均值

由图7(a)可看出，爆破震动信号前6个分量的奇异值平均值均大于微震信号前6个分量的奇异值平均值，其中前3个分量的奇异值平均值差异较大；而第6个分量的奇异值平均值近似相等，爆破震动信号第7个分量的奇异值平均值要小于微震信号的奇异值平均值。

由图7(b)、(c)可看出，爆破震动信号各分量Hankel矩阵的方均根值和标准差都要大于微震信号的方均根值和标准差，且前5个分量的差异性较大；爆破震动信号与微震信号第6个分量的方均根值近似相等。

由图7可知，岩体微震信号和爆破震动信号各个分量的奇异值平均值、方均根值、标准差均存在一定的差异，且前5个分量差异较大，所以，利用各个分量的奇异值平均值、方均根值、标准差作为微震信号识别的特征量是可行的。然而，上述过程只是对特征参数的定性分析，未对微震信号做定量识别。鉴于此，笔者借助机器学习方法进一步挖掘数据的内在信息，利用模式识别方法对微震信号进行识别分类。

4.3 SVM分类识别

SVM是在结构风险最小化的基础上构建的机器学习方法，其克服了小样本学习和局部极大值的问题，并在泛化能力和学习精度间进行了较好的权衡。近年来，有学者将SVM应用于地震震相识别[20]、岩爆预测[21]等方面，并取得了不少研究成果。笔者选择SVM分类器作为微震信号辨识的分类器，利用微震信号和爆破震动信号各分量的奇异值平均值、方均根值、标准差作为特征量，建立基于SVM的微震信号自动识别体系。

1)从已有数据中随机选取岩体微震和爆破震动信号各200组，利用上述方法得到微震信号和爆破震动信号前7个分量的奇异值平均值、方均根值、标准差，并将此作为特征量；将前100组作为训练样本数据，后100组作为测试样本数据。将岩体微震信号的类别设定为1，爆破震动信号的类别设定为2。

2)分类器参数选择：选用RBF (radial basis function，简称RBF)径向基核函数ψ(xi,xj)=e-γ‖xi-xj‖2,其中γ>0,惩罚参数C=2,核函数参数γ=1。

依据构建的SVM微震信号自动识别体系，对微震信号和爆破震动信号进行识别，为了测试本方法特征提取的有效性，与目前应用最广泛的奇异值分解法进行比较。该方法是将EWT分解得到的7个分量构建成复合矩阵，并直接对复合矩阵进行SVD处理，将得到的奇异值作为特征量进行识别，两种特征提取方法的识别效果如表1所示。

表1 两种特征提取方法识别效果对比

由表1可知，采用EWT_Hankel和SVD提取微震和爆破震动信号各个分量的奇异值平均值、方均根值、标准差作为特征量，可以较好地实现两种信号的识别，且准确率达到92.5%；采用EWT和SVD提取微震和爆破震动信号奇异值作为特征量，对微震信号的识别准确率较低，仅为83.5%。所以基于EWT_Hankel_SVD和SVM构建的微震信号自动识别模型，可以有效地识别爆破震动信号和微震信号。这为获取矿山信号特征、研究矿山信号分类提供了一种新思路和新方法。

5 结论

1)经验小波变换是一种非线性、非平稳信号的分析处理工具，其结合了小波变换和EMD算法的优点，具有充分的理论基础和自适应性。仿真信号结果表明，EWT算法能够有效地解决模态混叠问题，从而更加准确地分解信号，特别适用于处理微震信号类的非平稳信号。

2)时频分析法和SVD组合的模式应用最广泛，该模式通常是将时频分析得到的各个主分量构建成复合矩阵，并直接对矩阵进行SVD处理；笔者将得到的各个主分量分别构建Hankel矩阵，之后通过SVD计算每个Hankel矩阵的奇异值，将各个Hankel矩阵奇异值平均值、方均根值、标准差这3个值作为模式识别的特征量，显著提高了微震信号识别率。

3)通过EWT_Hankel_SVD和SVM网络构建的微震信号自动识别模型分类识别准确率达到92.5%；应用最广泛的奇异值分解特征提取法识别准确率为83.5%。表明基于EWT_Hankel_SVD的特征提取方法是有效的，且具有较高的准确率。该方法为研究矿山信号、获取矿山信号特征提供了一种新思路和新方法。