基于综合指标的最优冗余陀螺配置确定方法
2020-09-09冯佳佳王佐伟
冯佳佳, 王佐伟
(1.北京控制工程研究所,北京100190;2.空间智能控制技术重点实验室,北京100190)
0 引言
陀螺(惯性姿态敏感器)是航天器高精度、高稳定度控制系统中关键的姿态敏感器,陀螺配置主要指陀螺的类型、安装数目、安装结构、冗余备份方式等。由于航天器的姿态性能指标(姿态确定精度、指向精度、姿态稳定度)均与参与闭环的陀螺配置相关,因此陀螺的配置对航天器控制系统的设计来说至关重要[1]。
目前,陀螺配置主要采取冗余措施[2],且有一定的研究成果。文献[3]、文献[4]以可靠性为基础对陀螺的冗余配置进行了研究,通过判别可靠性确定出了陀螺冗余配置的最佳安装数目;文献[5]~文献[8]分别以导航特性、故障诊断性和测量精度为基础对陀螺的冗余配置进行了研究,通过优化陀螺的冗余配置结构使得系统获得了在某一方面的最优特性;文献[9]~文献[11]分别以可靠性、精度、故障诊断性等指标为基础对陀螺的冗余配置进行对比研究,通过指标对比确定出了陀螺在某些性能方面的最优配置结构。然而,目前的研究均针对几种固定构型的陀螺冗余配置,以单项指标或多项指标为基础进行对比分析,没有形成系统性、理论性的确定最优冗余陀螺配置的方法。事实上,在实际的工程中,陀螺在进行配置时应系统性的考虑陀螺冗余配置的形式,并综合考查可靠性、精度、质量、成本等综合指标,这样才能确定出最优的冗余配置。因此,以综合指标为基础对陀螺的冗余配置进行系统性的研究十分有必要。
本文首先以工程中普遍采用的陀螺均匀斜置式为对象,系统性给出陀螺斜置式的安装结构,并以测量误差最小为目标确定出确定数目的最优陀螺冗余安装结构,然后对陀螺冗余配置的综合指标进行详细的分析,最后利用优化评价方法对不同数目的陀螺冗余配置进行综合评价,从而确定出陀螺斜置式安装的最优配置,从理论上给出了最优冗余陀螺配置的确定方法。需要说明的是,本文所研究的陀螺均为同一类型。
1 陀螺斜置式最优安装结构的确定
陀螺在进行配置时,首先需要确定陀螺的最优安装结构。由文献[12]可知,目前工程上普遍采用斜置式安装结构,即将n个陀螺的测量轴沿半锥顶角为β的锥面均匀分布安装,该安装结构一方面便于进行规范化的测量转换以及故障诊断、隔离和重构 (Fault Detection,Isolation and Reconfiguration,FDIR)设计,另一方面工程上也易于实现。图1给出了4个陀螺的斜置式安装结构。

图1 4个陀螺的斜置式安装结构Fig.1 Inclined installation structure for four gyroscopes
由安装结构可以得到n个陀螺的斜置式安装矩阵H

式(1)中,α为初始安装角,工程上一般取为 0°。
在冗余配置的系统中,冗余陀螺的输出方程为

式(2)中,X∈R3为待测的状态(通常为三轴角速度),Z∈Rn为n个陀螺的量测值(n≥3),H为陀螺的安装矩阵,ε为零均值的Gauss白噪声。
由文献[13]可知,Harrison和Gai提出如下性能指标

当安装矩阵H使得Fp取得最小值,则系统由噪声所引起的误差最小,系统可获得最佳的特性。
因此,对于n个陀螺的斜置安装结构,当半锥安装顶角为
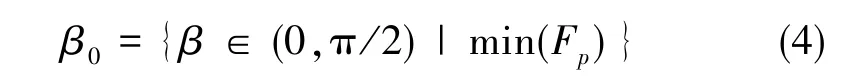
此时的安装结构为n个陀螺的斜置式最优安装结构。
在陀螺安装数目已经确定的情况下,该安装结构为最优冗余配置,但在陀螺的安装数目不确定的情况下,陀螺的最优冗余配置还不能确定。事实上,随着陀螺数目的增加,系统的可靠性和精度都随着增加,但相应的成本代价等指标也会相应的增加。
因此,下一步将确定出斜置式陀螺的最优冗余安装数目。
2 陀螺斜置式最优安装数目的确定
2.1 综合指标
在陀螺最优安装数目确定之前,首先需要确定出工程中陀螺配置的综合性能指标。
结合工程实际经验,对航天器控制系统设计中陀螺冗余配置进行详细系统的分析,陀螺配置的综合指标如图2所示。
其各项指标的含义及计算公式为:
(1)基本可靠性
基本可靠性是指在规定条件下及规定时间内的无故障工作能力,它反映的是对维修资源的需求[14]。在陀螺的冗余配置中,它与陀螺的工作状态以及故障诊断与隔离等都密切相关。因此,在实际工程中,一般要求基本可靠性越高越好。在n个陀螺的冗余配置中,基本可靠性为
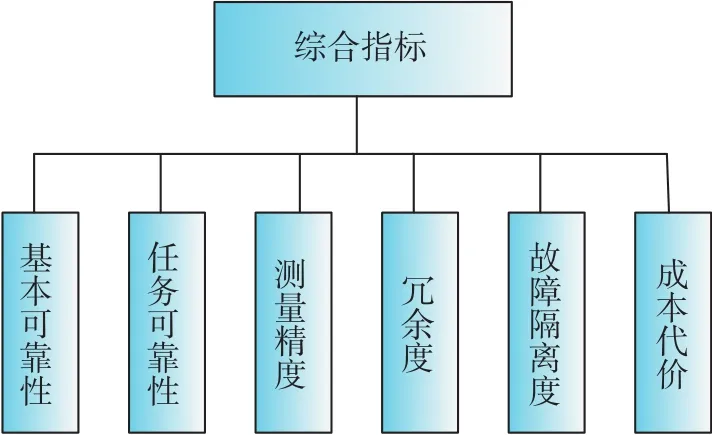
图2 陀螺配置的综合指标Fig.2 Comprehensive index of gyroscope configuration

式(5)中,R0为单个陀螺的可靠性。
(2)任务可靠性
任务可靠性是指在规定的任务剖面内完成规定功能的能力,它反映的是对任务成功性的要求[14]。在实际的工程中,任务成功性是首要和主要追求的目标,一般要求任务成功性越高越好。在陀螺斜置式冗余配置中,由于任意3个陀螺均不共面,故只要有任意3个陀螺无故障就可以保证任务的成功,所以任务可靠性为
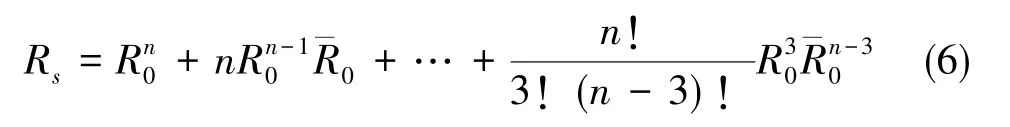
(3)测量精度
冗余陀螺的测量方程是一个含有随机误差的代数方程,一般情况将测量得到的冗余数据运用最小二乘估计进行处理。根据最小二乘估计原理,要求估计值能使所有测量值相对估计值的偏差平方和为最小。当所有冗余陀螺都正常工作时,满足最小二乘判据的最佳值为
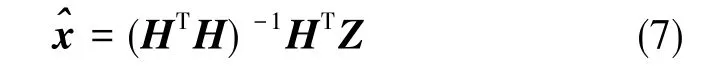
当陀螺采用无冗余正交安装时,陀螺测量单元的3个轴向的测量精度就是陀螺的测量精度。当采用冗余配置后,陀螺测量单元的测量精度有无提高不能确定,需要引入指标函数来确定。由文献[13]可知,可以采用如下的测量精度指标函数
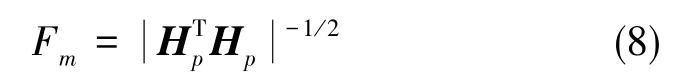
式(8)中,Hp为确定安装陀螺数目下的最优安装矩阵,可由式(1)~式(4)计算得到。Fm的数值越小,则测量精度越高。
(4)冗余度
冗余度是指陀螺的冗余程度,它反映的是系

式(10)中, [·]的含义为取整计算。
(6)成本代价
成本代价是指陀螺冗余配置时所付出的所有代价,这里的代价是广义的,它可以是价格、重量、体积、功耗、安装难度、维护管理等,也可以是以上诸多因素的综合[19]。因此,对于n个陀螺的冗余配置来说,成本代价可以定义为

成本代价函数与安装的陀螺个数成指数函数关系,一般可根据工程实际进行确定。
2.2 优化评价方法
在综合指标确定后,下一步将确定出评价方法。目前的评价方法主要有两类,一类为主观评价方法,另一类为客观评价方法。这两类评价方法各有优缺点,为了让评价结果更加科学合理,同时又兼顾评估专家对指标的青睐,尽量减少主观随意性,故采用优化评价方法[20]。优化评价方法以最小二乘为工具对主观评价方法和客观评价方法进行优化,以各方案对正负理想方案的贴近度为依据从而确定出方案的优劣。
(1)指标数值归一化
由于综合指标中的量纲各不相同,需要进行统工作模式的备份数[15]。n个陀螺中只要有3个无故障,便可保证系统正常可靠地工作。因此,根据文献[15],冗余度可定义为

(5)故障隔离度
故障隔离度是指当系统中的陀螺出现故障后能有效进行隔离的程度。从故障诊断与隔离的角度来分析,在3维空间中,当陀螺的冗余配置数为4时,只能检测出故障而不能隔离出故障陀螺;若使系统具有隔离P个单故障陀螺的能力,则至少需要(P+3+1)个陀螺。当其中1个陀螺发生故障时,在其没有完全被隔离的情况下另1个陀螺也发生了相似的故障,则不能按上述的方法进行配置。当K个陀螺同时发生故障时,如果系统具有故障检测与故障隔离的能力,则至少需要有(2K+3)个陀螺[16-18]。本文主要考虑能被隔离出同时发生故障的陀螺数,从这个角度可以定义故障隔离度为规范化处理[21]。
设有a个评价对象及b个评价指标,以xij表示第i个待评对象的第j个评价指标值,构成矩阵为X=(xij)a×b, 将其转换成规范化矩阵R=(rij)a×b。 其中,对越小越优性指标采用如下转换形式

对越大越优性指标采用如下转换形式
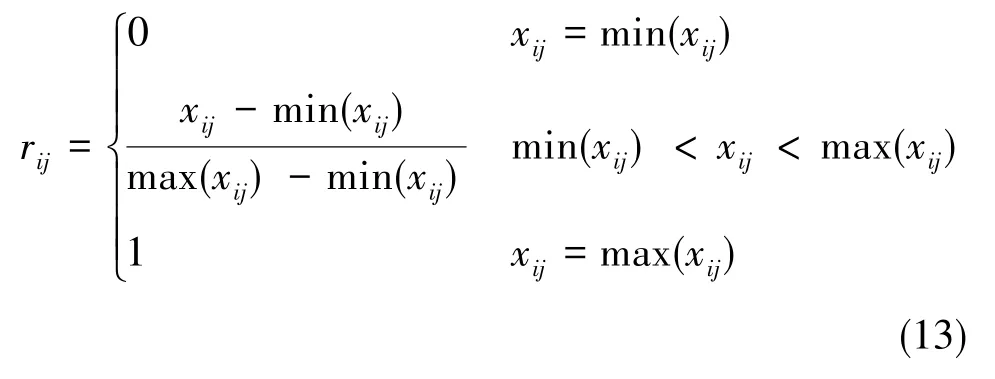
(2)安装数目的确定
在a个评价对象及b个评价指标中,设主观评价方法给出的指标权重为U=[u1u2…ub]T,客观评价方法给出的指标权重为V=[v1v2…vb]T,各指标优化组合权重为W=[w1w2…wb]T。
第i个评价对象的评价值为

对评价指标而言,主客观评价值的偏差越小越好。因此,建立最小二乘模型[22]

对式(15)作Lagrange函数,可得
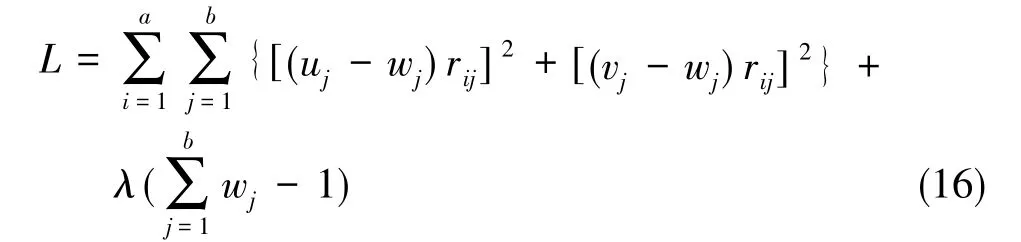
令

式(17)、 式(18)用矩阵可表示为

由式(19)可得

将规范化矩阵R按列单位化,则得到单位化矩阵Z=(zij)a×b。
取各指标的最大值构成正理想方案,即
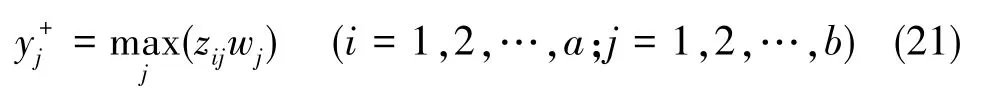
取各指标的最小值构成负理想方案,即

定义

式(23)、 式(24)中,Li、Di分别为方案Ai(i=1,2,…,a)对正理想方案A+和负理想方案A-的贴近度。
评价系数Fi定义为
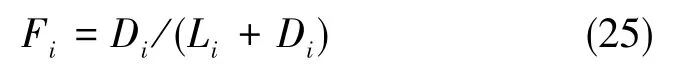
通过评价系数Fi对不同陀螺的安装数目进行评价,Fi的数值越大,则冗余陀螺配置越优,从而可以确定出最优的冗余陀螺安装数目,即最优的冗余陀螺配置。
3 陀螺斜置式的分析与计算
为了寻得最优的冗余陀螺配置,需要综合评价出n≥4时的斜置式陀螺冗余配置情况。对于由斜置式陀螺冗余配置组成的系统,当n无限增大时,会大大增加系统的体积、质量、成本和控制复杂度,这不利于实际应用,所以本文只考虑n∈[4,15]的情况。表1给出了n取不同值时各项指标的情况。
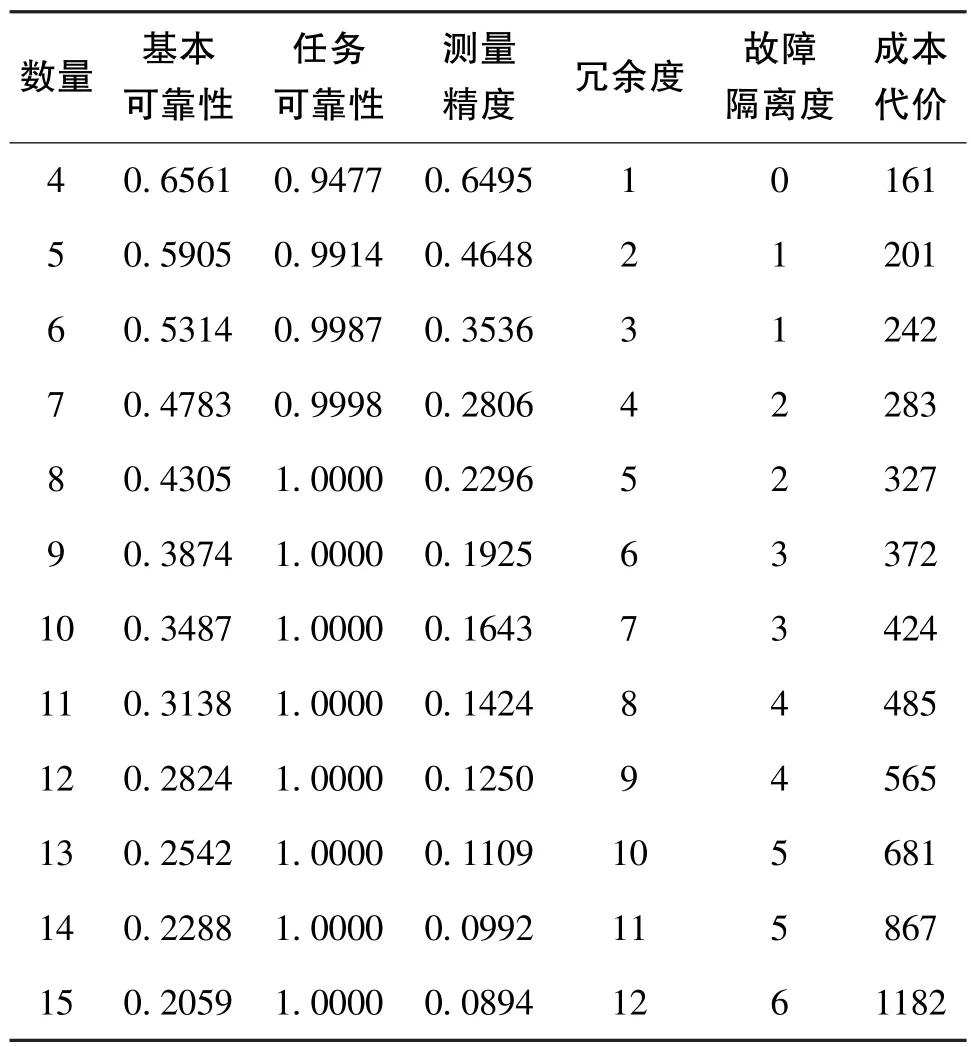
表1 n变化时的各项指标Table 1 Index values when n changes
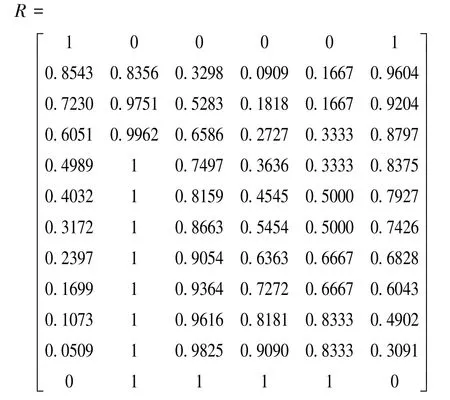
由于基本可靠性、任务可靠性、冗余度、故障隔离度都为越大越优型指标,测量精度、成本代价为越小越优型指标,则将指标进行规范化可得
采用层次分析(Analytic Hierarchy Process,AHP)方法[23]确定的主观权重U为

采用熵方法[21]确定的客观权重V为

通过式(20)计算得到的优化权重W为

最后, 利用式(21)~式(25)得到的计算结果如表2所示。

表2 计算结果Table 2 Calculation results
由表2可知,n=7时的F数值最大,即当陀螺的安装数目为7时的冗余配置为陀螺斜置式的最优冗余配置。
事实上,一方面随着陀螺安装数目的增加,任务可靠性、测量精度等也会增加,不过随着数目增加到一定程度,它们增加的幅值不是很明显,但是基本可靠性会显著降低,成本代价会显著增加,故陀螺安装数目不能取较大值;另一方面本文引入了故障隔离度这一指标,对于陀螺安装数目较小时,不能有效的隔离故障,而且任务可靠性、测量精度等也会很低,从这个角度来说,7个陀螺的斜置安装为最优冗余配置,该结论对工程实际应用具有指导作用。
需要说明的是:1)目前在航天器实际工程中,陀螺的冗余配置数量一般根据航天任务的可靠性指标进行确定,较少考虑其他指标因素,本文的研究可以作为在满足航天任务可靠性的前提下确定最优冗余陀螺配置的方法。2)综合指标包括很多因素,有些因素可能还引入主观因素在里面,如成本代价。此外,单个陀螺的基本可靠性需要有足够的样本支撑,基本可靠性选取的不同会影响最终结果。3)工程上为了陀螺故障定位(短期时间内仅考虑单陀螺故障,一般不考虑多陀螺故障)一般会开启5个陀螺,且用于测量的陀螺数目可能为3~5个,所以文中无论是理论分析的精度指标还是任务可靠性指标均与实际应用有所差别。因此,本文的理论研究均是在一定的前提下实现的,对工程具有理论指导意义,但不能完全等同于工程。
4 结论
本文提出了一种确定最优冗余陀螺配置的方法,该方法综合考虑了陀螺配置的各项综合性能指标,并利用该方法对斜置式陀螺冗余配置进行了分析和计算。结果表明,当陀螺的安装数目为7时为最优冗余配置,该结论对工程实际具有指导作用。同时,本文所提出的方法也可以用于不同陀螺构型冗余配置的对比分析,为陀螺的冗余配置提供系统性的理论方法和依据。
