基于速度交流的共生多种群粒子群算法

赵志彪， 李 瑞， 刘 彬， 周武洲

(1. 天津职业技术师范大学自动化与电气工程学院，天津300222；2. 燕山大学电气工程学院，河北秦皇岛066004)

1 引 言

粒子群算法是优化领域一种典型的群体智能寻优算法，受到达尔文进化论和自然现象的启发，模仿鸟群的群体行为对目标进行优化搜索，理论结构简单且参数较少，具有鲁棒性强、搜索效率高的特点，已经广泛应用于工程实践和函数优化等领域[1～7]。但是传统的粒子群算法存在易陷入局部最优、求解精度不高等缺陷。因此，近年来不少学者对粒子群算法进行了大量研究。

针对单种群粒子群算法，赵鹏程等提出了一种带随机扰动的混沌粒子群算法，算法采用混沌映射保持种群的多样性，当粒子出现“聚集”现象时加入随机扰动策略，在求解高维复杂优化问题时取得了较好的求解精度[8,9]；Liang等提出了采用分维度综合学习策略的粒子群算法，算法在维持种群多样性的同时未增加计算复杂度，具有较好的全局搜索能力[10]；陶新民等提出了改进的粒子群与K均值算法混合的聚类算法，通过两种算法的有机结合，有效实现了算法全局搜索能力及收敛速度的平衡[11]。

目前的这些单种群算法虽然一定程度上提高了粒子群算法的性能，但算法执行单一种群的操作模式，每个粒子都趋向于同一种群的“社会部分”，导致解的多样性较低，种群中的粒子聚集到一起很难摆脱局部最优状态，并不能弥补算法的缺陷[12]。因此，多种群的构建逐渐成为提升算法寻优效率的研究热点。Liang等提出了一种动态的多种群粒子群算法，将整个种群划分为若干个小种群，并周期性地随机重组小种群，在多峰问题上表现出良好的搜索能力[12]；刘衍民等提出了一种基于K-均值聚类的多种群粒子群算法，根据聚类中心对小种群进行动态划分，提高了种群的多样性[13]；高云龙等提出了一种基于多种群粒子群算法和布谷鸟搜索的联合寻优算法，算法采用中位数聚类将整个种群动态划分为若干个小种群，并将每个小种群的最优粒子作为高层种群的粒子进行深度优化，提高了算法的全局搜索能力[14]； Bergh F V D等提出了一种利用多个子种群分别优化解向量各维度的多种群粒子群算法，避免了“two steps forward，one step back”的现象[15]；Niu B等提出了一种基于互利共生和共栖思想的主从式结构的多群体协同进化粒子群算法，该结构有效地保证了算法开发与探测能力的平衡[16]。上述算法的多种群策略都是基于粒子之间的位置信息共享，并没有考虑粒子的速度信息。 Zhang J等提出了一种自适应多种群协同粒子群算法，子种群间通过分享速度和位置信息实现算法的全局搜索，具有较好的求解高维优化问题的能力[17]。

受上述多种群粒子群算法的启发，本文提出了一种基于速度交流的共生多种群粒子群算法(symbiosis multi-population particle swarm optimization algorithm based on velocity communication，SMPSO)。SMPSO算法中，构建具有共生关系的主从群结构，在提升算法解集多样性的同时平衡局部与全局搜索能力。根据从种群间的速度信息交流机制进行子种群的划分，即以固定种群动态交流速度信息的方式对子种群进行规划，有效实现子种群搜索领域的分割，从而增强算法的探索与开发能力。当算法陷入局部最优时，引入自适应变异策略对主种群个体进行变异，提升SMPSO算法跳出局部最优的能力。在仿真实验中，对不同函数寻优测试，均显示出该算法优良的搜索能力和寻优性能。

2 SMPSO算法研究

2.1 多种群算法构建

传统粒子群算法采用单一种群的模式，在处理复杂的优化问题时，具有易陷入局部最优、求解精度不高的缺点；而多种群粒子群算法的运行效率和求解精度往往优于单种群粒子群算法[18]。因此，本文构建了基于速度交流的共生多种群粒子群算法(SMPSO)，算法的优化框架如图1所示。

图1 算法优化框架Fig.1 Algorithm optimization framework

本文将SMPSO分割为主种群和从种群两部分。其中，从种群采用速度交流机制，被划分为4个子种群p1,p2,p3,p4，负责在解空间中全局广度搜索，主种群根据自适应变异策略负责在解空间中局部精度搜索。搜索过程中，从种群将获得的最优信息Plocal-best分享给主种群，而主种群根据共生群体(从种群)的经验以及自身经验获得整个种群的最优状态Pglobal-best再反馈给从种群，从而建立主从群间的共生结构。这种结构能够实现主从种群间的互利共生，在一定程度上避免了个体信息误判造成的陷入局部最优的危险。

从种群中4个子种群p1,p2,p3,p4速度交流机制的思想是：一次迭代过程中，采用不同惯性权值与学习因子参数组合的子种群p1和p2作为基本子种群，将速度信息分享给子种群p3，从而影响子种群p3的搜索行为；子种群p1,p2,p3再将速度信息分享给子种群p4，用于影响子种群p4的搜索行为。该操作使4个子种群粒子的搜索性能具有差异性，使解空间被划为4个子种群对应独立的子空间，实现优化问题搜索领域的有效规划，既满足子种群间的自由竞争，又可以实现子种群间的信息交流。本节将详细描述从种群中4个子种群p1,p2,p3,p4的更新方式。

(1)

(2)

为了产生不同于p1,p2的粒子搜索轨迹，子种群p3的速度受子种群p1,p2的引导，通过对子种群p1,p2速度信息的记忆，自适应更新其速度，子种群p3的粒子速度迭代如式(3)所示。

(3)

式中：w3表示子种群p3的惯性权重；c31表示子种群p3的自我学习因子；c32表示子种群p3的社会学习因子；s1,s2为子种群p3的影响因子。

利用式(4)和式(5)对s1和s2进行计算。

s1=(V1+V2)/V1

(4)

s2=(V1+V2)/V2

(5)

式中：V1为子种群p1的个体适应度值(本文为目标函数值)；V2为子种群p2的个体适应度值。

s1、s2决定子种群p1、p2对子种群p3的影响程度。sG(G=1,2)越大，子种群pG(G=1,2)对子种群p3的影响程度越大。

综上，子种群p1,p2,p3在解空间中占有不同的搜索领域。为了使解空间得到更全面的探索，本文建立了相异于子种群p1,p2,p3搜索方向的子种群p4。子种群p4用于搜索被子种群p1,p2,p3忽略的解空间，从而使从种群的全局搜索性能更完善。子种群p4的速度受其它3个子种群的引导，通过对子种群p1,p2,p3速度信息的记忆，自适应更新其自身的速度。子种群p4的更新如式(6)所示。

(6)

在速度迭代更新的基础上，子种群p1、p2、p3对位置进行相应的更新，子种群p1、p2、p3的粒子位置更新如式(7)所示。

(7)

子种群p4的速度接收子种群p1,p2,p3的速度信息，决定其粒子移动的方向和距离，而全局最优状态Pglobal-best可以引导种群寻找最优解。因此为了增强子种群p4的搜索能力，利用式(8)对p4粒子位置迭代更新。

(8)

式中：α1,α2,α3为影响因子。

α1,α2,α3分别决定式(8)各元素对子种群p4搜索能力的影响程度，且满足α1+α2+α3=1。αr(r=1,2,3)越大，对子种群p4的影响程度越大，分别设定α1,α2,α3为1/6,1/3,1/2[17]。

从种群每次完成迭代，利用式(9)对子种群p1，p2，p3，p4的最优位置Plocal-best-G(G=1,2,3,4)进行筛选，从PLocal-best-G(G=1,2,3,4)中选择最优位置状态Plocal-best，将Plocal-best分享给主种群。

Plocal-best=min{Plocal-best-G,G=1,2,3,4}

(9)

主种群综合自身最好经验和从种群最好经验Plocal-best，进行状态的更新，获得整个种群的最优状态Pglobal-best,并将Pglobal-best再次反馈给从种群,作为从种群的社会部分，从而实现主种群与从种群的互利共生。

主种群的粒子个数为M，第i个粒子的位置表示为[xi1,xi2,xi3,…xiD]，第i个粒子的速度表示为[vi1,vi2,vi3,…viD]，利用式(10)对主种群的粒子速度迭代更新。

vij(t+1)=wvij(t)+c1r1(Pij(t)-xij(t))+
λ1c2r2(Pglobal-best(t)-xij(t))+
λ2c3r3(Plocal-best(t)-xij(t))

(10)

式中：w为主种群的惯性权值；c1为主种群的自我学习因子；c2、c3为主种群社会学习因子；r1、r2、r3为[0,1]间的随机数；λ1,λ2为主种群的影响因子。

λ1,λ2分别决定Pglobal-best,Plocal-best对主种群搜索行为的影响程度，且满足λ1+λ2=1。λ1,λ2根据式(11)和式(12)进行计算。

λ1=1-VG/(VG+VL)

(11)

λ2=1-VL/(VG+VL)

(12)

式中：VG为Pglobal-best对应的个体适应度值；VL为Plocal-best对应的个体适应度值。

公式(13)为主种群的粒子位置更新公式:

xij(t+1)=xij(t)+vij(t+1)

(13)

通过分析上述算法运行结构可知，从种群采用速度交流机制被划分为4个子种群p1，p2，p3，p4。子种群p1，p2作为从种群的基本子种群，分别传递速度信息给子种群p3和p4。不仅实现子种群粒子速度的自适应更新与子区域的合理规划，提高从种群的全局探索与开发能力；而且将全局搜索的最优状态Plocal-best发送给主种群，协助主种群有效的进行局部搜索。主种群综合从种群的全局最优位置进行局部深度寻优，获得整个种群的最优位置Pglobal-best反馈给从种群，引导4个子种群向全局最优解逼近，从而建立了具有共生关系的主从群结构。多种群策略提升了算法解集多样性,主从群结构充分利用了粒子群算法的局部搜索能力，实现各种群间的速度与位置信息共享。因此，本文所建立的主从群共生关系为算法的优化提供了优良的搜索环境。

2.2 自适应变异策略

在进化策略中引入柯西分布的变异算子可以降低算法陷入局部最优的机会[19]。为了进一步提高算法的搜索能力，本文将柯西变异算子引入主种群算法中，从而提高算法跳出局部最优的能力。

在算法的初始阶段，主要运行多种群的算法结构。当算法连续2次迭代找到的最优值在0.01%内变化，则认为算法本次迭代陷入局部最优。此时根据适应度值对主种群的粒子从小到大进行排序，引入柯西变异算子对主种群排名在后50%的粒子进行变异，从而引导算法跳出局部最优。自适应变异策略的规则为：

xij-new=xij+Δxij·φ·rand

(14)

(15)

式中：φ为尺度压缩因子，取值范围为[0,0.1]；Δxij为变量的柯西算子变异增量；rand表示(0,1)范围内的随机数。

经过自适应变异的新个体将取代旧个体，继续进行算法迭代。

2.3 SMPSO算法参数设置策略

粒子群算法的惯性权值和学习因子的选取对算法的优化性能有很大的影响，不同的参数组合下，粒子的轨迹形式是不同的，参数组合决定了粒子搜索能力的大小[20]。综合考虑各种群的搜索性能和影响因素，本文对主从群分别选取了合适的惯性权值与学习因子的参数组合，提高种群多样性的同时增强算法的搜索能力。

子种群p1的惯性权值w1=0.4,学习因子c11=2，c12=2； 子种群p2的惯性权值w2=0.75,学习因子如式(16)和式(17)所示[20]。

(16)

(17)

子种群p3的搜索性能受子种群p1，p2的综合影响。考虑到子种群p1，p2的动态迭代效应，子种群p3的惯性权值与学习因子采用固定数值的设置方法，具体设定通过下文实验获得，此处不再赘述。子种群p4没有相应的惯性权值和学习因子参数，搜索行为受到子种群p1，p2，p3的综合影响。

主种群在整个算法结构中具有深度局部优化作用。综合考虑主种群对算法搜索性能的影响，惯性权值w采用双指数函数的设置形式[21]，如式(18)。

w=exp(-exp(-(T-t)/T))

(18)

双指数函数是一个单调递减的非线性函数，因此惯性权值w随着迭代次数t增加而减小；从而在算法迭代初期，主种群具有较大的迭代步长，加快其搜索速度。随着算法逐渐逼近最优解，主种群的惯性权值不断衰减，主种群粒子的步长也不断减小，使主种群在最优解附近进行有效的小范围搜索。通过下文实验对主种群的学习因子进行取值分析。

2.4 SMPSO算法整体流程

在粒子群算法中，速度和社会影响因素在算法中的作用是举足轻重的。在一次飞行中，种群根据当前种群最优点不一定找到最优的搜索领域，因此每个种群应该更多的关注其它群体中的个体与社会信息。本文的策略是粒子在飞行过程中综合其它种群中的粒子速度和位置最优信息进行寻优，建立具有共生关系的主从群结构；采用速度交流机制对从种群进行划分与联系，从全局与局部着手，建立了新颖的多种群粒子群算法；采用自适应变异策略与合适的参数组合进一步提升算法的搜索特性。SMPSO算法的流程如图2所示。

通过上述的算法分析与流程图的建立，所提出的改进算法的步骤总结如下：

Step1:设置算法参数：种群规模M，最大函数迭代次数T，学习因子c1和c2等；

Step2:初始化各种群的速度和位置；

Step3:利用式(1)～式(8)对从种群迭代更新，计算各子种群中粒子的适应度值，得到各子种群局部最优位置Plocal-best-G(G=1,2,3,4)，从中选择最优的位置Plocal-best；

Step4: 将从种群得到的Plocal-best发送给主种群，主群综合自身最好经验和从种群最好经验，利用式(10)～式(13)进行迭代更新，得到Pglobal-best；

Step5: 判断算法是否满足结束条件(最大迭代次数T)，如果满足，跳转到Step9，如果不满足，执行Step6；

Step6: 根据Pglobal-best的更新情况，判断算法是否陷入局部最优，如果算法陷入局部最优，执行Step7，否则执行Step8；

Step7： 利用式(14)和式(15)对主种群排在后50%的个体变异，并执行Step8；

Step8: 将主群的Pglobal-best发送给从种群，接着跳到Step3；

Step9： 输出Pglobal-best，即优化问题的解向量。

3 数值实验与结果分析

为了验证SMPSO算法的寻优性能和求解效率，本文选取5个基准测试函数进行SMPSO算法的性能测试，分别为: Sphere, Ackley, Griewank, Rastrigin, Schwefel。各测试函数具体属性如表1所示。

图2 SMPSO算法流程图Fig.2 SMPSO algorithm flowchart

表1 基准测试函数Tab.1 Benchmark function

本文进行了3组测试实验：(a)子种群p3的参数w3、c31和c32的取值分析；(b)主种群参数c1、c2和c3的取值分析；(c)与其它改进PSO算法的性能对比。为验证本文算法在不同的变量维度下的适用性，分别在10和30维的变量维数下进行(a), (b)和(c)的实验。为了避免算法运行的随机性，以上所有实验均独立运行30次，最大函数迭代次数T均为1 000，粒子个数统一设置为50。算法的评价指标为迭代得到的最优解与真实的全局最优解的适应度值之差，称为求解精度(AC)，其计算方法如式(19)所示。

AC=|f(Pglobal-best)-f(xopt)|

(19)

式中：Pglobal-best表示算法迭代得到的最优解；xopt表示真实的全局最优解；f表示目标函数。

3.1 参数w3,c31和c32的取值分析

由于在子种群p3中引入了3个需要预先设定的参数，即参数组合w3、c31和c32； 因此需要对3个参数进行取值分析。设置子种群p3的自我学习因子c31=2，社会学因子c32=2[22,23]，并对惯性权值w3选取了7个不同数值。

表2给出了在w3取值不同的情况下，算法对10维和30维的5个函数的30次测试的最优结果，其中每个函数最好的结果用黑体字标出。

表2 子种群p3中w3取值不同的优化结果Tab.2 Optimization result along with difference of w3 in subpopulation p3

从优化结果来看，对于10维和30维的Griewank，Ackley，Schwefel函数，在w3=0.5时SMPSO算法的最优结果均优于其它情况，表明w3=0.5为子种群p3惯性权值的最佳选择。在实际应用中，建议w3在[0,1]取值。本文的实验中，w3取0.5。

3.2 参数c1,c2和c3的取值分析

在主种群中引入了3个需要预先设定的参数，即参数学习因子c1,c2和c3，因此需要对3个参数进行取值分析。设置主种群的自我学习因子c1=2，社会学因子c2=2[22，23]，对学习因子c3选取了10个不同的数值。

表3给出了在c3不同的情况下，算法对10维和30维的5个函数的30次测试的最优结果，其中每个函数最好的结果用黑体字标出。

表3 主种群c3取值不同的优化结果Tab.3 Optimization result along with difference of c3 in master population

从优化结果来看，对10维的基准测试函数，除Sphere函数外，在c3=1.4时SMPSO算法的最优结果均优于其它情况；对30维的Sphere，Rastrigin，Schwefel函数，在c3=1.4时SMPSO算法的最优结果均优于其它情况。上述实验结果表明c3=1.4为主种群学习因子c3的最佳选择。在实际应用中，建议c3可在[1,2]取值。本文的实验中，c3取1.4。

3.3 与其它优化算法的性能对比

为了测试算法的寻优性能与适用性，对5个基准函数的10维和30维问题进行测试。并与7种其它改进PSO算法进行对比，包括：PSO(原始粒子群算法)[24]，WPSO(带惯性权重的粒子群算法)[24]，XPSO(带有收缩因子的粒子群算法)[24]，MiPSO[25]，MaPSO[25]，CLPSO[10]和RPCPSO[9]。其中，SMPSO算法子种群p3的参数组合设置为：w3=0.5，c31=2，c32=2；主种群学习因子参数的设置为：c1=2，c2=2，c3=1.4。本小节从优化结果、排名和收敛特征曲线展开讨论和分析。

表4和表5分别为PSO，WPSO，XPSO，MiPSO，MaPSO，CLPSO，RPCPSO以及SMPSO算法对10维和30维的基准测试函数寻优的求解结果。以表格的形式分别记录了30次实验的最优值(Max)、平均值(Mean)和标准差(SD)。其中最好的运行结果用黑体字标出。

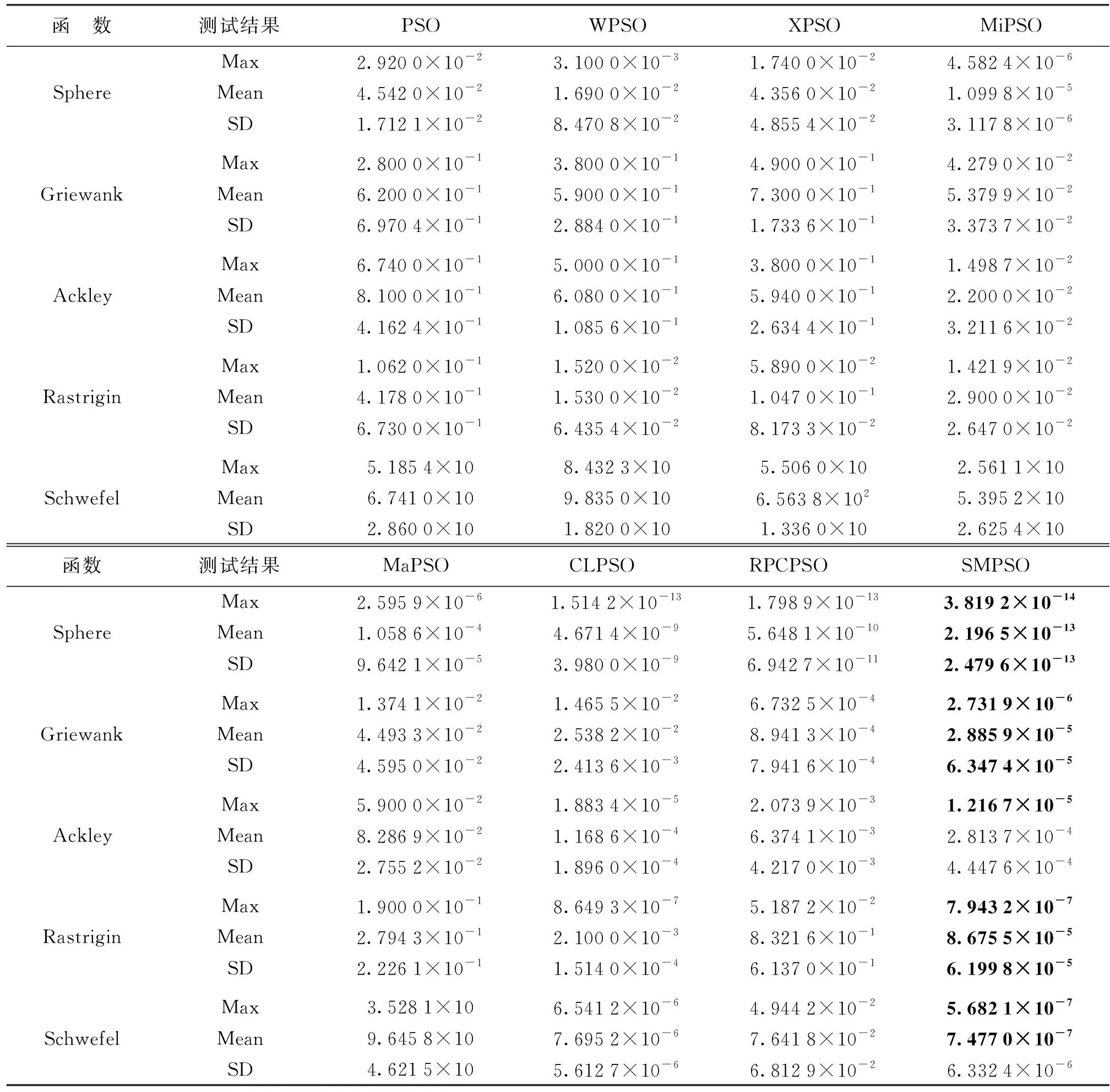
表4 10维函数的测试结果Tab.4 10 dimension function test result

表5 30维函数的测试结果Tab.5 30 dimension function test result

综上分析可知，在优化Sphere、Rastrigin、Griewank、Ackley、Schwefel函数时，SMPSO算法求解结果的最优值显著优于其它对比算法。同样从平均值的统计结果也能观察到与最优值相似的结论，即本文算法大幅度提高了PSO算法的优化能力。这得益于SMPSO算法采用的具有共生关系的主从群结构，从全局与局部提升了算法的搜索性能，同时自适应变异策略的引入，增大了算法跳出局部最优的能力。此外，本文算法所得结果的标准差在5个函数的测试中均比其它算法小很多，表明其结果具有更强的鲁棒性，说明SMPSO算法具有良好的全局动态寻优效果。无论从种群还是主种群，本文均选用了合适的参数组合，进一步提高了算法的搜索性能和解集的多样性。

为了更直接地比较各个算法，依据10维测试函数的优化结果，对改进的算法进行排名，如表6所示。得出SMPSO算法最优，CLPSO算法次之，接下来的3个算法依次为RPCPSO，MiPSO，MaPSO。

表6 8种优化算法基于优化结果的排名Tab.6 8 optimization algorithms based on ranking of optimization result

收敛特征曲线图反映优化结果随函数迭代次数变化的情况。图3～图5仅展示10维的Sphere函数和30维的Griewank，Rastrigin函数中算法优化结果收敛特征曲线，并以求解精度(AC)的对数形式呈现。观察图3～图5的收敛特征曲线可知，SMPSO算法寻优能力优于其它算法。在迭代初期，算法具有较大的搜索空间，SMPSO算法与其他算法的求解结果差异较大，SMPSO算法的求解精度明显较高。这得益于SMPSO算法从种群强大的全局搜索能力，给予了主种群寻找最优解的优势搜索领域。在迭代后期，当搜索空间逐渐减小，算法之间的差异减小，但SMPSO算法的求解精度仍具有明显优势。主要是因为主种群的局部精确搜索能力，使算法在小范围的搜索空间内，能够最快得发现最优解。

观察图3中SMPSO算法的收敛特征曲线可知，在400次迭代以后，算法寻优趋势减缓，逐渐陷入局部最优；但通过观察之后的收敛趋势发现，算法在520次以后的迭代中跳出了局部最优的状态。

同样在图4中也观察到了同样的结果，在算法600到1 000次迭代的收敛曲线中，算法产生两次跳出局部最优的动作。虽然在部分函数后期迭代中，SMPSO算法的寻优趋势减缓，但自适应变异策略引导算法不断跳出局部最优状态，提高了算法的寻优性能，从而使SMPSO算法具有优于对比算法的寻优结果。

相对其它改进的粒子群算法，SMPSO算法的主从群结构从多样性和搜索性能上使算法性能提升，自适应变异策略的引入提高了算法跳出局部最优的能力，实现了全局与局部搜索能力的同时加强，因而算法具有更高的搜索效率。

图3 10维的Sphere函数收敛特征曲线Fig.3 Convergence characteristic curves of 10 dimension Sphere function

通过与多种改进PSO算法实验结果的对比，本文提出的SMPSO算法具有一定的寻优优势。在大多数的测试函数中，SMPSO算法求解精度均高于对比算法，进一步验证了SMPSO算法的有效性。

图4 30维的Ackley函数收敛特征曲线Fig.4 Convergence characteristic curves of 30 dimension Ackley function

图5 30维的Griewank函数收敛特征曲线Fig.5 Convergence characteristic curves of 30 dimension Griewank function

4 结 论

本文从对多种群粒子群算法的研究入手，提出了一种基于速度交流的共生多种群粒子群算法(SMPSO)。在SMPSO算法中，针对算法的搜索性能和求解精度等问题，建立了具有共生关系的主从群结构，平衡了算法的全局与局部搜索能力。利用速度交流机制对从种群进行划分，该机制有效地提高了从种群的全局搜索性能。通过设定合适的惯性权值与加速因子的参数组合和引入自适应变异策略，进一步提升了主从群的搜索性能和跳出局部最优的能力。仿真实验表明SMPSO算法比其它改进算法在求解精度、搜索能力、稳定性等方面具有一定的优势，是一种高效的PSO改进算法。