基于GPS/MATLAB的AUV路径优化分析

2020-09-08吴志峰吴子岳

计量学报 2020年8期

吴志峰，吴子岳

(上海海洋大学工程学院，上海201306)

1 引言

随着我国海洋技术的发展，无线远程控制技术已经成为海洋环境监测的一种趋势，而移动测量也开始进入了研究范围，大部分的浅海定测系统分为单点检测和多点检测，但价格较昂贵。为了降低成本实现大面积的测量海洋水质环境，提出一种基于全球定位系统(GPS)/MATLAB规划路径的方法。

从模型建立方面考虑，综合评估重力、浮力、推力和水动力对水下航行器(autonomous underwater vehicle,AUV)的影响。本文基于合适的删选，建立了合理的6自由度水下航行器的动力学模型，设计一个精度合适的全球定位系统导航的路径规划方案。经过多次水下试验和MATLAB仿真，由GPS反馈给控制芯片STM32的实时定位数据，通过STM32处理MATLAB规划数据和GPS反馈实时定位数据，最终实现移动AUV的定位以及运行轨迹的选择，为纠正路径规划的路径偏差提供一种参考方法。

2 AUV模型建立

2.1 AUV结构

AUV的无人控制系统较为复杂,主要部分是一个能够携带各种视觉传感设备、探测装置、推进器，且能在水下空间运动的载体。水下机器人通常由控制系统、监察系统及载体3个部分组成。主要控制功能取决于水下机器人的具体功能，最简单的是由视频控制系统和用来反馈AUV运动。通过不断论证、反复试验，确定其结构组成为：电机式水下推进器4组(控制速度差以实现偏航、行进速度可调共有9档)、维持稳定性的翼片3组(后缘锋利、前缘渐变弧形以减小航行阻力)、57步进电机+丝杠滑台组合(滑台上的铅块前后滑动以控制航行器的重心并实现航行器的俯仰运动控制)、一体化玻璃钢球形端盖(便于密封及减阻)、φ160 mm耐压舱体、电控系统(中央控制器、STM32单片机、3组电机驱动模块、直流电池稳压模块)、同波段透明协议无线数据传输收发组件(C语言开发的的专用配套软件)、7.2 V飞思卡尔锂电池(8组)、AG332 GPS信标差分机、密封式航空插头及吊点紧箍等部件组成。AUV三维模型如图1所示。

图1 AUV三维模型Fig.1 3D model of AUV

2.2 AUV重心计算

将Cero中的总装模型以“parasolid”格式导入ADAMS多体动力学仿真软件中，对各部分已知参数和初始条件进行设置，包括质量、材料属性、转动惯量、初始速度以及初始位置等，并添加约束条件以及外载荷，对其进行运动仿真。平均密度为2.753 g/cm3,质量为18.85 kg，曲面面积为2.453 m2，重心在总体坐标位置为(x,y,z)=(-4.67，-4.63,-42.57)mm,AUV总体直径160 mm，总长度1 000 mm。

相对总体坐标系的惯性张量参数值见表1。

表1 惯性张量参数值

2.3 AUV的控制设计

AUV的无线传输系统由无线传输系统和GPS差分定位系统确定AUV在水下的运动测量和观察。由于水下作业要求精度较高，故AUV精度需要达到亚米级。本文AUV使用Trimble公司推出的AG332 GPS信标差分机进行GPS的定位，它自带GPS罗盘定位性能和姿势测量功能。采用无线传输模块(透明协议)通过串口RS232与其他通讯，通过TXD/RXD直接连接方式发送信号；分别与工控机、岸基的PC和GPS差分定位系统连接。调试接口通过TCP协议与工控机连接。当AUV的无线通讯模块参数设置后，通过透明协议传输信号，AUV上载体工控机和PC通过双向通讯实现数据无线传输。AUV上位机控制界面如图2所示，通过MSComm控件读取和发送RS232串口数据后，使用VB的字符段编辑函数，如Instr函数，截取数据中的指令，然后主控系统根据指令作出响应。每当系统检测到Start时，则系统开始截取指令；当系统截取到Over时，表明指令结束。在无线传输程序基础上，主控程序主要由字符段编辑函数组成，负责识别并响应数据中的指令，系统的响应又是主要通过STM32驱动程序。

图2 AUV上位机控制界面Fig.2 Host computer control interface of AUV

3 GPS定位系统

3.1 GPS定位系统设计

AUV控制系统体系结构图如图3所示，GPS定位系统主要由GPS差分定位模块、STM32控制模块、无线传输模块和PC机组成。在AUV航行后，AUV的上位机界面操作开始向定位模块下达接收定位数据命；GPS定位模块收到1/0数字信号后，模块执行命令，接收来自GPS卫星的数据信号，并通过无线传输系统过滤出数据文件；无线传输系统通过RS-232串口经过TXD/RXD数据传输线交叉连接方式将其传送给STM32；由STM32通过程序算法分离出经纬度、时间和海拔等信息，再通过RS232串口总线经过TXD/RXD直接连接方式传送给PC机处理及存储。信标差分机通过RS232接口与工控机相连，设置差分格式等参数后，工控机可以采集相关数据并且可以对数据进行处理。该系统采用的是Trimble公司推出的AG332 GPS信标差分机 GPS定位方案，如图4所示。

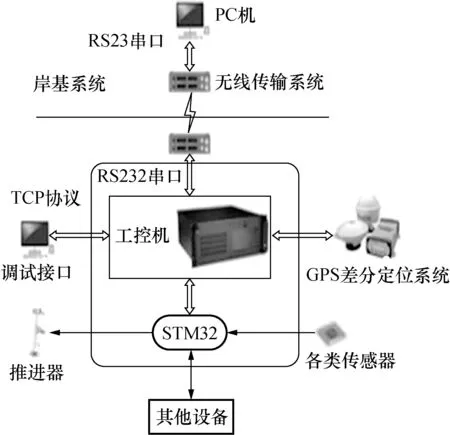
图3 AUV控制系统Fig.3 Control System of AUV

图4 定位方案设计Fig.4 Positioning scheme design of AUV

信标差分机主要通过DGPS模式进行全球定位，由GPS接收定位信号和信标机接收差分信息，信标机用来修正定位误差。全球定位系统要实现具体物体的定位，最少需要4颗GPSIII型卫星，其中3颗卫星需要确定物体具体在地球上的三维坐标，第4颗卫星需要修正卫星在大气和太空中所产生的误差，以此信息来修正定位误差。GPS使用的是美国的第三代GPSIII型卫星进行DGPS定位模式。本文实验采用民用C/A码。

3.2 定位系统模型

当水下机器人在水下前进时，其运动可以近似看成在二维平面上的运动，水下机器人从A点到达B点的运动模型为：

(1)

式中：v0为水下机器人的初始前进速度；θ0为水下机器人的初始方位角；点A为水下机器人的初始位置(x0,y0)，可由GPS/MATLAB定位均值测出。

当水下机器人由A点前进到B点时，GPS/MATLAB均值定位可以测出此时点B的相对位置(x1，y1)；同时，也可以通过运动模型推断出B点的相对位置，两个数据经过相互修正得出水下机器人的位置，提高系统整体的定位精度。

基于水下机器人的运动模型，构建水下机器人的定位系统模型，以下公式通过运动模型考虑在时刻差之间的具体坐标位置表达出水下运动坐标，如式(2)所示：

(2)

式中：状态变量x=[xd,yd,θd]T可以由GPS/MATLAB均值定位测量得到；xd是此时在x轴方向上的具体位置；yd是此时在y轴方向上的具体位置；θd是此时在倾角上的具体位置；Δd(k)是k时刻到k+1时刻水下机器人前进的距离；θ(k)为k时刻的运动方向；Δθ(k)为k时刻到k+1时刻水下机器人运行前进的转弯角度；ω为定位系统噪声，可认为在零均值状态下的高斯白噪声。

4 AUV运动模型建立

4.1 AUV受力分析

设计AUV的控制系统，首先需要构建AUV的动力学模型。本文主要参考重力、浮力、推力、和水动力对水下航行运动轨迹的影响。重力、浮力、推力以及水动力的表达式为：

(3)

式中:F表示受到的力；τ表示受到的力矩；θ表示水平方向的转角；φ表示垂直方向的倾角；G表示重力，这里取重心与坐标原点重合，故不产生重力矩。

(4)

式中:B表示水浮力;(xbybzb)T表示浮心在局部坐标系中的坐标。

第i个推进器产生的推力FTi：

(5)

式中:ρ表示水的密度；ni表示第i个推进器的螺旋桨转速；Di表示螺旋桨直径；KTi表示第i个推力器的推力系数。

推进器产生的合力和合力矩为

(6)

式中：Tx′、Ty′、Tz′表示沿x′、y′、z′轴方向上的合力；KT、MT、NT表示沿x′、y′、z′轴方向上的合力矩；RTi表示第i个推进器与之平行的坐标轴之间的垂直距离。

水动力和力矩为:

(7)

式中：Cd表示无因次阻力系数，对于大多数AUV，Cd=0.8～1.0；Sx′、Sy′、Sz′表示AUV分别垂直于x′、y′、z′轴的横断面面积;ur、vr、wr分别为x、y、z3个方向上的线速度。

水流产生的阻力矩与AUV角速度平方成正比，由试验测得阻力矩系数Kx、Ky、Kz后，可以求得流体对AUV产生的阻力矩在x′、y′、z′轴上的投影分别为Kx′、Ky′、Kz′。

4.2 AUV动力模型的建立

AUV动力学方程的矩阵表达式[6]为

(8)

5 水下实验与结果分析

根据建立的动力学模型和控制系统，采用MATLAB和SIMULINK对水下机器人以恒定速度跟踪期望轨迹和GPS观察规划路线进行比较。AUV外形简化为直径0.16 m、长1 m的均质圆柱体。水流的速度均为0.1 m/s，同时假定浮心和重心重合。假设水下航行器从坐标(0,0)到坐标(30,30)处沿直线运动，全球定位系统在实际监控点测得的3处监控位置经纬度为(30.879 9 N,121.910 0 E)，(30.879 6 N,121.922 3 E)，(30.879 6 N,121.924 3 E),此时全球定位系统规划的路线经纬(30.879 9 N,121.910 0 E)，(30.879 9 N,121.928 3 E)，(30.881 9 N,121.929 3 E)，其中，N表示为北纬，E表示为东经。

AUV实验结果如图5所示，能够根据AUV的当前状态，利用MATLAB指导AUV的路径规划，从而响应速度快，能够相对比较稳定和准确的规划路线，验证MATLAB控制器的稳定性以及灵活性。

图5 路径曲线图Fig.5 Path graph

图6为经纬测试数据图。图6中，可以根据AUV从坐标原点以0.2 m/s的速度追踪目标，AUV目标轨迹是采用MATLAB和SIMULINK跟踪期望，MATLAB同时接受GPS反馈的坐标信息，通过MATLAB和GPS双坐标取双坐标中值方法，通过闭环控制反馈给STM32控制芯片处理及时调整AUV路径进行航行。比较MATLAB测试数据、GPS测试数据、真实测试数据和均值测试数据，测试结果显示:基于MATLAB/GPS均值处理后路径更加平稳,精确度更高。

图6 经纬测试数据图Fig.6 Test chart of warp and weft

在AUV浅水下水试验过程中，由如图6得到四方差分析数值，实际测试数据为K，GPS测试数据为K1，MATLAB测试数据为K2以及均值测试数据为K3。以实际测试数据为参考依据，经过方差分析得出K1为(1.020×10-8,2.060×10-8),K2为(1.070×10-6,2.070×10-10)，K3为(1.070×10-6,1.070×10-10)。均值处理在保持稳定性上，在y轴精确性改善上有明显提高。