抄板结构对纤丝状生物质颗粒流动特性的影响

2020-09-08顾丛汇姚寿广袁竹林

江苏科技大学学报(自然科学版) 2020年4期

顾丛汇,姚寿广,袁竹林

(1.江苏科技大学能源与动力工程学院,镇江 212003)(2.东南大学能源与环境学院,南京 210096)

转筒烘干机具有处理能力大、可操作性强、密封性好、燃料消耗低等优势,被广泛应用于化工、食品、水泥、冶金、矿产等领域[1]．湿颗粒在转筒烘干机内的干燥过程不仅与气-固两相间的热质传递有关,还涉及复杂的多相流动问题．颗粒的流动特性可直接影响其传热传质效率,尤其是针对柔性颗粒，其中,以柔性纤丝状颗粒为代表,其形状细长,在结构上异于粉末状或球形颗粒,因此大大增加了纤丝状颗粒在多相流动过程中受力和碰撞的复杂性和研究难度,转筒烘干机内部的气固两相流动问题引起了国内外学者广泛关注[2-3]．

目前,由于计算机高速发展以及受到传统测试手段的限制,对转筒烘干机内部颗粒运动规律的研究大部分基于数值模拟方法[4-9]，但对纤丝状颗粒运动的理论研究还不够完善,尤其是在大量丝状颗粒运动方面,很多问题有待于进一步研究和探讨．

文中采用实验与数值模拟相结合的技术路线,研究纤丝状生物质颗粒在冷态转筒内的流动状态，当纤丝状生物质颗粒大量存在与流场中,颗粒间非常容易出现聚集、缠绕和结团等问题而影响其流动形态，因此提出了一种解决大量纤丝状颗粒运动特性的数值建模与计算的新方法，将堆积后的若干纤丝状生物质颗粒视为“虚拟颗粒团”来处理，同时假设该颗粒团内所有颗粒的运动状态保持一致,位于颗粒团内的颗粒之间无干扰[10-12]．在上述运动数学模型中,重点考察了重力、摩擦力、颗粒团间碰撞力、气固间相互作用力．利用Visual Basic程序语言对以上数理模型进行编程求解．结合实验方法,验证该建模方法的合理性和可行性．通过数值模拟方法对纤丝状颗粒在转筒烘干机内停留时间分布进行分析，得出抄板结构对纤丝状颗粒的流动特性的影响规律．

1 计算模型和数值方法

在工业生产领域中,常见的转筒烘干机由回转体、抄板、支架,以及传动等装置构成．筒体与水平方向以一定角度倾斜,待干燥物料由较高一侧端口进入转筒烘干机,在抄板的作用下不断地被抄起、抛洒,循环往复运动直至到达另一侧端口被排出．文中采用欧拉-拉格朗日相结合的数值模拟方法,研究纤丝状颗粒在转筒烘干机内的运动特性．

1.1 计算模型建立

当大量的纤丝状生物质颗粒进入转筒烘干机时,颗粒在运动过程中极易出现缠绕,导致结团后的颗粒群保持相同的运动状态继续流动．因此,将相同运动状态的颗粒群视为一个“虚拟颗粒团”,基于离散单元法,跟踪计算每个“虚拟颗粒团”的运动轨迹．图1为纤丝状颗粒在转筒烘干机内运动的物理模型．

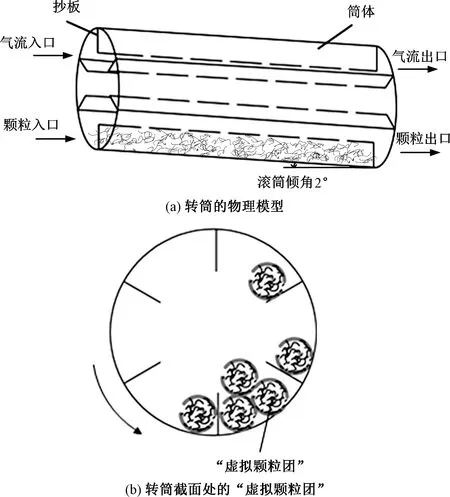
图1 纤丝状颗粒在转筒烘干机内运动的物理模型Fig.1 Physical model for flexible filamentous particle in a rotary dryer

在实际工艺过程中,团聚后的颗粒团之间仍会在运动过程中发生碰撞．颗粒群在转筒内不断地接触,相互影响各自的运动轨迹和流动状态,在此过程中产生的力属于固体力．为了更好地计算多个颗粒团碰撞后的运动规律,采用软球模型处理“虚拟颗粒团”之间的碰撞．通过文献[13],软球模型是与实际情况最为吻合的一种处理颗粒碰撞的方法．因此，文中对颗粒运动、气相流动、颗粒团间碰撞以及气固间相互作用力展开分析,并建立数学方程．

1.1.1 颗粒动力学方程

基于离散单元法,考察每个计算时间步长中颗粒的受力情况,建立颗粒团动力学方程．颗粒团在气相流场中的运动分为平动和转动．基于牛顿第二定律,可得:

(1)

(2)

式中：v为颗粒团平动速度,m/s;g为重力加速度,g=9.8 m/s;Ftotal为颗粒团受到的合外力,N;ω为角速度,rad/s;Ttotal为颗粒团受到的合力矩,N·m;I为转动惯量,kg·m2．

1.1.2 气相流动数学方程

在复杂的气固流动体系中,颗粒相和气相场之间的运动相互耦合．基于局部平均法[13-14],得到气相场连续性方程和动量守恒方程:

(3)

εPgas+ερgasg+Sm

(4)

式中：ε为空隙率,%;ρgas为气相密度,kg/m3;ugas为气相速度,m/s;τgas为气体应力张量;Pgas为气相压力,Pa;Sm为源项．

1.1.3 颗粒团碰撞作用力

在处理“虚拟颗粒团”之间的碰撞问题时，假设“虚拟颗粒团”与边界之间发生碰撞且维持一定时间,使得“虚拟颗粒团”在碰撞的过程中存在一定程度上的重叠．以颗粒团i和颗粒团j的碰撞为例．

首先,判断颗粒团之间的碰撞情况．若为弹性对心碰撞,如图2．

图2 对心碰撞Fig.2 Central collision

在该情况下,颗粒团i和颗粒团j在接触点上发生弹性变形．对颗粒团i而言,在运动方向上受到颗粒团j对其的阻力,反之亦然;该阻力与其法向变形位移和颗粒的刚度成正比关系．当颗粒团i达到最大变形时停止运动,与此同时,在上述阻力的作用下出现沿原运动方向“反弹”的倾向．

若为偏心碰撞,颗粒团碰撞前后如图3．

图3 偏心碰撞Fig.3 Eccentric collision

将碰撞接触力fC,ij沿法向和切向划分,其中,法向分力fCn,ij的作用与上文对心碰撞过程相似;切向分力fCt,ij使得颗粒团在球心处产生一个力矩,发生旋转运动．在上述模型中,一旦涉及多个颗粒团间相互碰撞时,对各个颗粒团之间的碰撞分别进行计算,利用矢量叠加处理即可．

若i颗粒团与j颗粒团发生非完全弹性碰撞时,碰撞后颗粒团的动能会存在部分消耗．该部分损失量不仅与颗粒的物理特性和碰撞时颗粒间的相对速度紧密相关,而且由颗粒团碰撞后受到的反向作用力决定．颗粒团在接触面是否发生滑移由两者之间的切向分力决定．若|fCt,ij|>μ|fCn,ij|,碰撞的颗粒团在接触面上发生滑移．当两个旋转的颗粒团发生偏心碰撞时,除了计算法向与切向位移之外,还需要得到颗粒自转时刻在碰撞点处的切向速度．同理可得,当多个颗粒团发生碰撞时,各参量采用矢量叠加法计算统计．

fC,ij=fCn,ij+fCt,ij

(5)

fCn,ij=(-knδn,ij-ηnvr,ij·nij)nij

(6)

fCt,ij=-ktδt,ij-ηtvs,ij

(7)

vs,ij=vr,ij-(vr,ij·n)n+r(ωi+ωj)·n

(8)

式中：δn,ij、δt,ij分别为颗粒团的法向、切向变形量,m;kn、kt为法向、切向的弹性系数;ηn、ηt为法向、切向的阻尼系数,由恢复系数e等参数确定;vr,ij为两个颗粒团的相对速度,m/s;vs,ij为颗粒碰撞点的滑移速度,m/s;nij为单位法向量;ω为旋转角速度,rad/s．

由于滑移而产生的切向分力为:

fCt,ij=-μs|fCn,ij|tij

(9)

式中：tij=vs,ij/|vs,ij|,μs为滑动摩擦系数．

1.1.4 气-固间作用力

在气固两相流动系统中,气-固间相互作用极其复杂,包括附加质量力、浮力、巴赛特力、马格努斯力、萨夫曼升力、曳力、压力梯度力等作用力[15]．为了简化数理模型,在现阶段的研究中仅考虑颗粒与气流之间的曳力,后续研究中会进一步考虑其他气固间作用力．当气流绕流颗粒团且两者存在速度差|uf-upi|,颗粒团i受到的曳力记为FDi

(10)

CD=CDSPζ

(11)

式中:FDi为颗粒团的曳力,N;uf为气流速度,m/s;upi为颗粒团沿气流方向的速度,m/s;CD为颗粒团曳力系数,该曳力系数与雷诺数有关,可由以下两种方法计算得出:方法一,根据牛顿通过大量实验而获取的数据,并且经过后人多次验证得出,雷诺数介于700～2×105之间,CD为常数,即CD=0.44[15];方法二,由文献[16]提出的公式计算得出；CDSP为基于统计的当量球形颗粒的曳力系数;ζ为非球形修正系数,文中选择表面粗糙的球形颗粒,ζ=2.42[16];A为颗粒团的横截面积,m2;ρ为颗粒团密度,kg·m-3,模拟中采用纤丝状颗粒的堆积密度．

(12)

(13)

1.2 算例验证

1.2.1 实验装置与设计

采用中试冷态转筒实验系统对纤丝状生物质颗粒的平均停留时间进行测试，该实验系统由喂料、传输、进料和输运4个部分组成,实验装置如图4．采用的实验材料初始湿基含水率为15%,质量流量为30 g·s-1;长度为14 mm,宽度为1 mm的柔性纤丝状烟丝颗粒为实验原料,如图5．

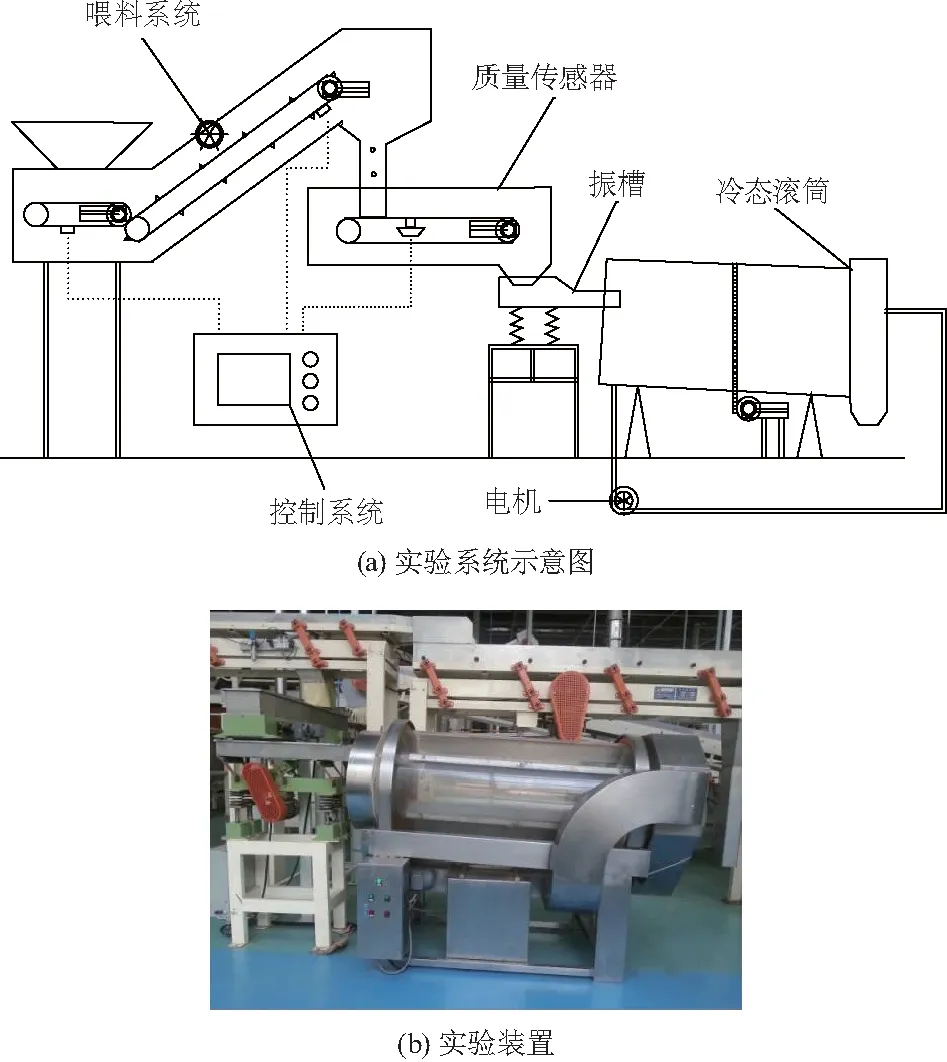
图4 实验系统示意图与装置Fig.4 Experimental setup and its schematic diagram

(14)

1.2.2 模拟参数的确定

为了确定上述模型中“虚拟颗粒团”的尺寸,随机选用一组工况设计实验,基于冷态转筒烘干机实验平台,以纤丝状的烟丝颗粒为实验材料,测量烟丝颗粒在转筒内运动过程中的平均停留时间．物理模型按实验尺寸构建,计算颗粒在转筒内的平均停留时间,模拟条件如表1．

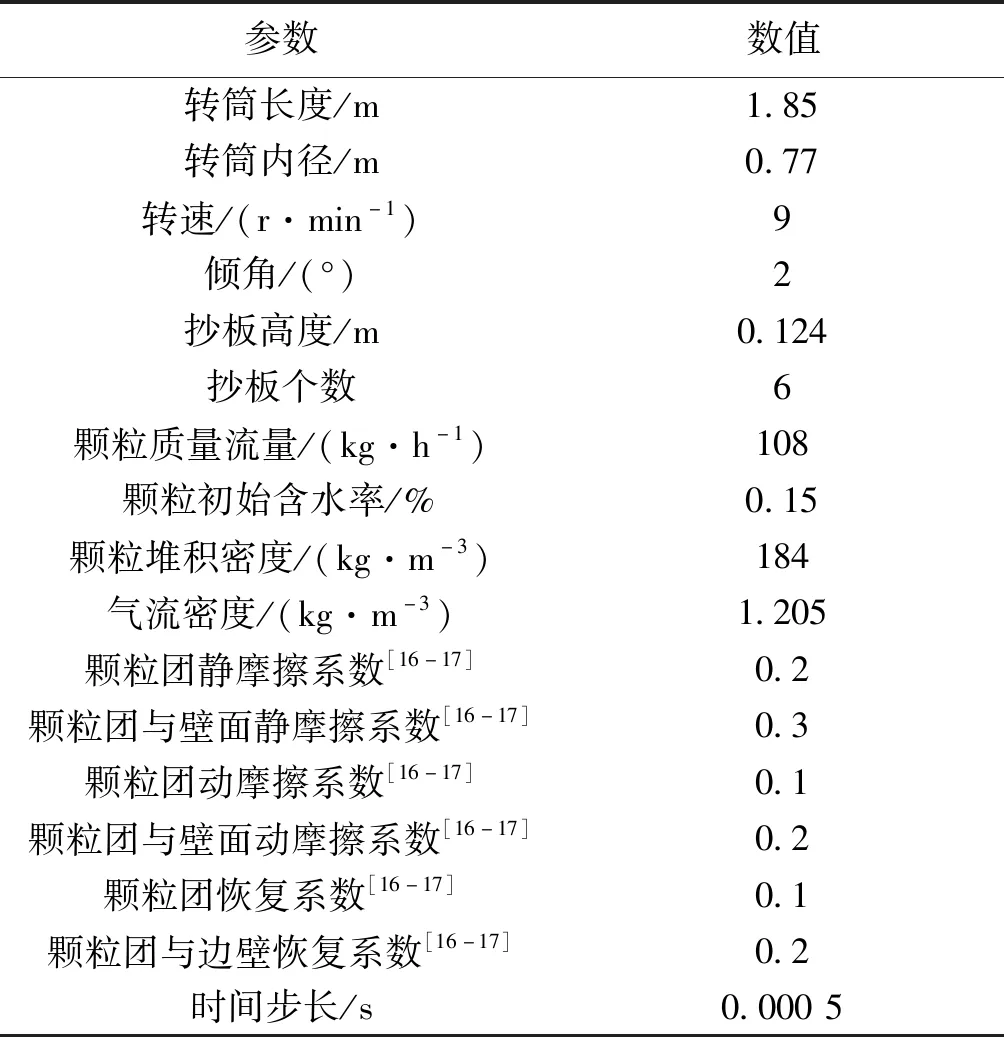
表1 数值模拟条件Table 1 Simulation condition

不难发现:在相同的颗粒质量流量条件下,“虚拟颗粒团”的粒径越大,模拟计算时间越短．当“虚拟颗粒团”粒径低于0.03 m时,转筒内的颗粒数量大,颗粒之间相互剧烈碰撞,导致其在转筒内的平均停留时间减少．

图6 “虚拟颗粒团”粒径dv与平均停留时间关系Fig.6 Effect of suppositional particle group diameter on mean residence time

图7 “虚拟颗粒团”粒径dv与模拟计算时间t的关系Fig.7 Effect of suppositional particle group diameter on simulating time

模拟结果与实验值偏差较大,单一工况所需模拟计算时间超过16 h．由图6可见,当“虚拟颗粒团”的粒径为0.03～0.045 m时,模拟与实验结果之间的误差均在可允许误差范围内,模拟计算时长为小于14 h．随着“虚拟颗粒团”粒径的增加,在相同的质量流量下,筒内颗粒数量降低,颗粒间碰撞概率也随之降低,模拟结果不满足要求．

综合考虑单一工况所需计算时间和颗粒平均停留时间这两个主要参数,文中模拟计算纤丝状颗粒运动状态时选取的“虚拟颗粒团”粒径为0.03 m．

1.2.3 算例验证

根据所构建的“虚拟颗粒团”模型,计算颗粒在转速N分别为7、10和13 r·min-1条件下的平均停留时间,将数值模拟结果分别与实验值和基于Friedman-Marshall模型[18]经验公式(15)计算结果比较,结果如图8．

(15)

图8 纤丝状颗粒平均停留时间的经验公式、实验和模拟结果对比Fig.8 Comparison among empirical formula, experimental and numerical results on mean residence time of flexible filamentous particle

结果表明:通过F-M模型经验公式所计算出的结果与实验数据之间的偏差较大,尤其是在转速为7和13 r·min-1的情况下,两者误差超过20%．因此,传统的F-M模型无法适用于纤丝状这类非球形颗粒在转筒干燥器内的停留时间的预测．文中建立的数值模拟新方法得到的计算结果与实验的误差低于10%．由此可见，采用纤丝状颗粒集合成“虚拟颗粒团”的方法来解决大量纤丝状颗粒的计算是满足条件的，不仅可以用于工业生产规模颗粒量的计算模拟,还能缩短数值模拟的计算时间,提高计算效率．

2 结果与讨论

文中研究抄板结构对纤丝状颗粒运动特性的影响,计算不同抄板高度(0.064、0.094、0.124、0.154 m)和抄板个数(2、4、6、8)条件下,纤丝状颗粒的停留时间分布和平均停留时间与抄板结构之间的关系．

2.1 抄板高度对纤丝状颗粒运动特性的影响

纤丝状颗粒在转筒内的停留时间分布(图9)能够清楚的展现出:在不同抄板高度的作用下,纤丝状颗粒的停留时间分布结果呈正态分布,与文献[19-21]对颗粒在转筒干燥设备内停留时间分布的研究结果相一致．

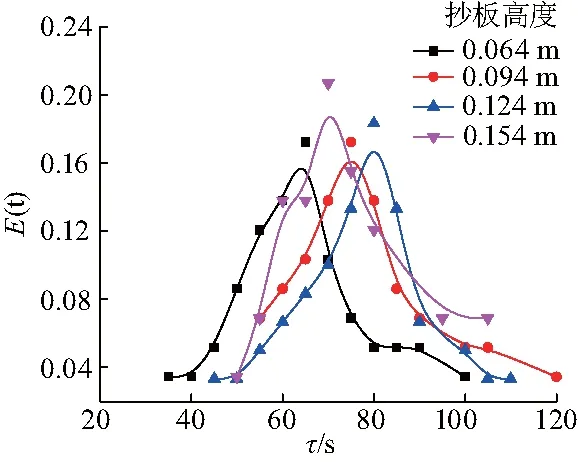
图9 不同抄板高度下纤丝状颗粒的停留时间τ分布曲线Fig.9 Effect of flight height on flexible filamentous particle residence time

在丝状颗粒容积率为1.3%的情况下,当抄板高度与转筒内径之比a介于0.17～0.32之间,丝状颗粒停留时间分布的位置参数μ(即用于描述正态分布集中趋势的位置)大小随抄板高度的增加而增加;颗粒混合均匀性较好,其平均停留时间增长缓慢,颗粒沿转筒轴向扩散速度减弱．当a>0.32时,颗粒停留时间分布更集中,μ值不升反降,颗粒在抄板上的停留时间快速增加,颗粒平均停留时间急剧增加,纤丝状生物质颗粒运动一致性增强．抄板高度与转筒内径之比与位置参数之间关系和变化规律如图10．

图10 抄板高度与转筒内径之比a与位置参数μ之间的关系Fig.10 Effect of locate parameter on ratio of flight height and drum diameter

通过对纤丝状颗粒在转筒内平均停留时间的实验和模拟分析可得:颗粒在转筒内的平均停留时间随抄板数目的增加而增加,结果如图11．文中由于忽略了丝状颗粒在运动过程中的团聚程度、颗粒交换、重组等复杂因素,使得模拟得到的颗粒平均停留时间略低于实验值,但是该误差值在可允许的范围内．在颗粒容积率<0.015、a>0.4的条件下,纤丝状颗粒沿转筒轴向扩散速度降低,并且在该方向颗粒运动一致性更好;颗粒在径向作圆周运动时间增加,颗粒群混合性较差,导致模拟结果高于实验值．

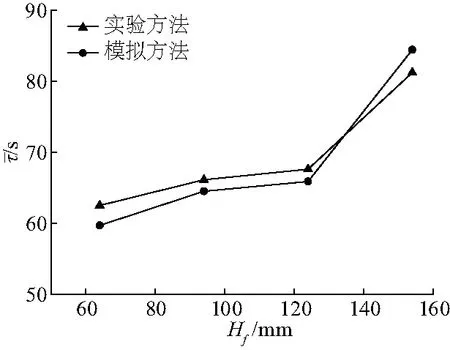
图11 不同抄板高度下颗粒平均停留时间的数值模拟与实验结果对比Fig.11 Comparison of numerical and experimental results on the mean residence time under the condition of flight height

因此，所建立的纤丝状颗粒运动模型在颗粒运动平均停留时间和停留时间分布的模拟计算是合理的,当a<0.32时,抄板高度对颗粒平均停留时间的影响较小;当a>0.32时,纤丝状颗粒在设备内的停留时间分布更加集中．通过模拟结果与实验值的对比分析,文中方法可大大降低实验导致的时间、资源和成本耗费,同时可为合理确定转筒抄板高度范围以便优化转筒生产效率奠定理论基础,并提供一定的指导．

2.2 抄板数目对纤丝状颗粒运动特性的影响

为了进一步探讨抄板数目对纤丝状颗粒运动特性的作用,采用数值新方法模拟不同抄板数目下颗粒的运动规律．图12给出了抄板数目对纤丝状颗粒的停留时间分布变化的影响．由图可知,在不同抄板数目的情况下,颗粒在转筒内的停留时间分布曲线均呈现出正态分布趋势．抄板数目越多,颗粒停留时间分布曲线中的对称轴所处的停留时间越大,颗粒混合越均匀．其中,抄板数目n与位置参数μ之间的关系如图13,可以看出，抄板数目越多,μ值越大．当抄板数目n=4和n=6的情况下,两者位置参数较为接近;而抄板数目n=6时,纤丝状颗粒停留时间的离散程度高于n=4的工况．

图12 不同抄板数目下纤丝状颗粒的停留时间分布Fig.12 Effect of flight number on flexible filamentous particle residence time

图13 抄板数目n与位置参数μ之间的关系Fig.13 Effect of locate parameter on flight number

从纤丝状颗粒的平均停留时间与抄板数目之间关系的实验与模拟结果(图14)可知,转筒内置抄板数量越多,颗粒在抄板上的滞留时间越久，导致颗粒在转筒横截面上随筒体作圆周运动的时间越长,增加颗粒在转筒内的平均停留时间，颗粒在转筒内运动一致性受到抄板结构的影响.通过研究发现在一定范围内增加抄板数量能加强纤丝状生物质颗粒群运动的一致性,强化气固间相互扰动,使得颗粒混合更均匀,且颗粒的停留时间更集中．当n=2～6时,模拟结果与实验值总体上比较吻合;由于建模中忽略了“虚拟颗粒团”内部丝状颗粒的流动与颗粒间相互碰撞,导致模拟值略低于实验值．当转筒内抄板数目增加至8块,颗粒在转筒底部停留时间增加,加之在抄板的作用下,颗粒在抄板上的滞留量也增多,延长了颗粒在截面处的运动时间．因此，增加抄板数目能够提高丝状颗粒团聚、重组的概率,使得颗粒沿轴向扩散速率增加，从而导致颗粒平均停留时间的模拟值高于实验值．

综上所述,对纤丝状颗粒而言,在一定范围内增加抄板数目,有利于提高颗粒间的混合作用,从而降低颗粒堆积、聚团等现象发生的概率．

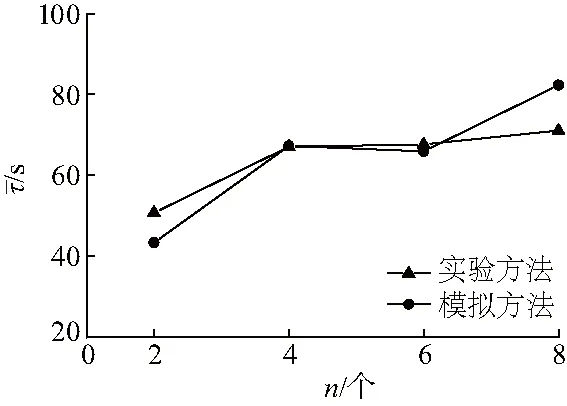
图14 不同抄板数目下颗粒平均停留时间的数值模拟与实验结果对比Fig.14 Comparison of numerical and experimental results on the mean residence time under the condition of flight number