基于主客观综合定权法的单值中智TODIM决策方法

2020-09-08霍礼勇

江苏科技大学学报(自然科学版) 2020年4期

刘菊,李鹏,霍礼勇

(江苏科技大学经济管理学院,镇江212003)

由于经济社会的复杂性,传统的精确数已经很难解决现实决策问题．文献[1]中提出以隶属度表征不确定性信息的模糊集,该理论已被应用于社会的诸多领域．因为模糊集仅用隶属度一个单维信息来表征模糊信息,难以解决带有犹豫情况的决策问题．文献[2]中提出以隶属度、非隶属度来表征不确定性信息的直觉模糊理论,使得决策者在刻画不完全及模糊信息方面更加合理．目前,相关理论与实践研究已取得大量的成果[3-10]．

尽管直觉模糊理论得到了深入研究,解决了很多多属性决策中信息的犹豫性问题,但在实际问题中仍存在其不能表征的不确定性信息．文献[11]中提出中智集的概念,运用真实程度函数TA(x)、不确定程度函数IA(x)和谬误程度函数FA(x)来刻画决策者对客观事物的看法．其中,TA(x)、IA(x)、FA(x)均属于] 0-,1+[范围内的标准或非标准实数子集．虽然中智集泛化了模糊集和直觉模糊集,但由于其范围问题,难以直接应用于现实科学和工程领域．针对上述问题,文献[12]中定义了单值中智集的概念．文献[13]中提出了单值中智集的距离、相似度及熵的测度公式．文献[14]中提出了一种新的单值中智集加权距离公式．文献[15]中参照文献[16-19]，对单值中智集的记分函数进行了定义．文献[20]中针对文献[15]中提出的记分函数，引入参数进行改进,定义了新的记分函数．单值中智集作为刻画模糊信息的有效工具广泛应用于多属性决策中．文献[21]中定义了单值中智集的相关系数,并提出了一种多属性决策方法．文献[22]中采用加权平均算子集结专家意见确定属性权重,并与TOPSIS方法结合，对供应商进行选择．文献[23]中定义了一种新的交叉熵公式以确定属性权重,并在此基础上构建了一种新的多属性群决策模型．文献[24]中基于中智熵确定属性权重,利用加权平均算子集结群体信息,结合VIKOR方法处理单值中智集多属性群决策问题．

上述研究丰富了单值中智集理论,提供了宝贵的理论经验,但是在属性权重研究方面,大多数文献往往直接给出属性权重[14,28],或者仅单方面主观定权[22]或客观定权[15,23-24]．主观定权法是专家基于自身认知对属性在系统内的相对重要程度作出的主观判断,可以充分利用专家的自身知识及个人偏好,但不可避免具有一定的主观随意性,因而其得出的权重的可信度可能遭受到质疑;客观定权法的数据直接来自决策矩阵,不依赖于决策主体的主观判断,所求得的权重具有客观性,但当决策矩阵确定后,无论决策背景如何改变,权重不变,这完全违背了决策的基本规律．因此,合理的权重应综合考虑决策矩阵和专家偏好,即主客观综合定权．文中通过DEMATEL方法确定主观权重,根据熵权法确定客观权重,采用线性加权法确定综合权重．

由于人们在决策过程中往往难以做到完全理性,决策过程应充分考虑人的有限理性因素．TODIM方法是基于前景理论提出的行为决策方法,该理论自提出以来便引起诸多学者的关注．文献[25]中将TODIM方法运用到随机直觉模糊数多属性决策问题．文献[26]中提出了基于云模型和TODIM方法的多属性决策模型,该方法通过集结多个专家的决策信息来处理犹豫语言信息的机器人选择问题．文献[27]中考虑到生活中不确定及不精确信息常用直觉模糊语言变量表示,构建了基于直觉模糊语言变量的TODIM方法．文献[28]中将TODIM拓展到区间数中,构建区间TODIM多属性决策方法,解决旅游景区的应急疏散决策问题．文献[29]中以互联网消费为背景,基于商品评论信息,构建概率语言TODIM方法,用以处理互联网背景下消费者产品选择问题．

国内外对TODIM方法的研究成果中,TODIM方法在单值中智集多属性决策问题方面研究较少．文献[30]中基于单值中智集的距离公式和文献[15]中提出的记分函数，将TODIM方法拓展到单值中智集领域,虽然上述模型充分考虑了决策者的决策心理,但该模型引用的记分函数存在不合理的地方,而且属性权重直接给出，并未给予确定属性权重的合理方法．因此,文中将TODIM方法进一步拓展到单值中智集领域,解决单值中智集多属性决策问题．

1 基本概念

1.1 中智集理论

定义1[24]设X为非空集合,x为其中任意元素,X上的中智集A可以由真实程度函数TA(x)、不确定程度函数IA(x)及谬误程度函数FA(x)表示,其中TA(x)、IA(x)和FA(x)是]0-,1+[的标准或非标准实数子集,即TA(x):X→] 0-,1+[,IA(x):X→] 0-,1+[,FA(x):X→] 0-,1+[．其中非标准有限数1+=1+ε,1是它的标准部分,ε>0为无穷小数,是它的非标准部分,且0-≤supTA(x)+supIA(x)+supFA(x)≤3+．

定义2[12]设X为非空集合,x为其中任意元素,X上的单值中智集A可表示为:

(1)

式中,TA(x),IA(x),FA(x)∈[0,1 ],并满足0≤supTA(x)+supIA(x)+supFA(x)≤3．单值中智数记为a=〈Ta(x),Ia(x),Fa(x)〉．

(2)

且满足:

(1)d(A,A)=0;

(2)d(A,B)=d(B,A);

(3) 0≤d(A,B)≤1．

定义4[31]设a=〈Ta(x),Ia(x),Fa(x)〉和b=〈Tb(x),Ib(x),Fb(x)〉是任意两个单值中智数,其运算规则如下:

(1)λa=〈1-(1-Ta(x))λ,(Ia(x))λ,

(Fa(x))λ〉;λ>0.

(2)aλ=〈(Ta(x))λ,1-(1-Ia(x))λ,1-(1-Fa(x))λ〉;λ>0.

(3)a⨁b=〈Ta(x)+Tb(x)-Ta(x)·Tb(x),Ia(x)·Ib(x),Fa(x)·Fb(x)〉.

(4)a⊗b=〈Ta(x)·Tb(x),Ia(x)+Ib(x)-Ia(x)·Ib(x),Fa(x)+Fb(x)-Fa(x)·Fb(x)〉.

FA(xi)·|IA(xi)-IAC(xi)|)

(3)

1.2 DEMATEL算法

决策试行与评价实验室(decision making trial and evaluation laboratory,DEMATEL)算法提出是为了解决社会经济中的复杂系统问题[32],算法步骤概述如下:

(1) 构造直接影响矩阵．设某复杂系统中有n个因素,专家基于自身知识以及个人偏好依次对因素间的影响强度进行两两比较,设因素Ci对Cj的影响强度为aij,其中,当i=j时,aij=0,即直接影响矩阵为:

(4)

(3) 计算综合影响矩阵．具体算式为:

B(I-B)-1=[tij]n×n

(5)

式中,I为单位矩阵．

(4) 计算中心度和原因度．将综合影响矩阵按行相加,求得该因素对系统内其他因素的影响程度为:

(6)

将综合影响矩阵按列相加,求得该因素受到系统内其他因素的影响程度,公式为:

(7)

则中心度Gj和原因度Uj分别为:

Gj=Rj+Cj

Uj=Rj-Cjj=1,2,…,n

(8)

式中,中心度Gj为第j元素在该系统中的相对重要程度,Gj越大,表示该元素在系统中对其他因素及受其他因素的综合影响越大,则在系统中重要程度越高;反之,重要程度越低．当原因度Uj<0时,该元素为结果因素；Uj>0时，该元素为原因因素．

2 新的记分函数

2.1 现有记分函数缺陷

单值中智数通过运用真实程度函数TA(x)、不确定度函数IA(x)及谬误程度函FA(x)表征不确定性信息,记分函数是对单值中智数进行大小比较的有效工具．

文献[15]在文献[16-19]的基础上,对单值中智数的记分函数定义为:

S(a)=(Ta(x)+1-Ia(x)+1-Fa(x))/3

(9)

文献[15]认为真实程度越大，且不确定程度及谬误程度越小,则记分函数越大．该记分函数虽然对单值中智数中的Ta(x)、Ia(x)及Fa(x)进行了充分考虑,但仍存在不合理之处．下面给出一个反例证明其不足之处:

例1设单值中智数a=〈0,1,0〉,b=〈0,0,1〉,显然a优于b．但通过上述记分函数计算得:

即S(a)=S(b)．

文献[20]对文献[15]的记分函数进行了修正,加入了参数α,β(0<α<β≤1),定义记分函数为:

(10)

文中规定α=0.3,β=0.4,该记分函数尽管通过参数调节不确定程度及谬误程度,但是对参数取值缺乏理论依据．

2.2 新的记分函数

在直觉模糊数的研究中,文献[33-34]运用不同方法确定了隶属度与非隶属度之间的比例关系,对犹豫度进行了客观合理的分配,分别提出了基于直觉模糊数的记分函数公式．文中借鉴以上思想,定义了基于单值中智数的新记分函数公式．

定义6设X为非空集合,x为对象集X中的元素,单值中智数a=〈Ta(x),Ia(x),Fa(x)〉,则a的记分函数式为:

SNEW(a)=Ta(x)-Fa(x)+

(11)

式中：Ta(x)为真实程度；Ia(x)为不确定程度；Fa(x)为谬误程度；Ta(x)-Fa(x)为净真实程度．根据文献[35],a+=〈1,0,0〉为绝对真实,a-=〈0,1,1〉为反真实．d(a,a+)为中智数a=〈Ta(x),Ia(x),Fa(x)〉与a+=〈1,0,0〉的距离,即a=〈Ta(x),Ia(x),Fa(x)〉到绝对最大值的距离．因此,d(a,a+)越小,1-d(a,a+)越大,则a=〈Ta(x),Ia(x),Fa(x)〉与绝对真实的接近程度越高,即不确定程度Ia(x)中属于真实部分越多．Ta(x)=1,Ia(x)=0,Fa(x)=0时,d(a,a+)=0,1-d(a,a+)=1．同理,d(a,a-)为中智数a=〈Ta(x),Ia(x),Fa(x)〉与a-=〈0,1,1〉的距离,d(a,a-)越小,1-d(a,a-)越大,则表示a=〈Ta(x),Ia(x),Fa(x)〉与反真实的接近程度越高,即不确定程度Ia(x)中属于谬误部分越多．因此,真实程度与谬误程度的比例之差为:

采用例1的数据来验证文中提出的记分函数的合理性．根据式(2)分别求出d(a,a+)、d(a,a-)、d(b,a+)、d(b,a-),具体过程:

由上述结果可知S(a)>S(b),因此a优于b,符合常理．

文中提出的新的记分函数利用中智数中的真实程度与谬误度之间的比例关系对不确定程度进行分配,充分挖掘了不确定部分的真实信息和谬误信息,并将这些信息与原真实信息和谬误信息充分融合,实现了中智数间的有效比较．

3 基于主客观综合定权法的单值中智TODIM决策方法

对于某单值中智集多属性决策问题,有m个方案Ai={A1,A2,…,Am},n个属性Cj={C1,C2,…,Cn},决策者给出的决策矩阵为D=[dij]m×n,其中,dij=〈Tij(x),Iij(x),Fij(x)〉为方案Ai在属性Cj下的评估值,以单值中智数形式表征．

3.1 权重确定

3.1.1 主观权重确定

由于专家在给出直接影响矩阵时,不仅基于严密的逻辑推理,还依靠专家的自身知识、个人偏好等非理性因素,因此专家基于实数对两属性之间的影响强度进行判断的过程带有不确定性．在单值中智集理论中,决策者使用TA(x)、IA(x)及FA(x)来表征其对客观事物的看法,更贴切刻画出决策者对决策信息的认识,因而将单值中智集运用到DEMATEL方法中对属性间的影响强度进行判断,确定属性权重更加符合实际决策情况．基于中智集的DEMATEL主观定权法:

(1) 确定直接影响矩阵．根据专家打分法对元素之间的影响强度进行判断,设属性Ci对属性Cj的影响强度为aij=〈Taij(x),Iaij(x),Faij(x)〉,其中当i=j时,aij=0,即直接影响矩阵为:

(2) 利用文中提出的新记分函数式(11),将基于单值中智集的直接影响矩阵A转化为实数矩阵A′；

(3) 根据DEMATEL算法,通过式(4～8)求出各个属性的中心度Gj；

(4) 中心度即表示属性在系统中的相对重要程度,中心度越大,则表示属性在系统中越重要,这与属性权重的意义相同．因而,主观权重公式为:

(12)

3.1.2 客观权重确定

自信息熵提出后,熵成为衡量信息不确定性的重要依据,熵权法的原理是:如果指标间差异越大,则赋予的权重就越大,反之越小[36]．单值中智集熵的计算步骤为:

(1) 对决策矩阵D=[dij]m×n进行标准化,得到R=[rij]m×n．对于效用型指标,对应决策信息不用改变,对于成本型在综合权重中所占的比例,α∈[0,1 ],决策者根据主观意愿可以对α取不同值,以调整主客观权重在综合权重中的占比,对于成本型指标,取其补集,根据文献[12],计算公式如下:

Ac=〈FA(x),1-IA(x),TA(x)〉

(13)

(2) 根据式(3),计算出对应各个属性的中智熵E(xj),其中1≤j≤n；

(3) 根据熵权法得到属性的客观权重:

(14)

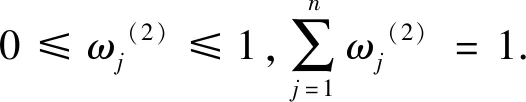
3.1.3 综合权重确定

由于在实际决策中,不同决策环境可能导致主观权重和客观权重的占比不同,因此在综合主客观权重时应强调灵活性．而线性加权法通过调整参数α可灵活确定主客观权重在综合权重中的占比,是一种基于决策者意愿的有效综合定权法．文中定义综合权重公式如下:

ωj=αωj(1)+(1-α)ωj(2)j=1,2,…,n

(15)

3.2 决策流程

步骤如下：

(1) 根据直接影响矩阵A与式(12)确定属性的主观权重ωj(1).

(2) 根据式(13)对决策矩阵D标准化得到矩阵R,根据式(14)得到客观权重ωj(2).

(3) 根据决策问题选择合适的参数α,运用式(15)得到综合权重ωj.

(4)设ω*=max{ω1,ω2,…,ωn},则相对属性权重为:

(16)

(5) 计算属性Cj(j=1,2,…,n)下方案Ai相对于方案Aj的优势度:

φj(Ai,Ak)=

(17)

式中,Sir(α)和Sjr(α)分别为属性Cj下方案Ai和Aj的记分函数；参数θ表示损失的衰减因子,可根据决策者的偏好改变,选取不同的θ将形成不同的前景理论函数，一般θ>0.当0<θ<1时,表示损失的影响将增加,当θ>1时,表示损失的影响将减小．

(6) 计算方案Ai相对于方案的Aj的优势度:

(18)

(7) 计算各方案的综合排序值:

(19)

式中,π(Ai)越大,方案Ai越优．

基于主客观综合定权法的单值中智TODIM决策模型流程图:

图1 决策模型流程Fig.1 Flowchart of decision model

4 案例分析

中小企业是国家发展的中坚力量[37]．2016年世界贸易报告指出中小企业占经合组织企业数的95%以上[38],是稳定我国经济增长的重要保障．在大众创业的背景下,催生了很多中小企业,创业者们或有新颖的理念或有先进的技术,但往往资金匮乏,在企业运行过程中需要外部资金支持,资金来源主要是外部投资人．在决策是否投资某个中小企业项目的过程中,投资人不仅会对中小企业发展潜力作出自己的判断,还会参照专家团队的意见,本部分将中小企业的发展潜力作为主要研究对象进行决策评价．

某投资人确定投资一个中小企业,经过投资人考察有6家企业(A1,A2,A3,A4,A5,A6)具有较高的发展潜力,在投资选择中主要考虑企业的创新能力C1、企业文化C2、企业领导者能力C3和业内竞争情况C44个属性,现需从上述6家企业选出最优的投资对象．经过对6家企业进行分析,投资者对企业Ai的属性Cj进行评价,得到决策矩阵D，如表1．

表1 决策矩阵DTable 1 Decision matrix D

决策者邀请专家团队对属性之间的影响关系作判断,得到直接影响矩阵A，如表2．

表2 直接影响矩阵ATable 2 Matrix A of direct affection

基于主客观综合定权法的单值中智TODIM决策方法过程步骤:

(1) 根据表2的直接影响矩阵A与式(12),求得属性的主观权重:

ω1(1)=0.242,ω2(1)=0.324,ω3(1)=0.168,ω4(1)=0.266

(2) 根据表1的决策矩阵D和式(13)得到标准化决策矩阵R(表3),根据式(14),求得客观权重:

ω1(2)=0.357,ω2(2)=0.142,ω3(2)=0.336,ω4(2)=0.165

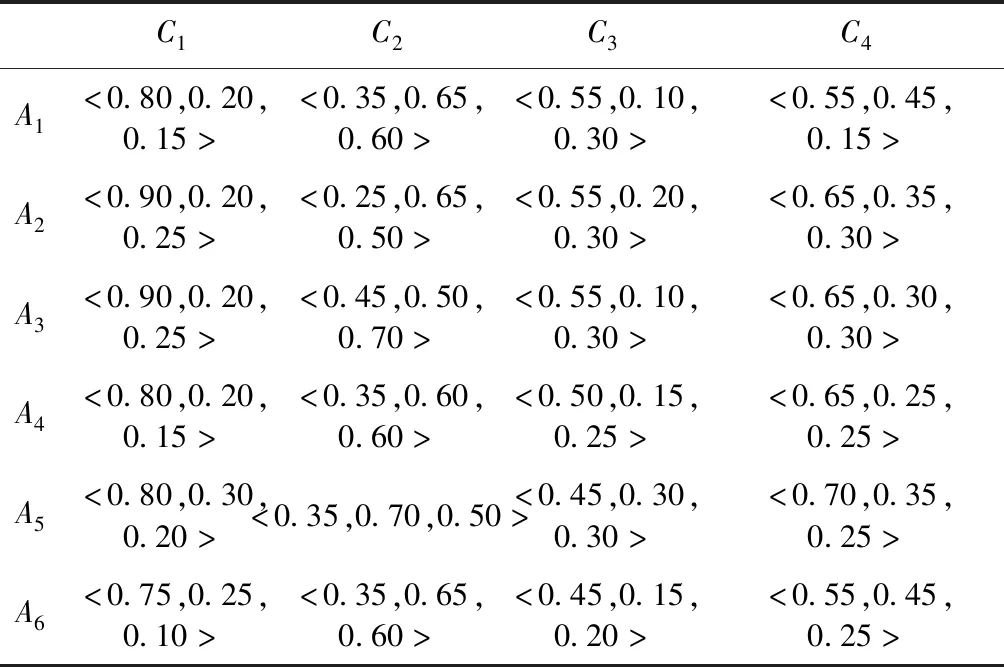
表3 标准化决策矩阵RTable 3 Matrix R of standardized decision

(3) 取α=0.5,根据式(15)线性加权综合定权法,求得综合权重:

ω1=0.300,ω2=0.233,ω3=0.252,ω4=0.215

(4) 根据式(16)与步骤(3)求得的综合权重,得到属性相对权重:

ω1′=1,ω2′=0.777,ω3′=0.840,ω4′=0.717

(5)根据式(17),计算属性Cj的优势度矩阵φj,其中θ=1,求得结果:

(6) 根据式(18),求得方案Ai相对于方案的Aj的优势度:

(7) 根据式(19),求得各方案的综合排序值,并对方案排序:

π(A1)=0.320,π(A2)=0.408,π(A3)=1,

π(A4)=0.861,π(A5)=0,π(A6)=0.594

根据π(Ai)的大小进行排序,求得结果:π(A3)≻π(A4)≻π(A6)≻π(A1)≻π(A2)≻π(A5),即A3≻A4≻A6≻A1≻A2≻A5．

将文中方法与文献[39]所提的TOPSIS方法进行对比分析,运用 TOPSIS方法求得的排序结果如表4.排序结果为:A3≻A1≻A4≻A6≻A2≻A5．可见文中提出的方法与TOPSIS方法求得的最优方案相同,但顺序仍然存在差异,主要是因为文中所使用的TODIM方法考虑了不同投资人的风险偏好,因而决策结果更加符合实际决策情况,而TOPSIS法未考虑人的主观情感因素,所得结果可能与实际有所不同．