钢框架-防屈曲支撑结构抗震性能的振动台试验研究

2020-09-08邵建华刘汶津王展光

江苏科技大学学报(自然科学版) 2020年4期

邵建华,赵超,刘汶津,王展光

(1.江苏科技大学土木工程与建筑学院,镇江 212005)(2.南京大德减震科技有限公司,南京 211103)(3.凯里学院建筑工程学院,凯里 556011)

防屈曲支撑(buckling restrained brace,BRB),又称为屈曲约束支撑．它是一种新型的支撑形式,能为框架或排架结构提供足够的水平抗侧刚度和极限承载力,在强震作用下对建筑结构的消能减震效果得到了业界的广泛认可．

防屈曲支撑常应用于多、高层建筑的抗侧力体系,主要由钢支撑内芯、外包约束构件,以及在上述两者之间所设置的无黏结材料或间隙三部分组成, 具有耗能机制明确、减震效果显著、滞回性能稳定、施工安装方便、易于标准化生产等特点．工作原理是利用外围对内核构件的横向位移进行约束,防止内核发生屈曲,使其能在轴压作用下发生全截面屈服,从而获得拉压对称的受力性能[1]．

近年来,为了研究防屈曲支撑结构的抗震性能,国内外学者对其进行了一系列相关试验和有限元数值分析．文献[2-3]通过位移响应曲线对比分析了分别附加黏滞阻尼器、金属阻尼器以及同时附加两种阻尼器时位移响应之间的关系．文献[4-6]对防屈曲支撑进行了拟静力试验,结果表明:构造合理的防屈曲支撑具有良好的耗能能力,并能在大变形时提供附加刚度;防屈曲支撑连接部位的竖向抗力与水平向抗力相对独立．文献[7-11]对设防屈曲支撑结构与未设支撑结构进行了对比研究,结果表明:防屈曲支撑能有效提高框架抗震性能,其中加设防屈曲支撑的框架结构刚度、承载能力、耗能和阻尼比均显著增大．

为了测试建筑结构中附加防屈曲支撑后在各级不同地震强度作用下的抗震性能,文中采用低屈服点钢材制作内芯板,设计和加工了钢框架-防屈曲支撑结构模型,利用多条地震波对其进行振动台加载试验,研究了BRB结构在不同等级地震波作用下的破坏形式、动力特性、加速度响应、位移、应变等力学性能,并对该结构的抗震性能做出了分析与评价．

1 振动台试验设计方案

振动台模型试验是在实验室进行模拟地震的重要手段,主要从宏观方面研究结构地震破坏机理、破坏模式和薄弱部位,评价结构整体抗震能力并衡量减震和隔震的效果[12]．在进行振动台试验后,通过采集与分析数据,可以精确了解构件在不同地震波强度下的抗震性能及破坏形式．

1.1 试件概况

试验模型采用单跨两层的钢框架-防屈曲支撑结构．考虑到振动台性能参数(如:台面尺寸、锚栓间距、吊装高度、台面最大载重量等)的要求,最终确定对原结构按照1 ∶4缩尺比例进行设计和加工制作模型,并根据Buckingham理论和量纲分析法,得到模型结构主要物理量的相似关系见表1．

表1 模型结构相似关系Table 1 Scaling factors of model structure

该结构模型每层附加2 t的质量块以模拟原结构承受的竖向荷载,模型总质量为4.29 t;平面尺寸为1.2 m×1.2 m,每层层高0.8 m,其中钢柱GZ截面采用H100 mm×100 mm×6 mm×8 mm、框架主梁GL和次梁GCL截面均采用I10工字钢,BRB则由多块钢板焊接而成．其中采用低屈服点钢材LYP100制作防屈曲支撑的内芯板,其他所有构件的材制均采用Q235B钢材．试件的平面图及附加防屈曲支撑榀的立面图如图1;框架梁柱节点采用开坡口的全熔透焊缝连接、柱脚设置加劲肋,以保证各自节点连接的刚性,节点连接三维图如图2．

图1 试件的平面和立面布置(单位:mm)Fig.1 Plan and elevation layouts of specimen (unit: mm)

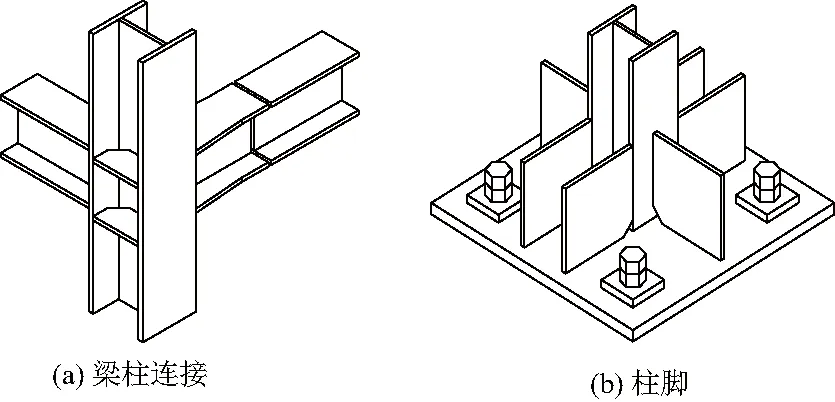
图2 节点连接的三维图Fig.2 3D diagram of joints

1.2 防屈曲支撑构件设计

试验设计的防屈曲支撑仅内芯板与结构的主构件连接,所受的荷载全部由低屈服点钢芯板承担,外部约束钢板仅限制芯板受压屈曲,如图3．

图3 防屈曲支撑构成图Fig.3 Buckling restrained brace

考虑振动台的极限加载能力、试件本身的刚度和承载力,设计的低屈服点钢芯板厚5 mm,防屈曲支撑各板件截面尺寸如图4．通过预先焊接在框架梁、柱上的连接板,使BRB与主框架进行连接;在节点连接处,框架梁腹板设置一定数量等间距的加劲肋,以防止BRB轴向力作用下导致梁腹板发生局部受剪屈曲,如图5．

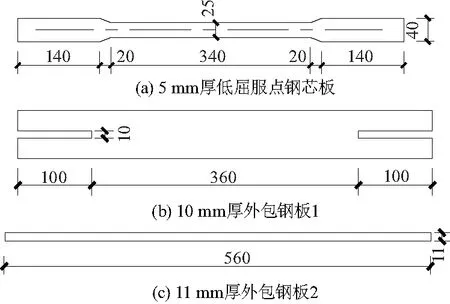
图4 BRB板件详图(单位:mm)Fig.4 Details of BRB plates (unit: mm)

图5 BRB连接节点详图(单位:mm)Fig.5 Detailed connection of BRB (unit: mm)

1.3 材性试验

为了测量钢材的屈服强度fy、抗拉强度fu、弹性模量E、伸长率δ、屈强比等力学性能参数指标,需对试件的钢材进行材性试验．钢材拉伸试验所需材料均从母材中切取,将材性拉伸试件设计为板状,低屈服点钢LYP100材性拉伸试件共3个．

在拉伸试验过程中,低屈服点钢拉伸试件从开始加载弹性到屈服再进入强化直至颈缩断裂阶段,钢材被拉伸得很长,断裂后的截面面积收缩得很小,且断口不平整,断口呈现锯齿状,表现出非常优越的延性性能．拉伸试验断裂后,3个低屈服点钢材性试件如图6．

图6 试件断裂Fig.6 Specimen fracture

低屈服点钢LYP100与普通钢Q235材性拉伸试验的材料力学性能参数如表2．

表2 材性试验结果Table 2 Results of material test

由表2可知,低屈服点钢LYP100的屈服强度约为Q235钢材的0.41倍,抗拉强度约为Q235钢材的0.64倍,屈强比约为Q235钢材的0.63倍,但伸长率却将近是Q235钢材的1.36倍．

1.4 试件制作与安装

钢框架-防屈曲支撑结构试验的加载设备采用台面尺寸为4 m×6 m的振动台,并进行单向多条水平地震波加载,振动台性能参数如表3．

表3 振动台性能参数Table 3 Performance parameters of shaking table

试件的所有构件都在工厂加工制作,框架梁柱节点均采用全熔透的焊接连接．钢柱脚焊接一块厚20 mm的底板,并设置φ37 mm的螺栓孔,孔间距300 mm,以便与振动台台面进行螺栓连接和固定．在每层楼面钢梁上点焊一块5 mm厚的钢板,以放置由橡胶隔震支座和圆形钢板片组成的附加质量块．每层楼面钢板的中心开孔,质量块吊装就位后用螺栓将其固定在钢板上,以保证其在试验过程中不会出现滑移．试件制作完成后,吊装运送至结构实验室,如图7．

图7 试件安装Fig.7 Installed specimen

1.5 测试内容和测点布置

通过试验测量的应变、位移响应来分析和评价钢框架-防屈曲支撑结构在不同地震波各地震强度等级作用下的抗震性能指标．应变测量采用电阻应变片,选用江苏泰斯特电子设备制造有限公司生产的TST3827E动静态信号测试分析系统．位移测量采用量程为±50 mm的YHD型位移传感器和量程为±250 mm的TST顶杆式位移计,对应的数据采集系统分别采用DH3820-Net高速静态应变测试系统和TST3000动态测试分析系统．

钢框架-防屈曲支撑试件的测点布置包括应变片布置和位移计布置．每个框架梁柱构件各布置4个应变测点,即柱两侧翼缘的顶端和底端各设置一个应变片,梁两端的上下翼缘各设置一个应变片;在每个BRB上各布置两个应变片．试件共计布置64个应变测点,在框架每层梁柱节点连接处各布置一个位移计,测点布置如图8．

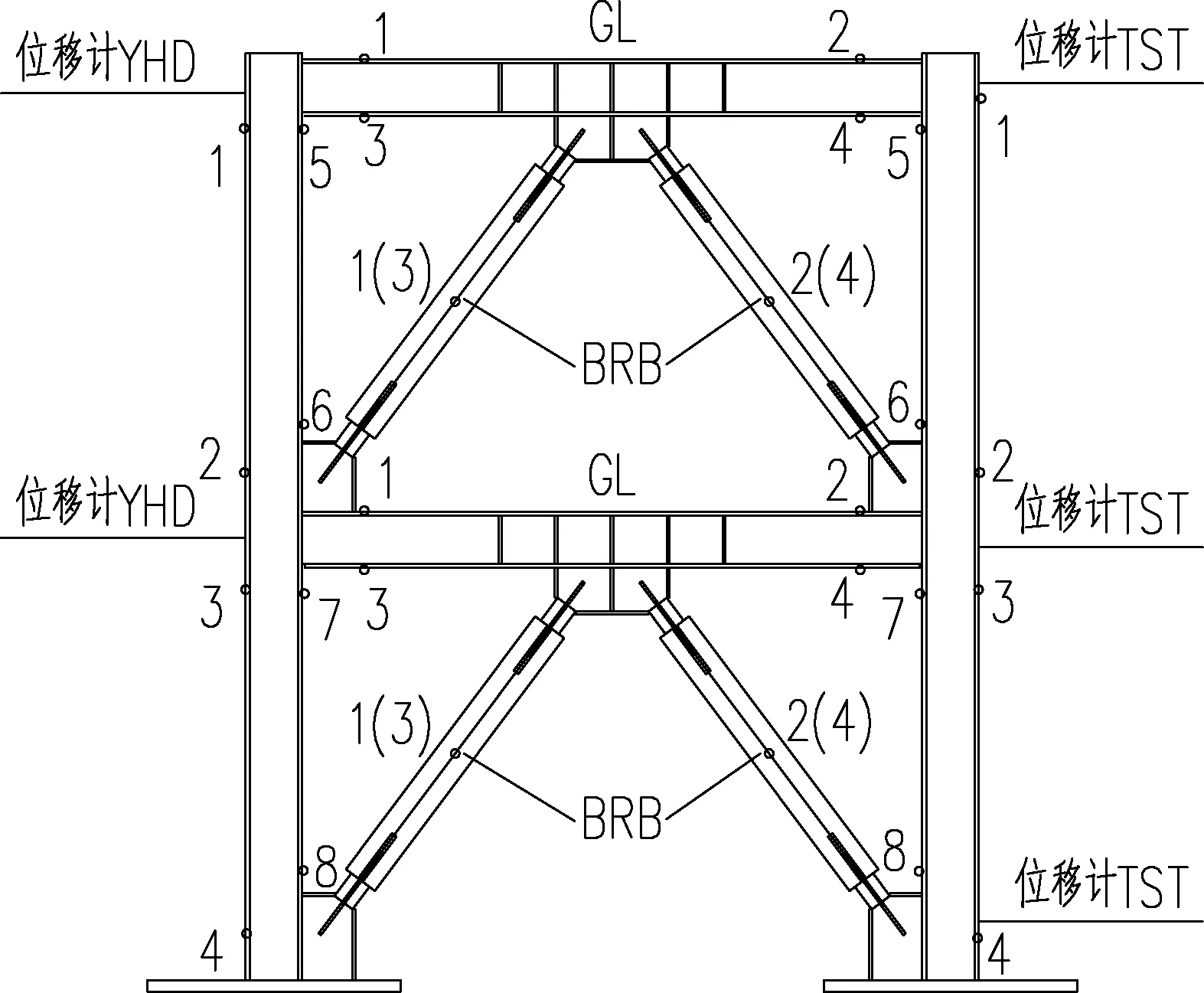
图8 测点布置Fig.8 Layout of measurement points

1.6 加载方案

振动台试验一般要求选用3条以上不同的地震波,并需要考虑地震波的三要素:地震波的有效峰值、持续时间和频谱特性,选择适应于地震烈度、场地类型、地震分组的地震动．本次试验筛选出符合结构动力特性的El Centro波、Kobe波、Taft波作为振动台台面输入的3条地震波,如图9．

图9 加载的地震波Fig.9 Loading earthquake waves

在振动台试验中,加速度相似比Sa是施加地震波动力荷载的主要控制参数,考虑到振动台噪声、台面承载力、试件截面尺寸等因素,以及根据以往试验经验,试验采用的加速度相似比确定为Sa=1.8．

本试验方案按照抗震设防烈度8度设计试件,根据《建筑抗震设计规范》(GB 50011-2010)[13],即试件在多遇地震(小震)、设防地震(中震)和罕遇地震(大震)下的加速度峰值分别为0.126、0.36和0.72g．为了研究防屈曲支撑构件在不同地震强度等级作用下的耗能减震能力,试验加载时将3条地震波的峰值加速度进行调幅,按照每间隔0.1g,设定从0.1g由小到大逐级增加到1.0g,共分为10个等级,分别对应工况1至工况10．试验之前以及每级地震波加载之前都用白噪声对结构模型进行扫频,具体的试验加载工况如表4．

表4 试验加载工况Table 4 Loading cases of test

利用试验实测数据进行试件的结构性能分析时,以加载的峰值加速度值略大于各地震水准的峰值加速度作为该水准的抗震性能评判,即小震、中震和大震分别对应于加载工况2(峰值加速度为0.2g)、工况4(0.4g)和工况8(0.8g)．

2 试验现象

钢框架-防屈曲支撑结构在整个振动台加载试验过程中,各构件无明显破坏现象,显示出良好的抗震性能,试验现象如图10．

在地震波峰值加速度为工况1至工况2(小震)作用时,构件或部件间的相对晃动不明显,没有声响,结构整体保持完好．在工况3至工况4(中震)地震波激励时，二层的质量块有轻微的晃动和少许的声响,并伴随有少量灰尘,但结构整体仍保持完好,见图10(a)．在工况5至工况6作用时,二层质量块有明显地晃动,并发出声响,柱脚焊缝处的锈斑掉落明显,见图10(b)．在工况7至工况8(大震)作用下,二层的质量块晃动更加明显,且发出“哐哐”的声响,此时一层的质量块也开始有明显地晃动,锈斑掉落现象更加明显,框架梁柱上均出现不同程度的微小拉裂痕,见图10(c)．在工况9至工况10作用下,二层的质量块晃动很大,并发出巨大声响,一层的质量块也晃动明显,灰尘抖落严重,有部分架设的位移计、应变连接线被震落,见图10(d)．

图10 试验现象Fig.10 Test phenomena

3 试验结果及分析

3.1 动力特性

在各级地震波加载工况之前,先对结构进行白噪声扫频,得到结构的自振频率,然后采用半功率带宽法[14]计算结构的阻尼比．白噪声激励下试件的动力特性如表5．

表5 试件的自振频率和阻尼比Table 5 Natural frequency and damping ratio of specimen

由表5可知,钢框架-防屈曲支撑试件的初始基本自振频率为23.12 Hz,初始阻尼比为2.78%．随着试验加载的地震波峰值加速度增大,结构的自振频率逐渐降低,周期变长,且阻尼比越来越大．这是由于柱脚都是通过高强螺栓与振动台面连接,而且所有的附加质量块均通过螺栓杆固定在框架楼层．随着输入峰值加速度的增大,螺栓会产生松动而引起构件间的相互摩擦,使得结构的阻尼比增加．

(1)

式中:k0、k分别为结构试验时的初始刚度和某一工况下加载完成时的刚度;f0、f分别为结构的初始自振频率和某一工况加载结束时的实测频率．

由式(1)得到试件的刚度退化率如图11．由图可知:从整体上看,随着峰值加速度的增加,刚度退化率下降越来越显著．在整个试验过程中,结构的刚度退化率最大值为5.4%,退化程度并不太大,说明试件在试验结束时还具有较强的水平抗侧刚度．试件在8度小震和中震作用下的刚度退化率仅分别为0.33%和1.0%;而在大震作用下刚度的退化较之前更为明显,为3.55%．

图11 结构的刚度退化Fig.11 Stiffness degradation of the specimen

3.2 加速度响应

振动台试验常用加速度放大系数来表征结构模型在不同地震工况下的动力放大特性．钢框架-防屈曲支撑结构模型在3条不同加载地震波作用下小震、中震和大震时的加速度放大系数如图12．

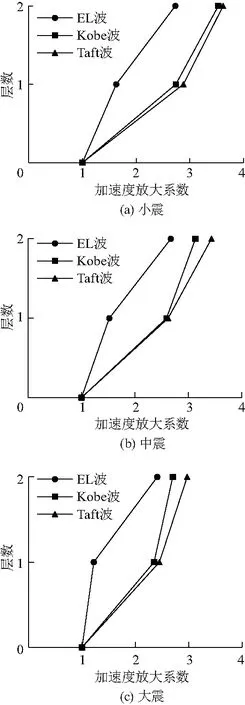
图12 试件的加速度放大系数Fig.12 Acceleration amplification factor of the specimen

由图12可知,结构第二层的加速度放大系数要大于第一层;在相同的地震强度等级作用下,不同的地震波对结构的动力放大效应有着明显的区别,EL Centro波的地震作用要优于另外两条地震波;对于同一种地震波,结构的加速度放大系数随着地震强度的增大而减小,在Taft波小震、中震和大震作用下二层的加速度放大系数分别为3.62、3.43和2.97．这是由于地震作用越大,结构的响应越剧烈,各部件之间会产生摩擦和相对运动、螺栓松动等现象,从而减轻结构的动力放大效应．因此,结构的加速度放大系数与地震作用强度、选择的地震波、结构层数等因素都有关系．

3.3 位移响应

层间位移是抗震规范中的一个重要设计指标,“大震不倒”的抗震设计目标就是通过结构层间位移来控制．通过分析试件各层测点布置的位移传感器所采集的数据,可得到结构各层的最大位移及最大层间位移角,其中试件在3种不同地震波各加载工况下每层的最大位移包络如图13．

图13 试件的最大位移包络Fig.13 Maximum displacement envelope of the specimen

由图13可知,结构的最大位移随着峰值加速度的增加而增大,呈上升趋势．在中震(工况4)作用之前,结构各层的最大位移值都较小,位移增加较缓慢,且变化趋势呈近似直线,此时结构保持弹性状态．而在中震至大震(工况8)作用时,结构的最大位移明显增加,且位移不再按原来直线变化,增大趋势更加显著,这是由于此时结构出现了一定的损伤,水平抗侧刚度下降相对较多,导致位移变化更大．

根据各层测点所测量的位移时程,得到试件在不同地震波各加载强度等级下的最大层间位移角,如表6．由表可知,在小震(工况2)下,3条地震波作用时结构的最大层间位移角平均值为1/3 000,远小于《建筑抗震设计规范》中规定的弹性层间位移角限值1/250;在大震(工况8)下,结构的最大层间位移角平均值为1/314,小于弹塑性层间位移角限值1/50．以上表明,钢框架-防屈曲支撑结构具有较高的水平抗侧刚度和良好的抗震性能,完全能满足结构抗震设计中的性能指标要求．

为了对比分析不同地震波对结构抗震性能的影响,绘制出3条地震波作用下二层最大层间位移角的变化规律,如图14．

图14 二层的层间位移角Fig.14 Inter-story drift ratio at the second floor

由图可知,在峰值加速度为0.1g～0.4g时,3条地震波下结构的层间位移角变化大致相同,呈线性变化,且数值无较大差异;在0.4g～0.6g时,同等地震强度下Kobe波的最大层间位移角响应远大于El Centro波和Taft波,最大值达到1/400;在0.6g～0.9g时,El Centro波下的最大层间位移角变化呈直线上升状态,而另两条地震波下层间位移角的增加幅度则相对缓慢,试验结束时El Centro波下的层间位移角最大,为1/263．

表6 试件的最大层间位移角Table 6 Maximum inter-story drift ratio of the specimen

3.4 应变响应

通过布置在钢框架-防屈曲支撑试件各层测点上的应变片,可得到实测的应变时程数据．试件柱底处在3条地震波小震(工况2)和大震(工况8)作用下的应变时程曲线如图15．由图可知,加载的峰值加速度越大,柱底的应变响应值越大;不同地震波对结构产生的最大应变响应具有差异性;在同一地震波不同强度作用下,应变响应时程曲线形状并不相似,曲线并不是根据峰值加速度的比值关系直接地线性放大或缩小．

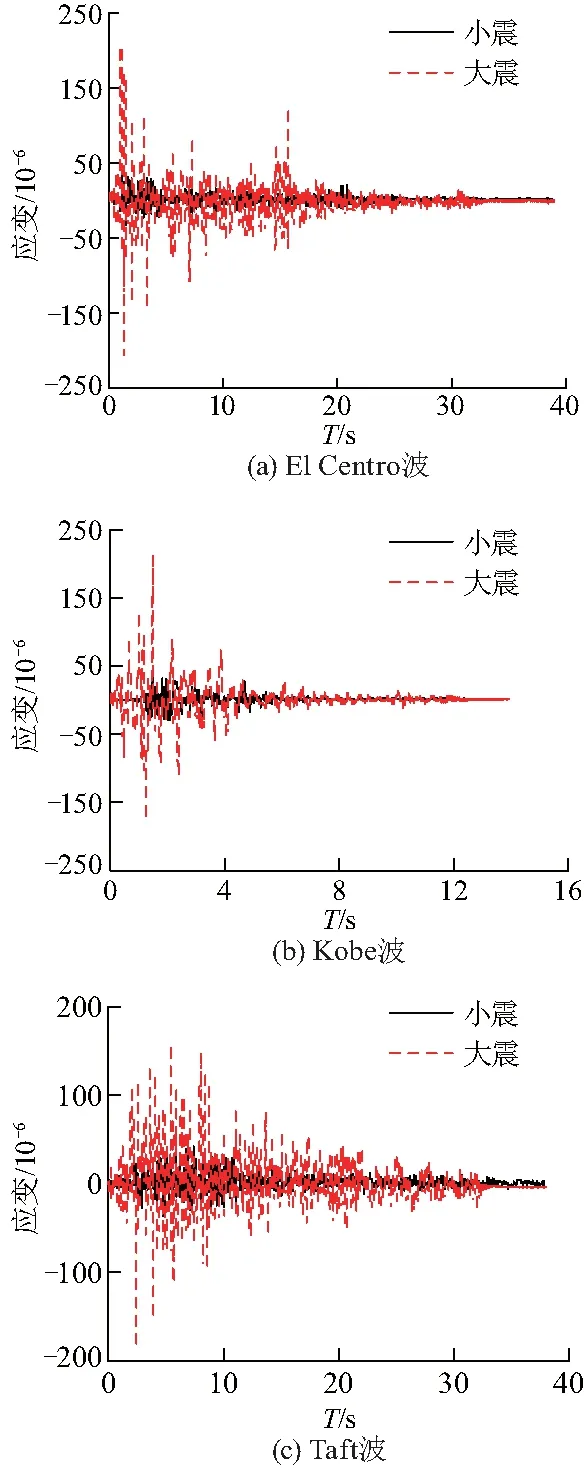
图15 小震和大震下的柱底应变Fig.15 Strain at the column base under frequent earthquake and rare earthquake

为了研究附加防屈曲支撑之后对主结构的抗震保护和强度状态,在结构框架梁和柱不同位置上布置了大量的应变片,得到了主结构在不同地震波加载作用下的应变,以El Centro波为例,其应变变化见图16．由图可知,随着地震峰值加速度增加,结构梁和柱各测点的应变值逐渐增大,在工况0.5g前,所测位置处的应变值都较小,且呈线性变化,结构处于弹性工作阶段;而在工况0.6g后,此时结构刚度退化明显,各测点的应变值都显著增加,且呈非线性变化．框架梁上、下翼缘的最大拉或压应变值在地震强度等级较小时,两者相差不大,但加载等级变大后,两者差别很明显,且下翼缘的应变值比上翼缘大．同一工况下,一层柱的应变值要大于二层柱,所以在设计时需要对底层柱进行构件截面加强,以避免底层柱过早地出现塑性铰而发生破坏．