基于滤波残差多方向差分的数字图像取证
2020-09-07黄荣梅王婷婷
黄荣梅,王婷婷
(四川职业技术学院 计算机科学系,四川 遂宁 629000)
0 引言
近年来,数字图像被广泛应用在不同领域,同时有非常重要的作用,在信息采集与发布领域,数字图像有很大的优势,为人们的工作学习提供重要信息[1,2]。特别是在网络中,数字图像作为多媒体信息被广泛应用,但与此同时,也出现了一些不足。数字图像可提高信息资源的质量,然而容易被篡改,利用常用的图像编辑软件与图像处理装置即可进行,通常在数字图像中无法发现篡改痕迹,无法有效判断图像的真伪[3,4]。通过不正当方式对数字图像进行篡改,会对社会正常发展秩序产生不好的影响。恰恰因为无法判断数字图像中是否有编辑与篡改的痕迹,其真实性往往很难确定,对图像的取证有很大难度[5]。
采用智能取证技术能够实现图像防伪,通过先进技术完成对数字图像的取证,找到数字图像被编辑与篡改的痕迹,真实可靠的数字图像可被当作关键证据信息,很好地解决数字图像取证面临的问题[6,7]。
当前有关数字图像取证的研究大部分是检测几何变换、对比度增强、JPEG压缩、中值滤波等[8]。中值滤波为常见的图像滤波器,这主要是因为其具有很好的平滑滤波性,可保持边缘特征,攻击者可以把中值滤波技术应用于反取证技术中,令中值滤波检测取证被广泛关注[9]。
现阶段已有的中值滤波取证方法更多针对没有被压缩图像是否经中值滤波处理,部分方法对有损压缩或较小图像块的鲁棒性较差。为此,提出一种基于滤波残差多方向差分的数字图像取证方法。经验证,所提方法可有效检测不同种类空域滤波操作,对有损图像压缩鲁棒性高。
1 数字图像滤波残差分析
滤波处理是常用的数字图像编辑方式,其基本思想为对数字图像局部邻近像素值进行加权操作从而完成数字图像处理,滤波过程可通过下式进行描述:
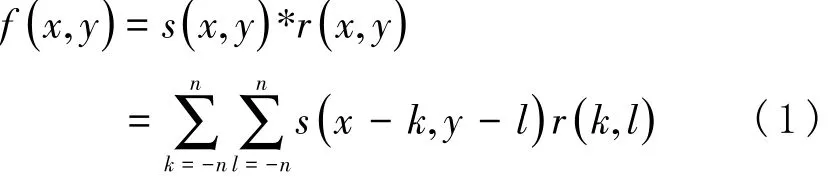
式中,f(x ,y)用于描述滤波数字图像像素值,s(x ,y)用于描述原始数字图像像素值,r(x ,y)用于描述空域平滑滤波模板,*代表卷积操作,n代表滤波器窗口大小。
常见的滤波模板包括均值滤波模板、高斯滤波模板以及中值滤波模板,前两种滤波模板是线性滤波器,中值滤波模板为非线性滤波器,通过像素邻域中值对该像素值进行替代,降噪效果优,模糊程度低[10,11]。
在频域中能够有效反映出滤波器特性,所以本节在频域中对滤波数字图像的特征进行分析,上式频域描述如下:
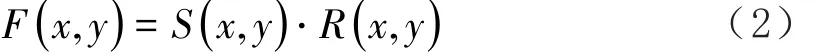
式中,F(x ,y)、S(x ,y)依次用于描述滤波数字图像频谱与原始数字图像频谱,R(x ,y)用于描述滤波处理的频率响应。
若滤波数字图像再经滤波器Rd(i , j)处理,那么其滤波残差可描述如下:
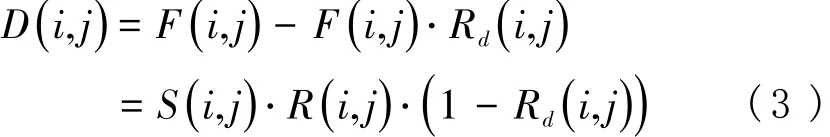
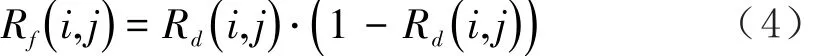
假设复合滤波器频率响应有自己独特的性质,那么被滤波处理后的数字图像即可和原始数字图像区分,所以选择合理的特征提取域为实现鲁棒数字图像取证的重要环节。数字图像多样性以及后处理操作对数字图像取证性能和鲁棒性会产生很大影响,例如JPEG压缩等处理[12]。由于数字图像空域高频分量内容信息相对较少,同时受后处理的影响相对较小,因此可被当成特征提取域,从而降低不利因素产生的影响,本节将滤波残差作为特征提取域。
残差滤波存在下述特性:
(1)滤波残差仅含有较少的数字图像内容,分析图1(b)和图 1(c)可知,原始数字图像滤波残差和滤波数字图像的滤波残差绝大多数是黑色,说明部分滤波残差值为0或趋近于0。
(2)滤波残差能够有效体现原始数字图像和滤波数字图像之间的统计差异。分析图1(b)和图1(c)可知,滤波数字图像滤波残差0像素值明显更多,表明滤波残差能够反映出模糊滤波的低通性质。除此之外,分析数字图像的边缘细节可以看出,滤波数字图像滤波残差过渡较为平缓,这主要是由于模糊滤波令数字图像更加平滑。

图1 原始数字图像和滤波残差
为了提高数字图像取证的准确性,下面依据滤波残差提取小波空间特征谱熵以及自回归系数特征,小波空间特征谱熵用于采集模糊滤波处理在数字图像滤波残差纹理部分遗留的痕迹,自回归系数特征用于对滤波残差进行多方向差分特征提取。
2 数字图像滤波残差特征提取
2.1滤波残差小波空间特征谱熵提取
模糊滤波是一种低通滤波方式,会造成滤波前后数字图像在高频部分有明显的不同[13]。小波空间特征谱熵能够有效识别数字图像滤波残差纹理,本节通过小波空间特征谱熵获取模糊滤波处理在滤波残差纹理区域留下的痕迹。
小波分析理论近年来逐渐发展,其可被看做是一个数学显微镜,能够放大、缩小以及平移。利用检查不同放大倍数的改变情况对信号动态特征进行分析,所以小波分析被应用在较多领域,有很好的可行性。通常数字图像特征提取均是对区域特征或时域特征进行提取,在数字图像性质与拍摄环境相对一致的情况下,上述特征无法有效区分图像。为此,依据小波变换在时频域中联合,提取小波空间特征谱熵,对数字图像滤波残差纹理区域留下的痕迹进行提取分析。
小波变换前后,有限能量函数的能量是守恒的,也就是:

在上述分析中,Wf( )a,b用于描述小波变换幅值,Cv用于描述小波函数的允许条件,P()a用于描述尺度是a的情况下函数e()t的能量值。
小波变换实际上就是把一维信号映射至二维小波空间中,用下述矩阵描述二维小波空间小波能量分布矩阵:

将W当成模式矩阵,完成对其的奇异值分解处理,得到的结果用σi进行描述。那么奇异值谱即为对原始数字图像在时频域中的分割,所以时频域中数字图像小波空间特征谱熵可描述如下:v

小波空间特征谱熵可有效体现数字图像滤波残差能量在时频域中的分布状态,从而体现数字图像纹理特征,数字图像滤波残差不同纹理特征对应的小波空间特征谱熵存在很大差异,利用比较数字图像滤波残差小波空间特征谱熵即可完成对其纹理特征的有效提取。
2.2滤波残差多方向差值自回归系数特征
数字水印与多媒体取证为常用的多媒体安全技术,均值滤波、高斯低通滤波以及中值滤波都属于局部邻域操作,一定会对想理你像素局部统计关系产生一定的影响,采用小波空间特征谱熵对邻域较大的局部统计关系进行描述,在很大程度上会导致特征维数过大,本节通过自回归系数对滤波残差多方向差值特征进行提取,从而描述数字图像的局部统计关系[14],通过自回归系数得到的特征利用Lar进行描述。
在对滤波残差多方向差值特征进行提取的过程中,自回归系数依次按水平与垂直两个方向进行提取,二者的均值就是Lar。
针对水平方向提取自回归系数的过程分析如下:逐行把滤波残差数字图像转变成一维序列,然后把序列输入自回归模型中对自回归系数进行计算。
自回归模型可通过下式进行描述:
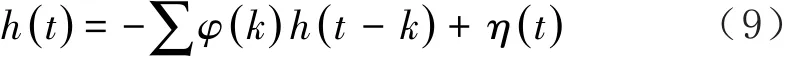
对滤波残差数字图像进行转置处理,利用相同方式对垂直方向自回归系数进行计算,得到的水平方向与垂直方向自回归系数的均值即为滤波残差多方向差分自回归系数Lar。
本研究最终提取特征由小波空间特征谱熵与自回归系数特征组成,也就是
3 利用分类器实现数字图像取证
本节分类器选择支持向量机,支持向量集是一种利用统计学理论实现的分类器,一般被应用在模式识别上。其基本原理为利用已经选择好的非线性映射,也就是核函数把输入向量映射至高维特征空间,同时在该空间中建立最优分类超平面。本节核函数选择高斯函数:
利用多次交叉检验得到最优和参数。通过支持向量机对多分类问题进行解决之前,首先需把多分类问题转变成多重二元分类问题。通常选择一对多策略,也就是在任意两种样本间建立支持向量机分类器,在对某未知样本进行分类的过程中,得票最多的就是该样本的所属类别。
利用分类器实现数字图像取证的基本过程如下:
(1)得到数字图像滤波残差。
(2)对滤波残差小波空间特征谱熵进行提取,通过自回归系数得到滤波残差多方向差分特征,将两种特征构成总特征。
(4)利用分类器对数字图像进行分类处理,检测数字图像是否经篡改处理,从而实现数字图像取证。
4 实验结果及分析
实验将文献[5]方法和文献[8]方法作为对比进行分析,验证本文方法对数字图像取证的有效性。
实验在非压缩数字图像数据库中进行相关实验分析,该数据库中一共包含1800幅数字图像,在进行实验时随机从数据库中选择150幅数字图像。实验过程中,对数字图像进行滤波篡改处理,同时对篡改数字图像添加信号处理攻击,攻击处理主要有加入噪声、对数字图像进行JPEG压缩处理以及对数字图像进行高斯模糊处理。
实验衡量指标为整个篡改数字图像像素点的准确检测率以及错误检测率,两个衡量指标的计算公式分别如下:

其中,I1用于描述处理部分,O1用于描述篡改部分,I2与O2依次用于描述检测到的处理部分与篡改部分。
表1描述的是采用本文方法、文献[5]方法以及文献[8]方法对数字图像进行取证处理时,准确检测率与错误检测率的比较结果,其中的值均为150幅图像的处理均值。
由表1中得到的数据可知,和JPEG压缩攻击比较,噪声攻击与高斯模糊攻击对本文方法的检测率没有很大的影响,准确检测率均超过99%。而在JPEG质量因子逐渐升高的情况下,本文方法准确检测率提升,错误检测率减少,在JPEG质量因子是30的情况下,本文方法准确检测率也可达到91%,错误检测率较低,在实际应用中,JPEG质量因子一般取50,所以采用本文方法可很好地处理JPEG压缩攻击。准确检测率均更高,有很大的优势。
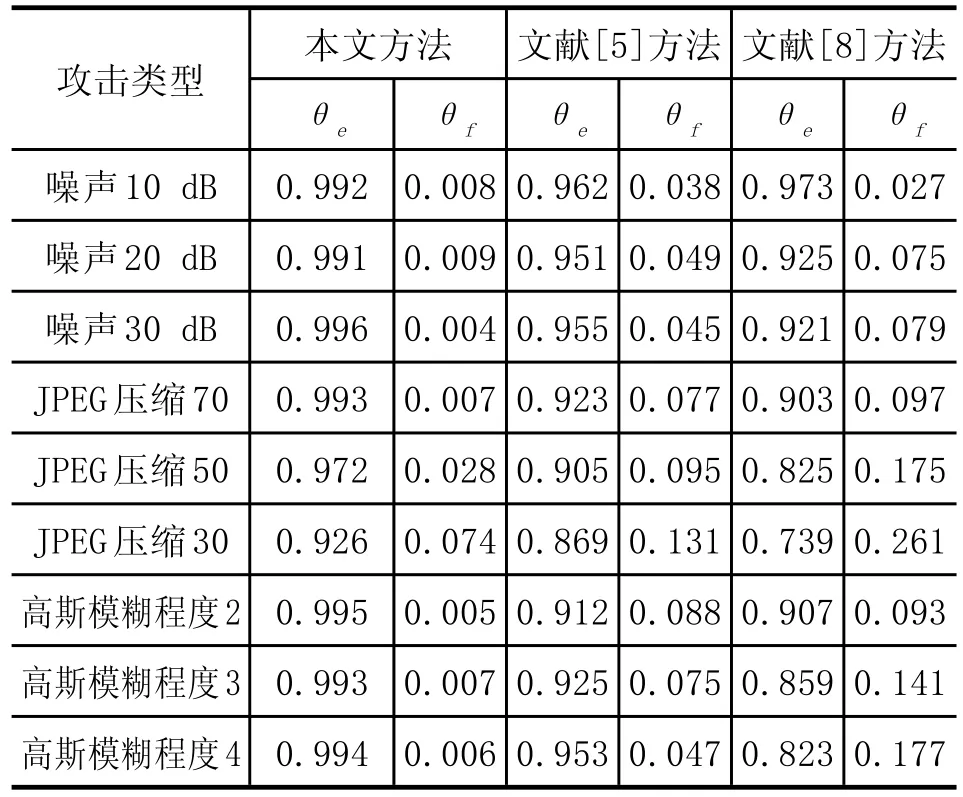
表1 三种方法检测结果比较
5 结论
本文提出一种基于滤波残差多方向差分数字图像取证方法。对数字图像进行滤波残差分析,对滤波残差小波空间特征谱熵进行提取,通过自回归系数得到滤波残差多方向差分特征,将两种特征构成总特征。依据提取的总特征,通过支持向量机进行检测,实现数字图像取证。实验结果表明,所提方法有很高的准确检测率,可检测出有多个攻击的篡改图,有较高的性能,实用性强。
