基于SPH 无网格法的纺锤形桩靴连续贯入过程模拟

孟 翔，高路恒，吴 浩，Atangana Njock Pierre Guy

(1.江苏工程职业技术学院 建筑工程学院，江苏 南通 226001；2.上海交通大学 船舶海洋与建筑工程学院，上海200240)

纺锤形桩靴是岩土工程、港口、海岸及海洋工程等领域中常见的深基础形式，为了承担上部结构自重及工作载荷，保证平台的安全使用，桩靴底部一般设计成扩大的倒圆锥形或圆盘形，桩靴底部直径一般为10～20 m，贯入土体中深度可达数倍直径以上[1-3]。对桩靴贯入过程进行数值模拟对于提高设计水平、保证施工安全具有重大意义。然而，由于桩靴特殊的几何形态，其贯入过程常伴随极大的土体变形及超孔隙水压力的变化，采用传统的网格类数值方法（如FEM）时会遭遇严重的网格畸变而导致计算失败。因此，早期Hossain[4]，Tho[5]及Zhou[6]等的研究均假定桩靴预先埋置于一定深度，而后基于拟定的初始应力场进行小变形分析。然而，Hossain 等[4]已经证明，这种简化后的小变形分析结果与连续贯入大变形分析以及室内离心机试验结果存在很大误差。近年来，国内外学者尝试采用CEL，ALE，RITSS 等大变形有限元分析方法（LDFE）对桩靴的连续贯入过程进行模拟[4,7-9]。从工程应用角度而言，LDFE 的使用极大地促进了人们对桩靴贯入过程中物理现象的理解和问题的解决，但以往LDFE 研究均未能考虑到真实贯入过程中土、水两相耦合作用，并且频繁地进行网格重分和物理量映射也会造成计算精度损失[10]。

光滑粒子流体动力学（SPH），作为一种完全的拉格朗日无网格方法，由于其无网格属性、粒子属性及自适应性，越来越多地被用于求解各类大变形问题。Maeda 等[11]、Bui 等[12]最早建立土、水耦合SPH 方程并用于模拟射流破土问题。其后，Huang 等[13]在此基础上将土、水耦合SPH 方程推广到非饱和土即气-液-固三相耦合作用模型，并对渗流破坏问题进行研究。Wu 等[14]在SPH 框架下首次建立了土-水-结构耦合SPH 算法并应用于贯入问题的模拟。本文采用Wu 等建立的土-水-结构耦合SPH 算法对纺锤形桩靴连续贯入过程进行数值模拟，在考虑土体大变形以及土-水-桩靴三者耦合作用条件下研究桩靴贯入阻力及桩靴底部超孔隙水压力的变化规律。

1 基本理论

1.1 SPH 的基本原理

SPH 本质上是一种插值方法，其主要思想是借助于有限数量的携带场变量和材料属性的粒子，离散化偏微分方程组（PDEs）所定义的问题域，粒子与粒子之间无固定联系。场函数及其梯度首先通过光滑函数转化为积分近似表达式，而后通过对支持域内相邻粒子插值转化为粒子近似表达式，从而将PDEs 转化为一系列常微分方程（ODEs）进行求解[10]。场函数及其梯度的最终粒子近似式[10]为：

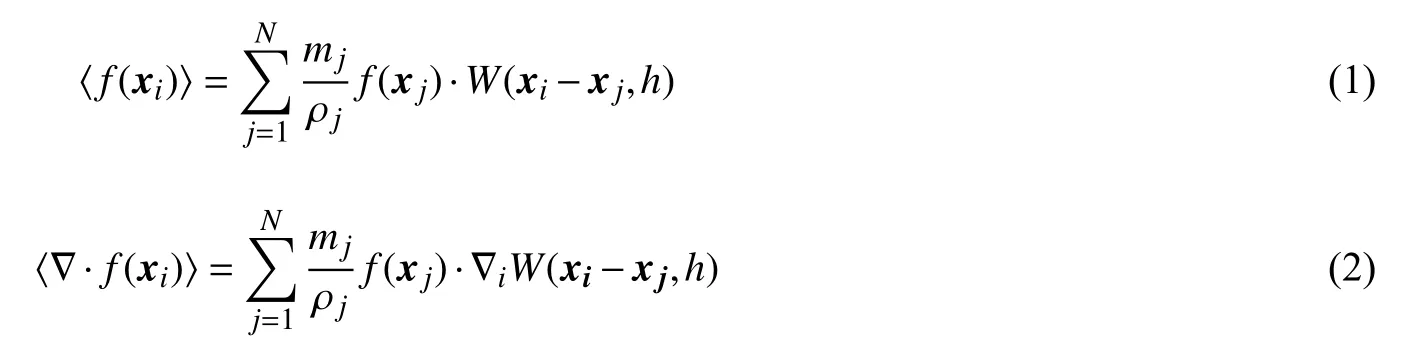
式中：f 为三维空间坐标向量x 的函数；i，j 为粒子的标识；mj为粒子质量；ρj为粒子密度；N 为相邻粒子总数；W 为光滑函数；h 为光滑长度。本文采用Wendland 型[15]光滑函数，形式如下：

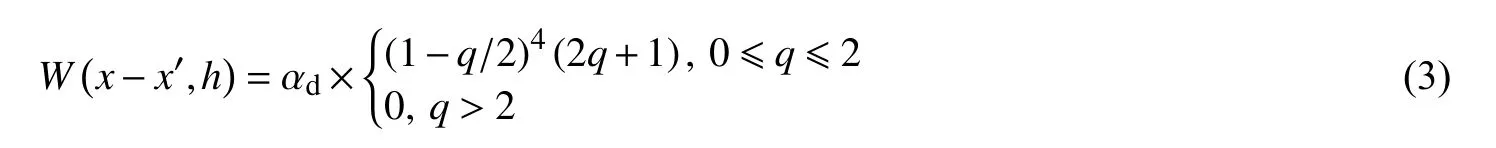
式中：αd为正则化参数，对于二维问题取值7/（4πh2）；q 是点x 和x'之间的相对距离，q=|x-x'|/h。

1.2 土-水混合物控制方程及SPH 离散化

土-水混合物的控制方程由土、水两相各自的质量守恒方程（4），（5）及动量守恒方程（6），（7）构成[14]：

式中：k 为土体的渗透系数。

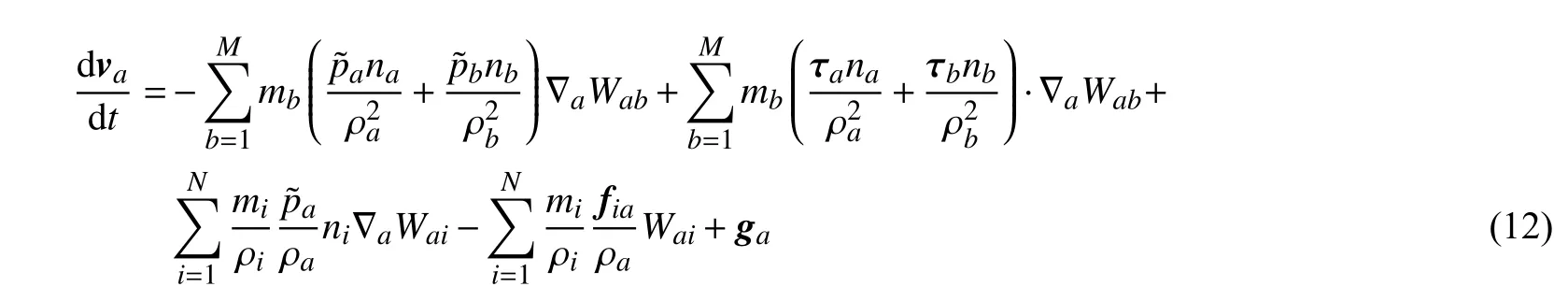
式中：下标i，j 和a，b 分别用来标识土体和孔隙水；υji=υj-υi，即粒子j，i 的速度差；υab=υa-υb；土-水两相之间的黏滞性拖拽力fia的SPH 粒子近似式为[14]：

方程组（9）～（12）含有未知量：孔隙率n，土体速度νs，水的速度νf，水的密度ρf，土体有效应力σ'，孔隙水压力及黏性力。σ'由土体的本构方程求得，本文假定土体为理想弹塑性材料，采用Drucker-Prager 屈服准则和非相关联的流动法则；假定孔隙水为弱可压缩性牛顿流体，由孔隙水的状态方程求得；由动力黏滞系数和剪应变率求得。土、水两相的粒子与桩靴之间的接触力采用摩擦滑移算法[14]计算。

2 桩靴贯入过程模拟及结果分析

采用上述SPH 算法分别对轴对称条件下砂土和黏土中的桩靴贯入过程进行模拟，研究土体存在极大变形情况下贯入阻力以及孔隙水压力的变化规律。如图1 所示，桩靴为刚体并以恒定速度0.1 m/s向下贯入土中，与混合物之间采用摩擦滑移接触。模型左侧为对称轴边界，采用镜像虚粒子模拟。模型右侧和底部分别采用两排、四排虚粒子进行模拟。

2.1 砂土中贯入模拟及贯入阻力分析

模拟中密、密实砂土两种工况，模型参数见表1。其中cf为孔隙水中声音传播速度；υ 为土体的泊松比；E 为杨氏模量；c 为黏聚力；ϕ，ψ 分别为土体内摩擦角和剪胀角；μ 为液相及水的动力黏滞系数；ID为土体相对密实度；其他参数物理意义同上。Qiu 等[8]在研究桩靴基础穿透破坏问题中，采用CEL 对桩靴基础的连续贯入过程进行模拟。为便于对比分析，采用的模型与之保持一致，最大贯入深度为3.6 m。

图1 桩靴贯入模型Fig.1 Schematic diagram of the simulation arrangement

表1 土体、水的物理参数以及模型几何尺寸Tab.1 Dimensions and parameters for soil and water phases

图2 为工况1 中密砂土中的桩靴贯入过程。初始状态下，桩靴底部完全浸没在自由液面以下、土体表面以上。贯入深度d=2.0 m 时，桩靴底部土体向下、向外发生位移并发生隆起变形，周围土体和水的SPH 粒子遵循各自控制方程运动，位置发生错动。d=3.6 m 时，桩靴顶部形成深度约为3.0 m 的柱状孔，未发生土体回淤现象。可以看出，计算过程中水面始终未发生变化，与直观认识一致。采用SPH 可以很好地模拟土、水混合物大变形过程而不会发生网格畸变等问题。

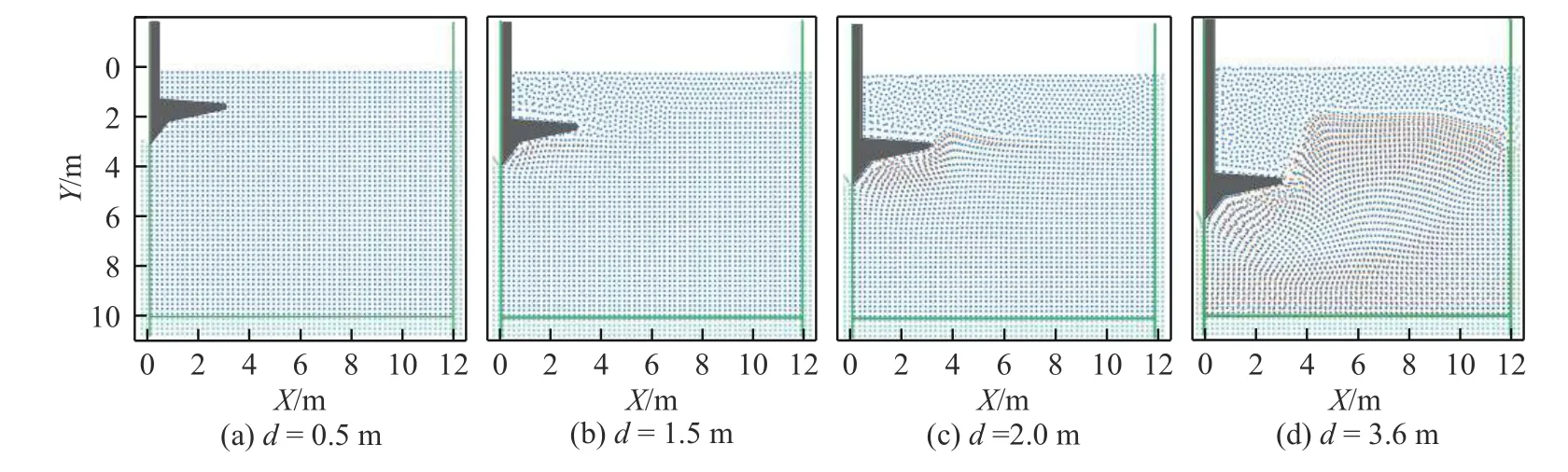
图2 桩靴在砂土（中密）中贯入过程Fig.2 Penetration process of spudcan into medium dense sand

图3 （a）和（b）分别为桩靴在中密、密实砂土层贯入过程中受到的贯入阻力随深度变化规律。从图3（a）可以看出，SPH 值与CEL 值呈现较为一致的规律，在正则化深度d/D 达到0.3 时，贯入阻力达到峰值550 kPa，两者间无明显差异；随着贯入深度继续增加，CEL 预测值稍小于SPH 值。这是因为桩靴贯入过程中底部将产生相当可观的超孔隙水压力并对贯入阻力产生较大影响，忽略孔压影响可导致最大误差接近10%；图3（b）为桩靴在密实砂土中贯入过程受到的阻力。桩靴阻力随正则化贯入深度逐渐增大至d/D=0.2，而后逐渐减小并稳定在550～600 kPa。两种方法预测的贯入阻力峰值约为680～700 kPa，均在d/D=0.2 时出现。然而，初始贯入阶段CEL 的结果呈现较为剧烈的振荡，原因是未能考虑密实砂土发生剪胀时孔隙率变化的影响。本文采用的算法对孔隙率建立单独的控制方程并求解，故可以考虑到这一点。

图3 桩靴贯入阻力随正则化贯入深度变化Fig.3 Penetration resistance versus normalized penetration depth

2.2 黏土中贯入模拟及孔隙水压力分析

由于黏土渗透系数较小，桩靴贯入过程中周围土体内部会产生较大的超孔隙水压力，而后随着时间逐渐消散，对桩靴工作阶段的安全性有很大影响。早期Hossain 等[4]、Teh 等[9]采用LDFE 对桩靴连续贯入过程进行了模拟，但由于采用的是总应力分析方法，无法有效计算孔隙水压力。Purwana 等[16]采用离心机试验方法对桩靴在正常固结饱和黏土中的连续贯入过程进行了模拟。图4 中，T1～T4 为总应力测点，P1～P8 为孔隙水压力测点。试验在100g加速度环境下进行，根据相似准则等效于直径12.5 m的桩靴连续贯入土中深度达19 m。SPH 模型与Purwana 等[16]的离心机模型试验对应的原型尺寸保持一致且材料参数完全一致，水的相关参数为μ=0.001 Pa·s,000 kg/m3, cf=142.0 m/s，黏土相关参数 为600 kg/m3, kE=520 kPa/m, E=6.5 MPa,n=0.63, k=2.0×10−7m/s, υ=0.33, c=1 kPa, ϕ=23°, ψ=0°，几何尺寸为HW=5.0 m, HSW=30.0 m, WSW=36.0 m,D=12.5 m, Lb=2.0 m, Lm=1.0 m, Lt=1.5 m，其中，kE为杨氏模量沿深度方向变化梯度，其他参数意义同上。为了减少计算量，仅模拟桩靴的前10 m 贯入过程。

图4 桩靴贯入离心机模型（单位：mm）Fig.4 Centrifuge model set-up for spudcan penetration (unit:mm)

图5 和6 分别为桩靴贯入不同深度时土体内产生的孔隙水压力及超孔隙水压力云图。可以看出，d/D=0 时，土体内部孔隙水压力呈现出静水压力分布规律，超孔隙水压力为零。d/D=0.4 时，桩靴周围产生最大值约为60 kPa 的超孔隙水压力，并且沿深度方向逐渐衰减至18 m 处，沿水平方向逐渐衰减至13 m 处。地表产生约1.0 m 的隆起变形，并随着贯入过程继续形成柱状的孔洞直至达到某一临界深度之后发生回淤现象。d/D=0.8 时，回淤的土体完全覆盖桩靴底部，这与Purwana 等[16]室内离心机试验观测到的现象一致。桩靴周围产生超孔隙水压力最大约为130 kPa，随深度逐渐衰减至26.0 m 处。

图5 桩靴贯入过程中孔隙水压力分布云图（单位：kPa）Fig.5 Contours of pore water pressure during spudcan penetration (unit: kPa)

图6 桩靴贯入过程中超孔隙水压力分布云图（单位：kPa）Fig.6 Contours of excess pore water pressure during spudcan penetration (unit: kPa)

图7 为桩靴贯入过程中顶部（P1，P2）及底部（P3，P4）4 个测点的孔隙水压力，纵坐标为正则化贯入深度d/D，横坐标为正则化孔隙水压力，其中γw为水的重度，D 为桩靴的直径。为便于对比分析，图7 中给出了Purwana 等[16]的离心机试验测值及Yi 等[17]的不排水模拟结果。从图7（a）和（b）可以看出，d/D<0.4 时，由于土体尚未发生回淤，桩靴顶部无超孔隙水压力产生，SPH 与Yi 等的结果无明显差异且均与静水压力曲线重合。离心机测值稍大于理论值，可能是由于测量误差。d/D>0.4 时，土体逐渐回淤覆盖桩靴并受到其拖拽作用向下位移，产生较小的负超孔隙水压力，故图7（a）中SPH 结果及Yi 等的结果均稍小于静水压力。相比较之下，桩靴底部在贯入过程中孔隙水压力远大于静水压力且大致随深度d/D 线性增加，如图7（c）和（d）所示。d/D=0.8 时，离心机测值及SPH 计算得到的均为2.25，而Yi 等的结果约为2.7。原因是Yi 等采用了完全不排水的假定，故计算结果偏大。

图7 贯入过程中桩靴顶部及底部正则化孔压Fig.7 Normalized pore water pressure at top and bottom of spudcan during penetration

图8 为桩靴贯入过程中顶部（T1，T2）及底部（T3，T4）的总应力，纵坐标为正则化贯入深度d/D，横坐标为正则化竖向总应力σzz/(γD)，其中γ 为混合物的重度。总应力σzz根据回淤土体的厚度及混合物的重度计算。由于土体回淤时刻无显著差异，均在d/D=0.13～0.15 时发生，故总应力数值相差不大。桩靴顶部σzz/(γD)随贯入深度可近似看作线性变化，d/D=0.8 时约为0.6；桩靴底部σzz/(γD)在贯入过程初期即d/D<0.3 时呈非线性变化，而后随d/D 线性增大，d/D=0.8 时约为1.4～1.5 。桩靴顶部T1，T2 处，SPH、离心机测值及Yi 等的结果无显著差异，而桩靴底部T3，T4 处差异较大。d/D=0.8 时，SPH 与Purwana 等结果相差近0.25，原因可能是本文土体采用了Drucker-Prager 屈服准则，不能反映出土体的体积屈服现象。然而需要说明的是，本文的目的是验证土-水-结构耦合SPH 算法对大变形贯入问题的适用性，而非提出或改进土体的本构模型，为了简化起见采用了经典的理想弹塑性土体本构模型。相比较之下，Yi 等[17]的计算结果与离心机试验测值误差几乎达到30%，说明本文所采用的算法相较于CEL 对于大变形问题更加适用。

图8 贯入过程中桩靴顶部及底部正则化总应力Fig.8 Normalized total stress at top and bottom of spudcan during penetration

3 结 语

为了克服传统网格类数值方法遭遇的网格畸变问题，基于土-水-结构耦合SPH 无网格方法对纺锤形桩靴在饱和砂土及黏土中连续贯入过程进行模拟，研究了贯入阻力、孔隙水压力、超孔隙水压力及总应力在土体发生极大变形情况下的变化规律。主要结论如下：

（1）该算法能有效捕捉大变形情况下的土-水混合物自由面特征及贯入阻力，不会发生网格畸变等问题，并且能够将土体、水及结构物三者之间的耦合作用影响计入其中。

（2）桩靴顶部孔隙水压力在贯入过程中近似静水压力分布，桩靴底部正则化孔隙水压力近似线性分布，d/D=0.8 时，约为2.25；桩靴顶部土体中竖向总应力在贯入过程中线性增加，d/D=0.8 时，底部正则化竖向总应力σzz/(γD)约为1.4～1.5。相同条件下，不考虑土-水耦合作用的CEL 近似解误差接近30%。

（3）SPH 无网格法可以作为求解岩土工程大变形问题的有力工具。