高聚物防渗墙在交通荷载作用下的应变特征

2020-09-07郭成超杨建超石明生蔡兵华李忠超

水利水运工程学报 2020年4期

郭成超，杨建超，石明生，关欢，蔡兵华，李忠超

(1.中山大学土木工程学院, 广东广州 510275；2.郑州大学水利科学与工程学院，河南郑州 450001；3.武陟裕泰房地产开发有限公司，河南武陟 454950；4.西南交通大学土木工程学院，四川成都 610031；5.武汉市市政建设集团有限公司，湖北武汉 430023)

堤坝是水利枢纽工程中最重要的建筑物，也是涉及水利工程安全的关键所在，其中防渗墙是堤坝防渗的重要组成，防渗墙的安全直接关系到整个枢纽工程的安全。传统的防渗墙技术主要有水泥搅拌桩地下成墙技术[1]、高压旋喷桩成墙技术[2]、混凝土连续墙技术[3], 这些传统的防渗技术存在设备庞大笨重、施工场地要求高、对堤坝扰动破坏较大、对周边水质土壤及环境可能造成污染、施工期较长、造价高、耐久性差等缺点。高聚物防渗墙作为土质堤坝防渗加固的新型防渗技术，具有施工快捷方便、防渗性能优良、材料绿色环保、耐腐蚀、性价比高、抗震抗裂性能好等优点，在实际工程中得到了越来越广泛的应用[4-6]。高聚物防渗墙是否完整对于堤坝防渗性能有着不言而喻的影响。目前国内外对高聚物的研究主要在注浆材料特性、注浆工艺和施工效果以及疲劳破坏、静动力响应特性等方面[7-11]，尤其是郑州大学联合多家单位攻关，研发了高聚物注浆快速维修成套技术，取得了良好的施工效果。在数值模拟方面，徐建国等[12]对比分析了高聚物防渗墙与混凝土防渗墙在静力与地震荷载下的应力分布及破坏特性的差异，发现同种工况下高聚物防渗墙应力最小，不易发生破坏；徐建国等[13]还在考虑实际工程条件基础上，建立坝体正常蓄水情况下高聚物防渗墙堤坝应力场与渗流场耦合分析的数值模型，结果表明不考虑渗流与应力耦合作用时坝体和墙体的位移和应力计算结果偏小；李嘉等[14]利用有限元软件ABAQUS 建模分析，考虑堤坝墙体、坝体材料接触弹塑性单元，得到了墙体的地震反应规律。

但是，目前国内外对于高聚物防渗墙成墙后受交通荷载作用下的沉降及应力应变特征分析鲜有涉及。鉴于此，本文依托武汉江北快速路城市滨江道路堤坝工程，对高聚物防渗墙在静载、偏载及冲击荷载作用下的应变特征进行研究，并与现场模型试验进行对比，分析土体沉降、高聚物防渗墙墙体变形规律等，为进一步改善高聚物防渗墙设计及施工提供参考和指导，对高聚物防渗墙的应用推广具有一定的意义。

1 高聚物防渗墙计算模型

1.1 本构模型

本文研究堤坝高聚物防渗墙问题中土体采用的是Mohr-Coulomb 弹塑性模型。此模型涉及弹性模量E、泊松比μ、土体内摩擦角φ 和黏聚力c，参数物理意义明确，能反映实际工程情况。

模型采用的屈服函数[15]为：

式中： Θ为极偏角。

1.2 接触面分析

本文采用无厚度的古德曼单元模拟防渗墙体与周围土体的相互作用[3,7]。古德曼模型的本构关系是用双曲线方程来描述的，通过接触单元的法向和切向2 个关系式来反映。如设Fs和Fn分别为接触单元间的摩擦力和法向力，则有：

式中：Fsi为初始摩擦力；Kn为法向刚度；Kt为黏性系数；d 为接触点距离；u 为切向位移。

1.3 模型材料

本文研究包含3 种材料，其一是下部长、宽、深分别为20，15 和3 m 的路基土；其二是高5 m、坡比为1∶1 的路堤土；其三是高、厚、长分别为8，0.04 和10 m 及密度为0.24 g/cm3的高聚物材料。详细的材料参数如表1 所示。

考虑到防渗墙在试验及工作状态下，最大压应力达不到1 MPa，因此在进行ABAQUS 数值模拟时，高聚物材料采用线弹性模型。

表1 材料参数Tab.1 Material parameter table

1.4 荷载及边界条件

根据模拟调试结果，防渗墙荷载影响深度为6 m，影响宽度为4 m，考虑尺寸效应，兼顾模型计算量，建立如图1 所示的三维实体模型，为了与现场模型试验进行对比分析，将防渗墙设置于堤坝正中间。

模型中荷载类型为大车静载、大车偏载、落锤冲击荷载。冲击荷载形式为 P=Asin(πt/0.03)，A 表示5 t，4 t，3 t 对应的荷载峰值，时间周期为0.03 s，现场试验中冲击荷载取实测动态数据，时间周期为0.06 s，将5 t 落锤冲击荷载作为标准荷载作用输入，3 t 和4 t 的分别乘以相应的系数。

图1 模型网格划分Fig.1 Model meshing

创建边界条件FIX-X、FIX-Y 和FIX-Z，表示约束模型的前后、左右下部及坝坡面的位移。考虑到实际工程经过了半年的固结沉降，应先进行初始应力平衡，将计算初始应力场导入坝体模型，得到模型的初始应力状态，其初始位移变为0。

网格划分采用Standard 单元库，线性几何阶次、减缩积分以及沙漏控制，局部进行网格加密处理。网格划分如图1 所示。

2 静力荷载结果与分析

2.1 静力荷载计算结果分析

静力荷载模拟分为以下两种作用荷载：（1）大车正载。大车后轮实际轴距2 m，在防渗墙两侧1 m 位置处，通过在两个20 cm×30 cm 的矩形范围内施加均布荷载实现大车静载的施加；（2）大车偏载。荷载位置较正载偏移0.6 m，荷载大小不变。最终得到高聚物防渗墙横向应变εx和竖向应变εy云图（图2）。

图2 大车正载和偏载作用下的横向应变和竖向应变云图Fig.2 Contours of lateral and vertical strains under normal and offset loads

通过对0～8 m 深度范围内高聚物防渗墙在正载和偏载作用下的横向应变εx和竖向应变εy随深度变化规律（图3）的对比分析发现，荷载位置的变化并不影响应变曲线的整体变化趋势。就应变大小而言，横向应变εx和竖向应变εy随深度均呈现先快速增大至峰值后逐渐减小最后趋于稳定的规律，但偏载作用下的应变均大于正载作用下的应变。偏载横向应变εx与正载横向应变εx曲线几乎重合，说明相同荷载情况下，坝面Z 方向荷载位置对横向应变影响不大。在1.5 m 深度范围内，偏载竖向应变εy大于正载竖向应变εy，其峰值应变是正载作用下的1.3 倍，深度超过1.5 m 后，应变曲线几乎重合，这说明荷载位置的改变仅对1.5 m 深度范围内的竖向应变产生影响。

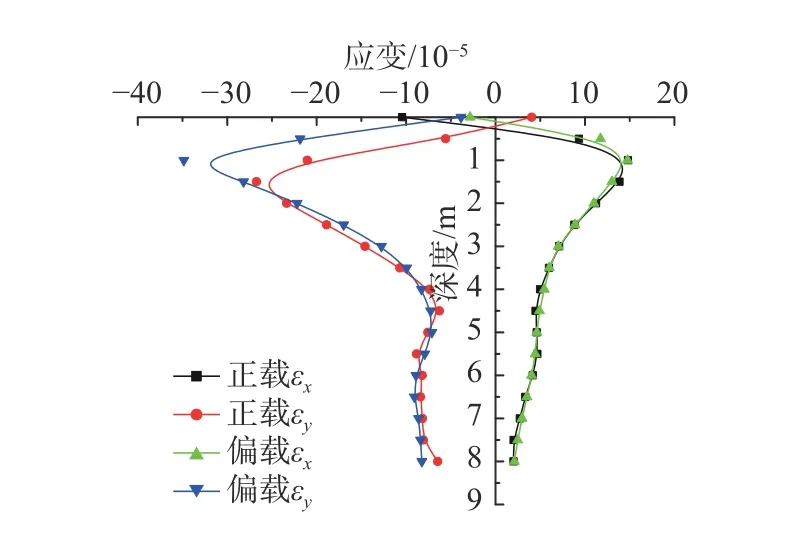
图3 静载作用下应变随深度的变化Fig.3 Strain variation with depth under static load

2.2 静力荷载试验值与模拟值对比

受试验条件所限，静力试验实测深度为2.1 m，因此，模拟深度取至2.5 m，则静力荷载作用下应变ε（横向应变εx和竖向应变εy）随深度变化的模拟值和试验值对比如图4 所示。由图4 可见：

（1）高聚物防渗墙在静力荷载作用下应变随深度呈现先增大后减小的变化规律。1.2 m 深度范围内应变随深度增加而增大，在1.0～1.2 m 深度达到应变峰值，且偏载作用下的应变峰值大于正载作用下的应变，从力学机制上分析，正载和偏载的数值相同，偏载作用在防渗墙上的等效力是正载与偏弯矩之和，因此偏载对防渗墙应变影响较大。当超出1.2 m 深度范围，防渗墙应变随深度增加而减小，这说明静力荷载对防渗墙应变的影响范围基本为1.2 m。

（2）正载作用下，高聚物防渗墙应变峰值对应的深度存在较大差异：横向应变在1.2 m 处达到试验峰值，在1.0 m 处达到模拟峰值，而纵向应变在1.5 m 处达到试验峰值和模拟峰值，这是因为防渗墙的网格划分为0.5 m，且采用线性插值绘制曲线，而现场试验中应变片间隔为0.3 m，故应变在1.0，1.2 和1.5 m 处达到峰值。

（3）正载作用下，土体应变模拟曲线与高聚物防渗墙应变试验曲线变化趋势相同，数值接近，体现了高聚物防渗墙的柔性特征，即与土体协调变形的能力，有利于高聚物防渗墙防渗功能和荷载作用下墙体路基整体性的发挥。

（4）偏载作用下，高聚物防渗墙应变试验值与模拟值存在较大差异：横向应变εx在0.9 m 深度范围内，模拟值大于试验值，0.9～2.1 m 深度处，试验值较大，且在1.2 m 处达到峰值，较模拟结果上升0.2 m。竖向应变εy仅在0.7～1.3 m 深度范围内试验值大于模拟值，且在0.9 m 深度达到峰值，较模拟结果上升不足0.1 m，考虑到应变片粘贴距离，此误差可忽略不计。

图4 静载作用下应变随深度变化的模拟值和试验值对比Fig.4 Simulated and experimental strains versus depth under static load

3 冲击荷载结果与分析

本文主要针对防渗墙在相同位置受到不同荷载及在不同位置受到相同荷载作用时的两种情况进行分析，由于受现场试验条件的限制，冲击荷载通过落锤式弯沉仪施加，而验收的荷载通常只是5 t，鉴于施加在堤坝顶面，因此施加的荷载不超过5 t，本文施加的落锤动态荷载为3，4 和5 t。具体位置见图5，位置1 位于防渗墙正上方，位置2 距离防渗墙0.8 m 荷载处，位置3 距离墙体1.6 m。

图5 冲击荷载位置Fig.5 Location of impact load

3.1 冲击荷载结果分析

3.1.1 相同位置作用不同荷载位置1～3 施加不同的落锤动态荷载后，防渗墙的横向应变与竖向应变变化规律如图6 所示。可见，在堤坝同一位置施加不同荷载作用时，防渗墙的横向应变和竖向应变（不考虑正负号，正负代表拉压）均呈现先快速增大至峰值后减小至稳定状态的三段式变化规律。

图6 位置1～3 施加不同荷载的竖向应变Fig.6 Lateral and vertical strains when applying different loads at positions 1～3

（1）快速增大阶段：在该阶段防渗墙横向应变和纵向应变均快速增大至峰值，应变曲线的增大速率随荷载的增加而增大。就应变峰值对应的深度而言，荷载作用在位置1～3 时防渗墙分别在0.5，1.0 和2.1 m 深度处达到横向应变峰值，在0.6，1.5 和2.1 m 深度处达到竖向应变峰值。这说明，荷载对高聚物防渗墙竖向应变的影响较大；同时也说明，在荷载作用位置不变的条件下，荷载大小不会影响应变峰值对应的深度。就应变峰值的大小而言，竖向应变峰值较横向应变峰值大，尤其是位置1 处，竖向应变峰值比横向应变峰值高出1 个量级，这进一步说明冲击荷载主要影响防渗墙的竖向应变。

（2）应变减小阶段：在该阶段防渗墙横向应变和纵向应变均逐渐减小，其范围大致为4～5 m，即在应变达到峰值后的4～5 m 范围内防渗墙应变逐渐减小，尤其是在初始的1 m 范围内，应变快速减小，基本符合应变曲线的减小速率随荷载的增加而增大的规律。

（3）趋于稳定阶段：在该阶段防渗墙横向应变和纵向应变均趋于稳定，应变降为峰值的10%～20%左右，在6 m 深度处出现3 条应变曲线重合的趋势，说明防渗墙的影响范围为6 m，即防渗墙在6 m 范围内能够起到抵抗变形的作用。

3.1.2 不同位置作用相同荷载选取典型标准冲击荷载5 t 作用下的横向和竖向应变进行分析（图7），其他吨位荷载规律类似。

（1）不同位置处作用相同荷载时应变曲线在防渗墙4 m 深度范围内差异较大，但4 m 后应变曲线逐渐重合，具体表现为位置1 处的应变减小速率最大，位置2 次之，位置3 最小，且应变峰值也符合上述顺序，应变减小幅度越大表明防渗墙的吸能效果越好，而由于荷载作用位置在防渗墙横向上的差异，吸能效果明显不同，表现为荷载作用位置与防渗墙之间横向距离逐渐增大，防渗墙的吸能效果逐渐减弱。

（2）竖向应变与横向应变峰值并不出现在同一深度，竖向应变的峰值深度大于横向应变的峰值深度，说明荷载作用位置主要影响防渗墙的竖向应变；防渗墙竖向应变大于横向应变，且越接近防渗墙相差越明显，说明防渗墙在受到外界荷载作用时，竖向应变响应强于横向应变响应，即防渗墙竖向吸能效果强于横向。

图7 5 t 荷载作用下不同位置的横向和竖向应变Fig.7 Lateral and vertical strains when applying 5 t load at different positions

3.2 防渗墙变形分析

因数据种类过多，且由3.1 节模拟结果可知，荷载对竖向应变的影响大于横向应变，故重点分析不同位置的冲击荷载对高聚物防渗墙竖向变形的影响。

取落锤荷载4 t 作为典型荷载值，分别作用在位置1，2 和3，从模拟结果中提取0.5，1.0，1.5 和2.0 m 深度位置应变时程曲线；现场试验应变片的粘贴间距为0.3 m，选取的点深度分别为0.6，0.9，1.5 和2.1 m，分别代替0.5，1.0，1.5 和2.0 m，不考虑0.1 m 深度差值的影响，但由于试验条件的限制，只能在需要测定的深度位置布置应变片，得到的结果是施加冲击荷载后达到荷载峰值时对应的峰值应变，曲线形式与模拟曲线存在较大误差，但模拟应变时程曲线中的峰值应变与试验中的峰值应变是对应的，因此本文只针对以上两种峰值应变进行对比分析。同时由于防渗墙竖向受压，现场实测值为负，因此，为了便于观察和对比分析，模拟值和试验值均取绝对值进行分析，如图8 所示。图8 中4 t-1，4 t-2，4 t-3 表示4 t 荷载分别作用在位置1，2，3 时的应变值。

图8 竖向应变时程曲线Fig.8 Vertical strain time history curves

对比分析图8 可知：

（1）冲击荷载作用在位置1、2 时，防渗墙不同深度处竖向应变由大到小依次为：0.5 m 处，1.0 m 处，1.5 m处和 2.0 m 处；但在位置3 时，竖向应变由大到小依次为1.5 m 处，1.0 m 处，0.5 m 处和2.0 m 处。应变峰值的试验值与模拟值相对误差较小，最大相对误差为20%左右（图8(c)和(d)），最小相对误差为1%左右（图8(a)和(b)），表明试验值与模拟值基本吻合。

（2）从图中可以直观地发现，当冲击荷载作用在同一位置时，随着深度的增加，应变峰值也基本减小，说明随着深度的增加，落锤传递的荷载产生了衰减，进一步表明高聚物防渗墙可以吸收一部分的冲击能量，表现出一定的柔性特征。

（3）荷载作用位置与防渗墙之间距离增加，同一深度处高聚物防渗墙的应变峰值减小，以2.0 m 深度的应变为例，该深度对应的应变从7.02×10-4降低至3.26×10-4，这说明荷载作用位置对防渗墙的竖向应变影响较大。