基于Weibull分布和SVR的城轨列车自动进站停车精度预测方法

王 峰，黄友能，何占元，徐田华， 唐 涛

(1.北京交通大学 电子信息学院，北京 100044；2. 朔黄铁路发展有限责任公司，河北 沧州 062350；3. 北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044)

为满足城市轨道交通运营效率不断提升的需求，越来越多的城市轨道交通采用列车自动运行的方式。列车自动运行不仅能够提高运输效率、降低司机劳动强度，还可以减少由于人工误操作对运营带来的影响。列车自动进站停车是列车自动运行中的一个重要功能，而停车精度是列车在不影响运营安全的气象条件下运行时，衡量列车自动进站过程中，是否满足执行列车车门和屏蔽门正常联动功能的最重要的触发条件。

目前，学者对城轨列车自动停车精度(Train Parking Error, TPE)的研究可总结为以下两个方面：一是列车自动进站停车算法，主要采用的控制算法有经典控制算法、参数自适应控制算法、智能控制算法、集成智能控制算法[1-3]，这些算法研究通常是从保证站间运行时间、列车节能等角度开展，但当一条线路投入运营后，就不再调整算法。二是列车制动闸瓦特性，城轨列车进站停车过程中所需的制动力，主要由电制动提供，仅在速度低于3 km/h时才施加空气制动使列车停稳。文献[4-6]分析总结了国内外闸瓦磨损规律和使用寿命，列车闸瓦的理论使用年限较长，可达7～9年。

可以看出，在城轨线路投入运营后，列车自动进站停车算法通常不再调整。同时，从列车闸瓦理论使用年限来看，较长时期内不会更换闸瓦，但随着列车运行里程的增加，闸瓦的磨耗会导致列车制动性能变化，影响到列车进站停车算法中所依赖的参数，从而导致进站停不准的情况发生。目前，针对此类问题，维护人员每日对车载设备记录的自动进站停车数据进行分析，根据停车精度的偏移程度决定是否进行维修调整，显然这种方式效率较低、劳动强度大。如果能够预测列车自动进站停车精度的偏移情况，可指导维护人员依据其变化趋势及时调整进站停车算法中的参数配置，从而可以大大减少列车上线运营后由于停不准引起的车门屏蔽门无法联动的问题，对运营水平和维护效率的提高具有重要意义。

因此，本文提出一种停车精度预测方法，首先通过Weibull分布拟合各期停车精度的分布，进而采用支持向量回归(Support Vector Regression, SVR)模型对停车精度分布进行预测，最后以北京地铁某条线一列车的停车精度数据对提出的模型进行仿真验证。

1 停车精度预测模型框架

图1为停车精度预测的主要流程，主要包括以下几个步骤：

Step1停车精度数据预处理。首先，给定历史进站停车精度数据库后，依据现场维修需求，以单位时间均匀分割历史数据为T期，每一期将作为一个分布样本。

Step2拟合各期数据的分布。Weibull能够表达多种分布，例如指数分布和正态分布等，具有很强的适应性[7]，在工程领域有着广泛的应用。因此，采用Weibull分布对每一期数据进行拟合，每一期将得到两个分布参数的估计值，即尺度参数和形状参数。对各期数据进行拟合后，得到两个分布参数的时间序列，即有待构建预测模型的两个时间序列。

Step3预测模型的构建与预测。在两个时间序列基础上，采用支持向量回归算法分别构建两个时间序列预测模型，通过构造的模型对下一期的分布情况进行预测。

Step4分布的分析与应用。通过分析下一期分布的参数和数字特征，如期望和方差等，可对下一期停车精度的情况作出评估，从而确定维修的必要性。

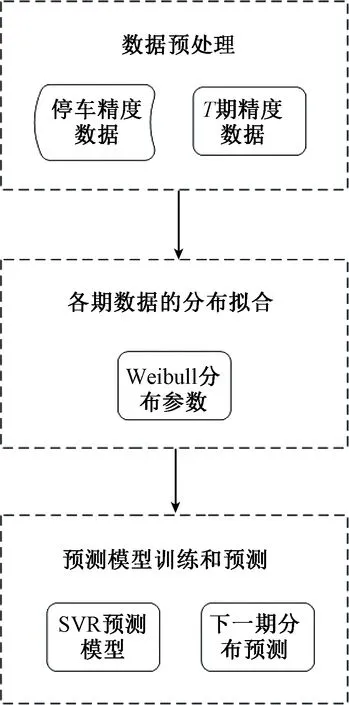
图1 停车精度预测算法框架

2 停车精度分布构造

Weibull 分布函数具有较好的适用性，在工程领域有着广泛应用[8]。因此，本文采用Weibull分布对停车精度数据进行分布拟合。数据分期后，对各期停车精度分布数据进行Weibull分布拟合，得到分布参数。

2.1 Weibull分布

假设随机变量X服从Weibull分布(随机变量的观察值是每期数据)，则X的概率密度函数为

( 1 )

分布函数为

( 2 )

式中：α>0 为尺度参数；β>0为形状指数。其中，Weibull分布中两个参数都与停车精度分布特征因子有关。α>0代表停车精度的分布的离散程度；β>0决定停车精度的偏度，是分析停车精度分布动态的依据之一。

2.2 Weibull分布的参数估计

Weibull分布参数估计方法主要包括：最大似然估计法、矩估计法、线性回归估计[9-10]。由于最大似然估计是一种简单有效的参数估计方法，本文采用最大似然法对Weibull分布的参数估计。

根据最大似然估计法，Weibull分布的最大似然函数可以表示为

L(x1,x2,…,xn;α,β)=

( 3 )

对上式两边取对数可得

lnL(x1,x2,…,xn;α,β)=

( 4 )

为求解上式的极大值，令∂lnL/∂α=0 和∂lnL/∂β=0，求解得到。即对以下二元一次方程组求解：

( 5 )

上述方程组可由数值解法求得参数α和β。

3 基于支持向量回归的预测算法

支持向量回归在很多领域已有广泛的应用，取得了良好的效果。为了对下一期停车精度分布进行预测，以参数时间序列为基础，采用支持向量回归构建其预测模型。

3.1 支持向量回归原理

文献[11]提出一种基于结构风险最小化的统计学习算法，称为支持向量机(Support Vector Machine, SVM)。目前SVM已在很多领域得到了广泛应用，除模式识别领域之外，有学者通过改变SVM的损失函数，将其构造为一种可用于回归分析的算法，称为支持向量回归[12-13]。

支持向量回归的核心思想可表述为：给定数据样本集(x1,y1),…,(xm,ym)。为实现线性可分，通过构造一个非线性映射φ(·)将样本特征空间x映射到高维特征空间F。新特征空间F线性回归表示如下

f(x)=w·φ(x)+bφ:Rn→Fw∈F

( 6 )

式中：b为偏置；w为回归系数向量。与传统的统计学习不同，SVR通过结构风险最小化，来寻找一个合适的函数f。它能够有效克服过拟合问题，有良好的泛化能力。由于引入了ε-敏感损失函数，结构风险最小化可以表述如下

( 7 )

式中：C为惩罚因子；m为样本数目；Θε(f(xi),yi)为ε-敏感损失函数，数学描述如下

( 8 )

线性不可分时，上述优化问题将得不到最优解。因此，引入松弛因子ξ和ξ*，来保证解的存在性。SVR的原问题可看作一个二次规划问题，形式如下

s.t. (w·φ(xi)+b)-yi≤ε+ξi

( 9 )

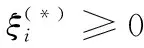
依据拉格朗日乘子法和对偶理论，可求得上述优化问题的对偶问题，表述如下

(10)

式中：K(xi,xj)为核函数，对偶问题的结果依赖于核函数K(xi,xj)(i=1,2,…,l)和常数C。

核函数的不同决定了不同形式的SVR回归模型。其中，常用的核函数有Sigmoid核函数、径向基核函数(RBF)、线性核函数等。本文采用RBF构建SVR模型为

K(x,xi)=exp(-γ‖x-xi‖2)

(11)

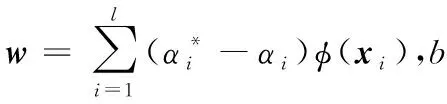
(12)

3.2 预测模型

算法1给出了预测模型构造及预测的详细步骤，以下进行阐述：

首先，以时间间隔τ(根据现场维修需求调研得到)对停车精度数据集D进行划分，得到T期原始数据分组。然后，分别对T期数据的每一期进行处理：构造精度数据Dt的原始分布Xt；归一化原始分布Xt后，得到分布Yt；对Yt进行Weibull分布拟合，估计出t期分布的参数αt,βt，即尺度和形状参数。重复以上步骤，得到了各期Weibull分布的参数时间序列αt,βt,t=1,2,…,T。

在此基础上，分割参数时间序列为训练序列αtrain,βtrain和测试序列αtest,βtest，并对SVR模型进行训练得到预测模型Mα,Mβ。在预测阶段，基于前几期的参数序列，对下一期的分布参数进行预测，得到下一期的分布参数αp,βp；最后，可构造出下一时期的停车精度分布，在反归一化后计算得到下一时期精度分布的分布特征，期望和方差；以此对列车的停车状况进行分析。

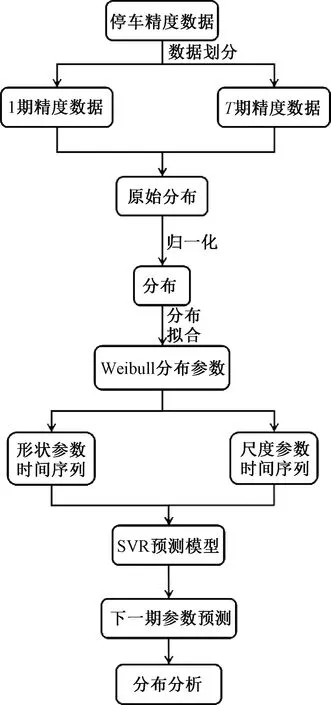
图2 停车精度预测算法步骤

算法1: 基于Weibull分布和SVR的停车精度预测

输入变量：停车精度数据D，数据划分时间间隔τ。

中间变量：各期精度数据Dt；原始分布Xt；归一化后的分布Yt；参数时间序列αt,βt,t=1,2,…,T；训练序列αtrain,βtrain和测试序列αtest,βtest。

输出结果：参数时间序列的预测模型Mα,Mβ。

(1)Dt←各期精度数据：按照时间间隔τ对停车精度数据D进行划分。

(2)fort=1,2,…,Tdo

(3)Xt← 原始分布：通过经验分布函数构造方法对各期精度数据Dt进行分布构造。

(4)Yt← 归一化分布：对原始分布Xt进行归一化操作，将分布值映射到[0,1]之间。

(5)αt,βt← Weibull分布参数：通过对Yt进行Weibull分布拟合，估计出各期分布的分布参数。

(6)end for

(7)αt,βt← 参数时间序列：由两个参数按各期时间顺序排列构成。

(8)αtrain,βtrain和αtest,βtest←训练序列和测试序列：由两个参数时间序列分割成得到。

(9)Mα,Mβ← 预测模型：由训练序列αtrain,βtrain作为SVR模型输入，通过训练得到。

(10)αp,βp← 预测结果：通过将待测时间序列分别输入对应预测模型预测得到。

(11)Ynext← 通过预测得到的分布参数构造出下一时期的分布。

(12)最后，对预测得到的分布进行反归一化并分析，如分布的期望和方差分析，进而给出列车停车状况的评估。

3.3 预测模型性能评价指标

3.3.1 统计指标

常用的预测模型的评价指标有：平均相对误差ARE和均方根误差RMSE等[14]。因此，本文采用这两种指标对预测模型效果进行评价

(13)

(14)

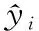
3.3.2 分布相似性度量指标

为度量预测分布和真实分布的相似性，引入分布距离指标，然后基于分布距离构造相似性指标。这里采用常用的Hellinger距离(以下简称H-距离)。H-距离是一种度量分布差异性的距离指标[15-16]。它的定义可表述为，给定两个离散概率分布P=[p1p2…pn]和Q=[q1q2…qn]，这两个分布的H-距离为

(15)

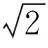
为了将分布差异性转化为分布相似性，定义基于H-距离的分布相似性为

DS(P,Q)=1-H(P,Q)

(16)

若H(P,Q)越大，则分布P和Q的差异性越大。假设分布P和Q分别代表预测分布和真实分布，则DS(P,Q)值越大，表示预测分布越接近真实分布。

4 实验分析

本文采用北京地铁某条线一列车三年来的自动进站停车精度数据，以间隔大于一年的两期分布数据为例说明停车精度变化情况。由图3可以看出，t+10期后的停车精度分布有向左偏移的趋势；无论是停车精度分布的峰值(位置参数相关)还是分布跨度(尺度因子相关)，都有一定量的变化。

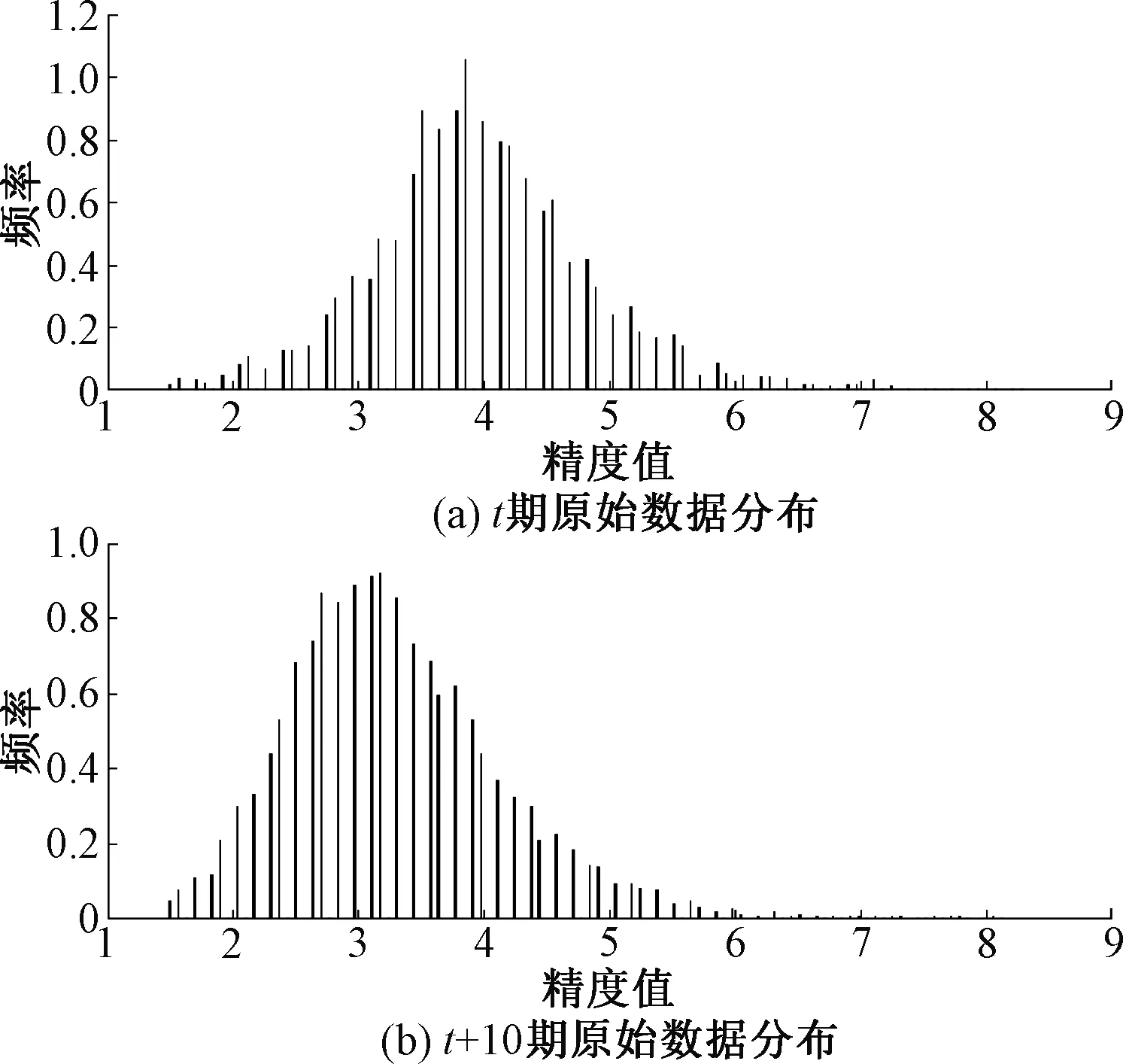
图3 停车精度经验分布的变化趋势

4.1 仿真分析

针对北京地铁某条线一列车自动停车精度统计值进行Weibull分布参数估计,得到的结果见表1(依据经验，时间间隔τ取30 d)。

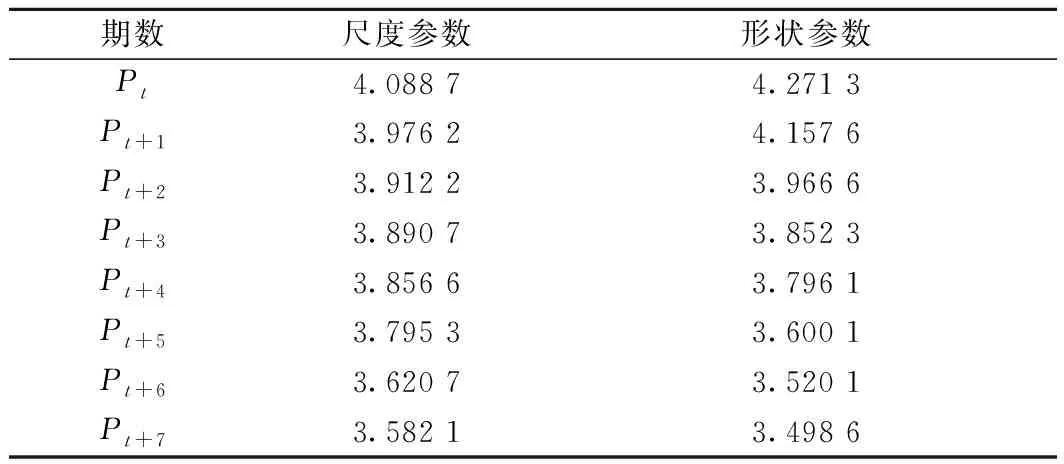
表1 停车精度Weibull分布参数

通过Weibull分布对8期停车精度数据进行拟合得到图4(横坐标和纵坐标分别为精度值和其概率密度值(pdf))。可以看出，从第t期到第t+7期的停车精度分布整体逐渐左移，且离散性变大。

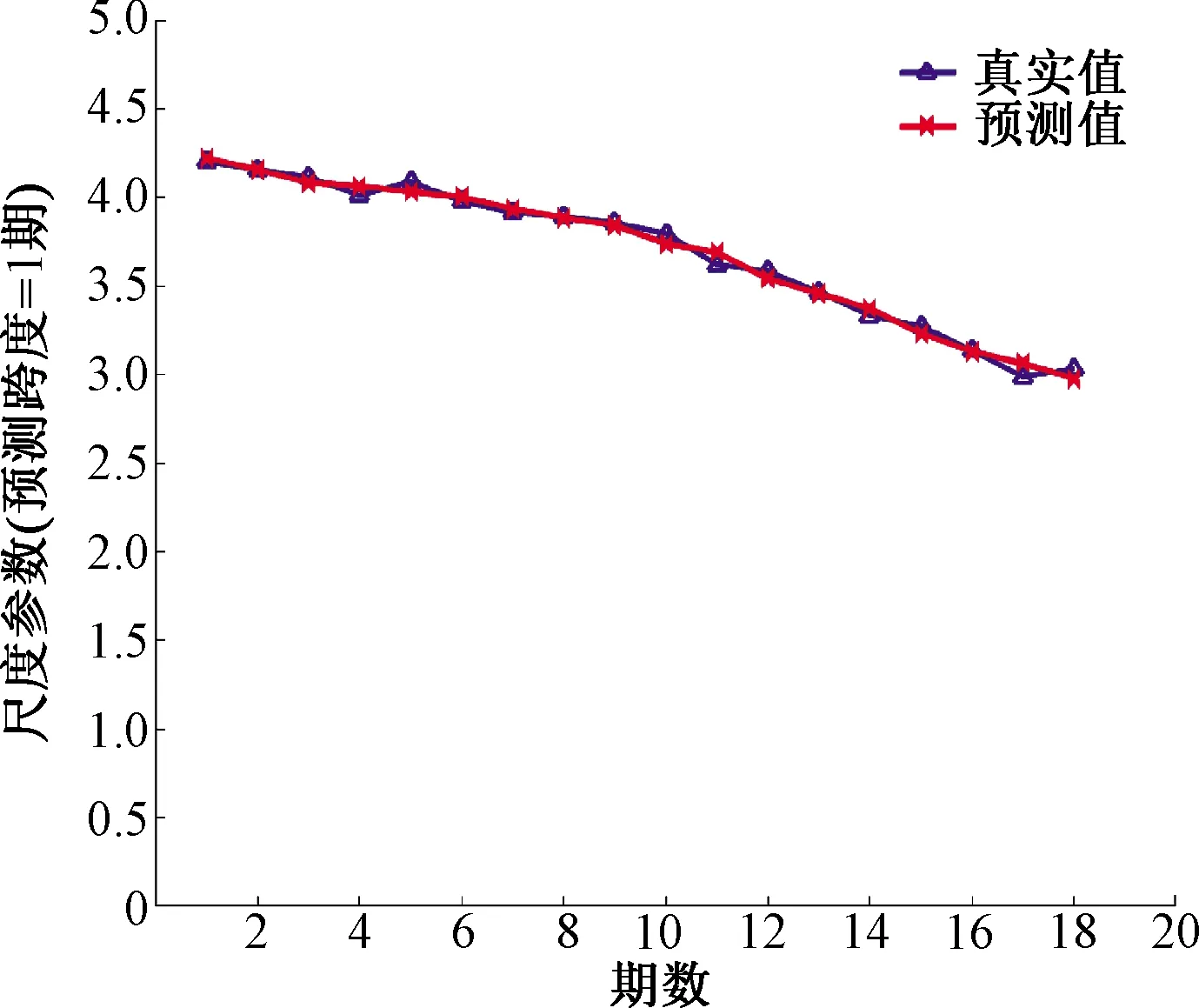
图5 尺度参数的实际值和预测值比较

4.2 预测结果

图5和图6分别是尺度参数时间序列α和形状参数时间序列β的预测结果。可以看出，提出的预测模型能够捕捉尺度参数和形状参数的变化趋势，准确地预测未来时期参数值。图7通过对比预测参数下的精度分布和真实分布，定性地展示了预测的效果。可以看出，停车精度分布的预测效果(归一化后)能够和原始各期分布基本吻合。

图6 形状参数的实际值和预测值比较

图7 停车精度预测分布和真实分布对比

表2从统计角度，通过RMSE和ARE指标评估了预测模型的表现效果，RMSE<0.09，两个参数时间序列的预测效果较好，从而验证了预测模型的有效性。

表2 预测结果的统计指标评价

图8从分布相似性的角度(反归一化后的预测结果与真实分布)给出了定量度量，预测分布和真实分布相似性的均值为0.953 3，验证了提出算法的有效性。

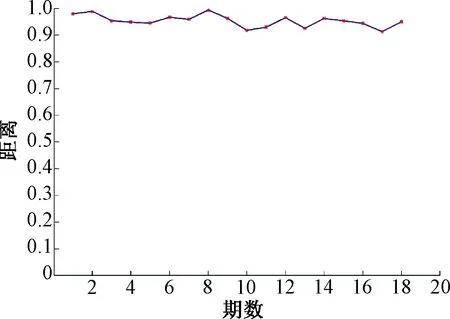
图8 预测分布和真实分布的相似性度量

5 结束语

本文通过对各期列车自动进站停车精度数据进行Weibull分布拟合，来描述各期列车自动停车的状态。进而，取各期Weibull分布的特征参数，即尺度参数和形状参数，来构造两个特征时间序列。在此基础上进行SVR模型训练，得到两个预测模型。采用预测模型对新一期的停车精度的两个特征参数进行估计，从而得到新一期的列车自动停车精度的分布情况。通过北京地铁某条线一列车自动进站停车精度数据的验证分析，说明了本文提出的停车精度预测方法的有效性和准确性。