动车组车轮多轴疲劳强度分析及修正

2020-09-07王悦东战庆文张金玉陈秉智

铁道学报 2020年8期

王悦东，战庆文，张金玉，陈秉智

(1.大连交通大学机车车辆工程学院，辽宁大连 116028; 2.中车长春轨道客车股份有限公司，吉林长春 130062)

车轮是铁道车辆走行部重要的组成部分，其强度与运行时的疲劳寿命一直是列车运行安全的重要评估参数，且车辆走行部的疲劳问题越来越显著[1]。车轮作为车辆运行重要的支撑部件，若该部件发生疲劳失效，其后果不堪设想。因此，在车辆尤其是高速动车组中，对车轮的设计参数及运行安全性能要求非常高。车轮的疲劳一般属于高周疲劳，其强度评估一直是研究的热点。

根据动车组车轮的结构及其运行特点，对于普通的轴对称车轮，应用单轴的疲劳准则就可达到强度评估的基本要求，应用的国际标准为UIC 510-5-2003标准[2]和BS EN 13979-1-2003标准[3]。评估非轴对称车轮疲劳时，单轴疲劳准则仍可以对具有对称性的辐板区域进行疲劳评估，但对于车轮辐板孔处等危险区域，单轴疲劳准则不再适用，应该使用多轴疲劳准则。多轴疲劳准则主要有Dang Van评估准则、Sines评估准则、Crossland评估准则以及Kakuno-Kawada评估准则等[4]。国内外很多学者都对列车车轮的疲劳强度评估做了相关的试验、理论研究以及开发应用。文献[5]对某非轴对称列车车轮进行疲劳评估，分别应用单轴疲劳强度方法、Goodman曲线评估法以及多轴疲劳强度Dang Van准则，给出了疲劳准则各自的安全度和应用范围。文献[6]基于有限元分析思想，采用Haigh疲劳评估图评估了S型、直型辐板车轮的疲劳强度。文献[7]应用Ansys软件进行疲劳算法二次开发，实现了多种车轮多轴疲劳强度评估程序化模块计算。综上所述，目前多数学者所提出的多轴疲劳研究方法均以对称扭转疲劳极限作为车辆车轮疲劳强度评估的标准，而在动车组实际运行过程中车轮的载荷工况及受力情况比较复杂，因此在评估准则中应该考虑扭转及弯曲等多种应力组合作用的影响。本文基于CRH3型动车组非轴对称车轮，选择Sines准则[8]、Crossland准则[9]和Kakuno-Kawada准则[10]，根据其算法编制相关程序，进行有限元仿真计算，对车轮辐板孔区域的多轴疲劳强度进行评估，计算各种多轴疲劳准则与方法的安全系数并进行对比分析；并且在Kakuno-Kawada 准则的基础上对其进行修正，同时考虑扭转应力和弯曲应力对动车组车轮疲劳的影响，提出更为可靠的动车组车轮疲劳强度评估方法。

1 非轴对称车轮疲劳评估

多数学者认为非轴对称车轮的疲劳评估要将其分成轴对称区域及非轴对称区域进行。一般车轮的辐板区属于轴对称区域，疲劳评估标准采用最大主应力准则[11-12]，按照单轴疲劳准则评估可靠性。车轮其他区域并不满足轴对称分布，如CRH3车轮的辐板孔及附近区域就是典型的不对称结构。因为3个受力方向都有可能很显著，不再是单轴疲劳问题，故选用多轴疲劳准则进行疲劳评估。

1.1 辐板非孔区域疲劳强度评估

在国际铁路联盟标准UIC 510-5-2003中，轴对称车轮疲劳评估采用单轴疲劳评估方法。其需要先将多轴应力状态转变为单轴应力状态，如图1所示，采用投影法计算得到所有工况下的平均应力σm和应力幅值σa。

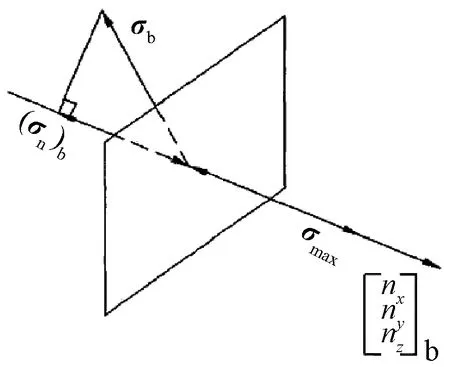
图1 多轴应力状态转变为单轴应力状态的方法

具体的计算为

( 1 )

式中：nx、ny、nz为方向余弦。

得到了某一方向的最大应力值和最小应力值，即可求出该节点所有工况下的平均应力值及应力幅值,即

( 2 )

( 3 )

采用Haigh-Goodman疲劳评估曲线对该车轮进行疲劳强度评估，并得到安全系数n。

( 4 )

1.2 辐板孔区域疲劳强度评估

针对辐板孔区域的受力特点，在对单轴疲劳进行评估的基础上，许多学者采用多轴疲劳方法进行计算与评估。其中Sines准则、Crossland准则以及Kakuno-Kawada准则是最常见的3种多轴应力评估准则。

Sines准则的计算公式为

( 5 )

( 6 )

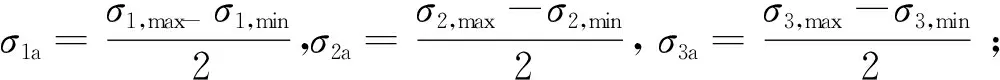
其中：

Crossland准则是另外一种常用的多轴疲劳准则，它不但考虑了静水应力的均值影响，还考虑了静水应力最大值对多轴疲劳强度的贡献，即

( 7 )

Kakuno-Kawada 准则由日本学者提出，在计算时将静水应力幅值引起的疲劳和均值引起的疲劳进行了区分,即

( 8 )

安全系数为

2 动车组车轮疲劳仿真分析

2.1 有限元离散模型

CRH3型动车组车轮为典型的非轴对称车轮[13]。应用Hypermesh软件建立车轮有限元模型，车轮整体选用三维六面体单元进行离散，网格划分如图2所示。在车轮的中心处增加了车轴部分模型，并在车轴两侧限制x、y和z三个方向的位移[14-15]。

图2 CRH3车轮有限元离散模型

2.2 疲劳载荷工况分析

根据国际铁路联盟标准规定，车轮在列车运行过程中可简化为3个疲劳载荷工况：

(1)列车直线运行时，车轮只受竖直力P1。

(2)列车过曲线时，竖直力P2与横向力H2同时作用。

(3)列车通过道岔时，竖直力P3与横向力H3同时作用。

( 9 )

式中：P0为车轮的轮重。每个工况在各计算截面上作用力的方向以及位置如图3所示。

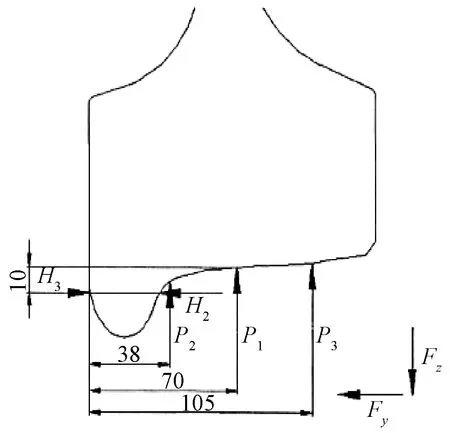
图3 各工况加载示意图(单位：mm)

2.3 评估位置选择

整个车轮可分成8块对称区域，每个区域如图4所示。分别选取辐板孔周围的两圈结点作为评估对象。

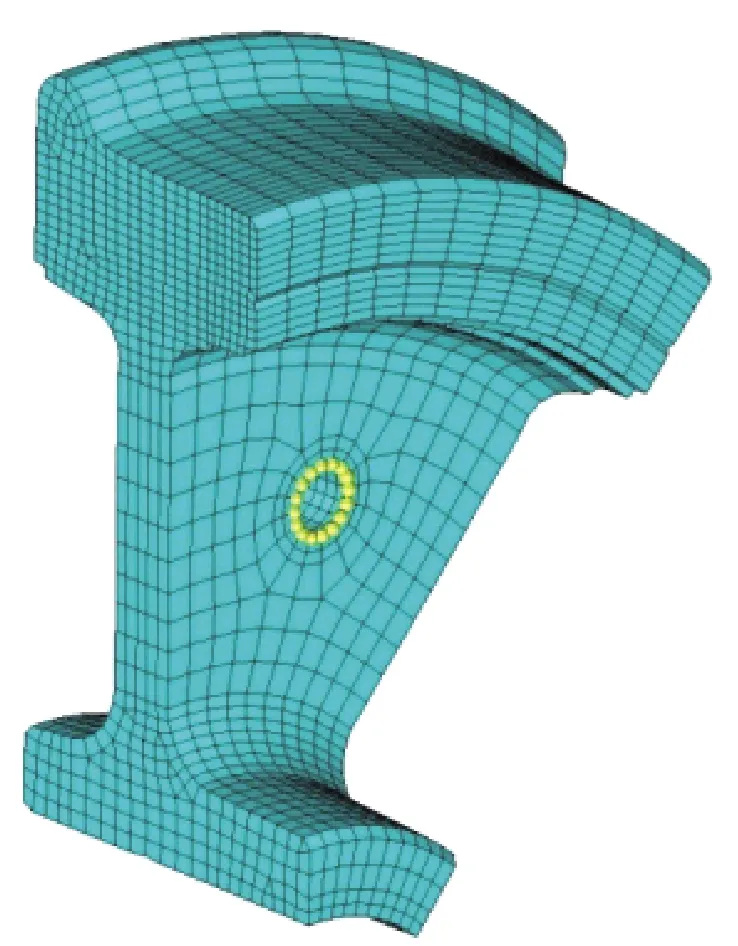
图4 车轮部分结构及评估点位置

3 疲劳计算结果对比

对于一般的钢材，对称弯曲疲劳的试验数据较易获得，但对称扭转疲劳极限数据较少，对称扭转疲劳极限t-1与对称弯曲疲劳极限f-1有一定比例关系，其比值介于0.48～0.75之间。 CRH3型动车组车轮的对称弯曲疲劳极限f-1为245 MPa[16]。对称扭转疲劳极限取其最大值，即t-1/f-1=0.75，从而可得t-1=183.75 MPa。

将Sines准则、Crossland准则和Kakuno- Kawada准则计算方法编制相应程序，通过Ansys软件计算得到疲劳评估结果。比较辐板孔评估点处安全系数大小，计算结果如图5所示。

图5 车轮辐板孔评估点安全系数

对图5数据进行比较，Sines准则、Crossland准则和Kakuno-Kawada准则最小安全系数分别为12.40、7.24、6.11。因此Kakuno-Kawada准则进行多轴疲劳评估时相对全面及安全，得到的结果也最保守。

4 修正Kakuno-Kawada准则

Kakuno-Kawada准则属于多轴疲劳强度评估方法，在早期的多轴疲劳研究中，通过对原试件进行弯扭疲劳试验后得出，依据循环加载下疲劳裂纹是否发生，将静水应力幅值和均值的影响分别考虑。

但鉴于动车组实际运行中载荷的复杂性，可能会同时对车轮产生弯曲与扭转应力并叠加在一起，对车轮疲劳状态产生较大影响，因此该疲劳评估准则有一定的局限性，需要修正其疲劳限定值。修正后的Kakuno-Kawada疲劳准则应能够考虑这两种情况同时对车轮作用时的影响，因此分别以t-1和f-1为修正目标。车轮辐板孔受力如图6所示。

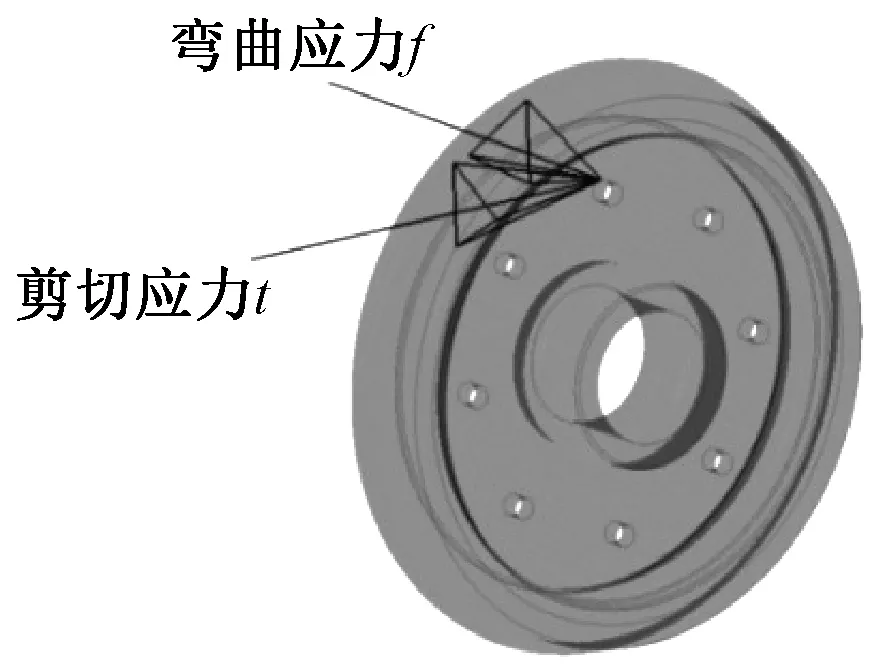
图6 车轮辐板孔的受力状态

修正后的准则将对称弯曲疲劳极限值f-1作为疲劳限定值，增加其限定条件。加入f-1后，式( 8 )可表示为

(10)

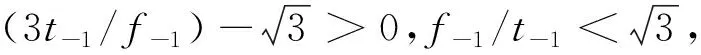
(11)

其中

根据Kakuno-Kawada准则可得

即

(12)

代入式(11)可得

(13)

由此获得修正后的Kakuno-Kawada准则为

(14)

将t-1和f-1合并，共同作为多轴疲劳评估的限定值，对式( 8 )等效变换，得到

(15)

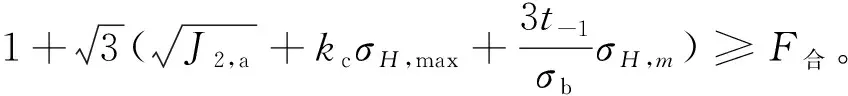
则式(14)与式(15)相加得到修正后的Kakuno-Kawada准则为

(16)

综合以上所得结果，整理后可得到修正后的Kakuno-Kawada准则为

(17)

将上述方法及相关数据提取进行程序化，并开发独立运行的程序进行车轮多轴疲劳强度评估，还需要将安全系数求解出来。

以f-1作为疲劳强度评估标准的修正准则，其安全系数为

以t-1和f-1同时作为疲劳强度评估标准的修正准则安全系数为

本文取对称扭转疲劳极限t-1和对称弯曲疲劳极限f-1的比值为0.75，故选择修正后以对称弯曲疲劳极限f-1作为评估标准的Kakuno-Kawada准则作为评估标准。通过计算得到修正后的Kakuno-Kawada准则安全系数和原Kakuno- Kawada准则安全系数，将结果数据进行绘制成折线图如图7所示。

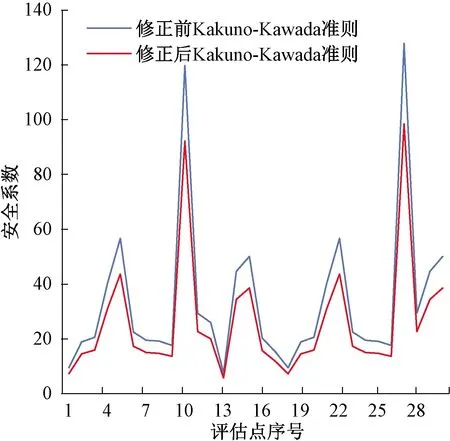
图7 修正前后的Kakuno-Kawada准则安全系数

将图7中修正前后的Kakuno-Kawada准则安全系数进行对比，发现修正后的Kakuno-Kawada准则安全系数小于修正前的Kakuno-Kawada准则安全系数。因为考虑到扭转应力和弯曲应力对车轮疲劳强度的影响，修正后的Kakuno-Kawada疲劳准则与动车组车轮实际运行受力情况更加相符，而且将t-1与f-1的比值作为多轴疲劳评估限定条件，考虑工况条件更加全面，也使得修正后的Kakuno-Kawada准则更加保守，安全性更可靠。在实际运用中，安全系数并不是唯一的考核标准，还需要考虑经济成本等因素。