基于Druck-Prager和MISO模型的混凝土三轴压缩行为有限元模拟

2020-09-07陈晓鹏西北有色勘测工程公司陕西西安710054

水泥工程 2020年2期

陈昊,陈俊,陈晓鹏（西北有色勘测工程公司，陕西西安 710054）

0 引言

经过一百余年发展，混凝土已然成为最重要的建筑材料之一，已广泛应用于工民建、路桥、水利和地下空间开发等工程领域[1,2]。实际工程中，混凝土结构内部多处于三向应力状态，不同的应力状态和应力历史常导致混凝土变形破坏特征呈现显著差异[3]。早在20世纪20年代，Richart等[4]就开展了混凝土圆柱试样的三轴受压试验。其后，随着岩石类材料三轴试验技术不断发展，高围压条件下混凝土常规三轴和真三轴试验得以开展，尤其在常规三轴试验方面获取了极其丰硕的数据，在一定程度上推动了混凝土本构模型的发展和完善[5]。目前，高性能常规三轴试验机凭借其日益完善的加载和量测技术已成为研究复杂应力状态和应力路径作用下混凝土综合响应行为的主要平台。如Imran等[5]在20世纪90年代中期采用液压伺服三轴试验机研究了不同应力水平条件下，混凝土含水率、孔隙度及应力路径对其变形破坏特征的影响。该试验共包含130组三轴试验，丰富了既有数据库的试验结果。本文采用AN⁃SYS软件对Imran[5]研究中饱和素混凝土（水灰比为0.4）部分常规三轴压缩试验进行有限元模拟，并分析对比Druck-Prager模型及MISO模型（采用Mises强度准则）的模拟结果。此外，在既有三轴压缩有限元模拟中，模型端部约束条件不尽相同，其主要反映了三轴压缩试验中试件端部摩擦力的影响[6,7]。因此，本文进一步基于MISO模型，通过设置模型端部不同的约束条件来模拟试件端部摩擦力无限大和无摩擦约束两种情况下混凝土压缩响应特征。

1 研究思路及主要流程

1.1 研究思路

在混凝土非线性有限元分析中，MISO模型和Druck-Prager模型是应用最为广泛的两种本构模型，且两者均与相应的强度准则（为理想塑性模型，屈服强度即破坏强度，故在此不作区分）相匹配。MISO模型遵循Mises强度准则，即材料破坏主要与其属性和应力偏量第二不变量J2有关，且其应力—应变关系通过多段线性关系给定。Druck-Prager模型将材料视为理想塑性体，材料的塑性破坏由其粘聚力、内摩擦角、剪胀角、J2和应力张量第一不变量I1共同确定，因而在一定程度上可以反映材料在静水压力作用下的破坏行为。

本次研究分别基于MISO和Druck-Prager模型模拟文献[5]中水灰比为0.4的饱和素混凝土三轴压缩试验，并综合对比模拟结果与试验结果。此外，进一步采用MISO模型对不同端部约束条件的影响进行探究，具体包括：（1）仅约束模型底部环向位移与竖向位移，以模拟压缩过程中试件端部不存在摩擦力的情况；（2）设置模型底部为固定端，同时约束模型顶部水平方向位移，以模拟压缩过程中试件端部摩擦力无限大的情况。通过模拟上述两种极端约束条件，在一定程度上可以反映试件端部摩擦力变化对混凝土三轴压缩行为的影响。

1.2 混凝土试件有限元模型构建

依据文献[5]，在ANSYS中构建混凝土试件有限元模型，其为圆柱形，高115 mm（z轴方向），直径54 mm。采用软件内置的65号实体单元（solid 65）及Concrete材料模拟混凝土，其依据Willam-Warnke（W-W）破坏准则判定混凝土压碎和开裂[8]。同时，为提升计算效率，加快收敛，本次研究中不考虑混凝土单元的压碎破坏，但需考虑混凝土压碎后的应力释放。混凝土试件几何模型（见图1）构建完成后，采用扫略方式对其体网格进行划分，网格尺寸为3 mm。混凝土试件有限元模型基本信息及材料参数见表1。

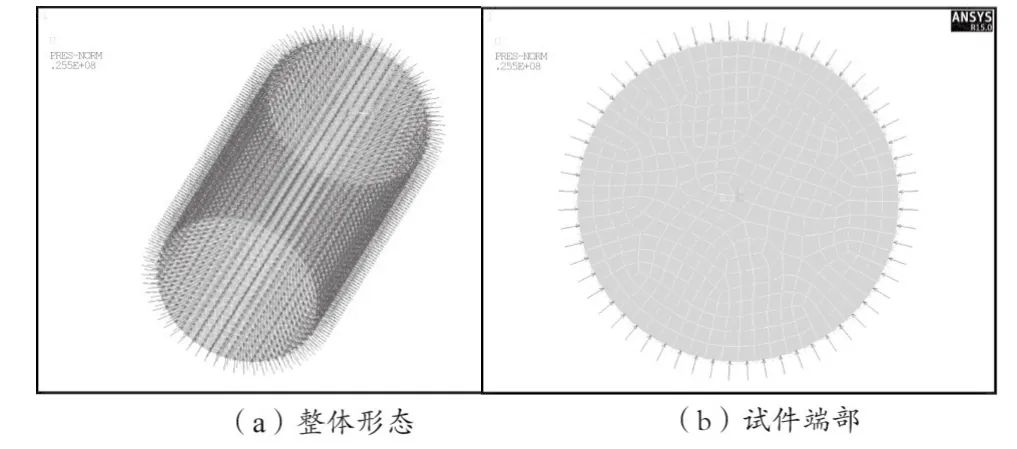
图1 混凝土试件有限元模型

表1中，混凝土试件fc和ν取值与文献[5]中一致。鉴于文献[5]中没有给出混凝土相应的ft，故根据式（1）进行估算[9]。fcb，f1，f2，c，φ由于缺乏试验数据，故根据混凝土单轴抗压强度及抗拉强度按式（2）～（8）换算[2]。张开裂缝的剪力传递系数及闭合裂缝的剪力传递系数根据文献[2]确定。在此需特别说明，尽管文献[5]中给出了饱和素混凝土单轴压缩应力—应变曲线，但相关图件清晰度有限，无法将实测应力—应变曲线精确定量化，故MISO模型中的应力—应变曲线上升段按Hognestad曲线方程[1]（式（9））确定，且将曲线下降段简化处理为一条水平线，即认为混凝土为理想塑性材料。因此，MISO模型中混凝土E0由fc和ε0确定，其值大于试验所测E0。而在Druck-Prager模型中，E0作为独立变量输入，故可采用实测E0值。

其中：β—混凝土材料常数；σy—混凝土屈服强度（MPa）；σc—混凝土应力（MPa）；εc—混凝土应变。

1.3 本构模型与边界条件设置

本次研究采用Druck-Prager模型及MISO模型进行模拟，并综合对比其模拟结果。MISO模型将应力—应变曲线划分为多个线性段。如§2.2所述，各线性段的应力—应变关系由Hognestad曲线方程确定。在Druck-Prager模型中，应力—应变关系通过给定的材料常数即可确定，其规定在屈服强度之前服从线弹性应力—应变关系，屈服强度之后则为理想塑性。

表1 混凝土试件有限元模型基本信息及材料参数

模拟过程中，首先采用应力边界条件在模型侧表面施加拟定围压（分别为0，25.5和51.2 MPa），待求解平衡后，在模型顶部施加位移边界条件（沿z轴负方向位移为1～10 mm）以模拟压缩加载。此外，模型顶面及底面约束条件详见表2。

表2 混凝土试件有限元模型顶面及底面约束条件

1.4 模拟结果后处理

本次研究主要对模型轴向应变、体应变及轴向应力间的关系展开分析，并与Imran的研究结果进行对比。其中，模型体应变和轴向应变可采用AN⁃SYS内置后处理模块进行提取。但由于模拟中采用位移边界条件进行轴向加载，故采用命令流提取模型顶面各节点反力的合力，并将该合力与模型顶面面积之比作为所施加的轴向应力（σa）。

此外，鉴于文献[5]中采用电阻式应变片量测混凝土柱中间部位的表面应变，故本次研究亦提取混凝土试件有限元模型中间部位单元的侧向应变，并采用与文献[5]相同的计算方式（式（10））求取体应变。

式中：εV—体应变；εa—轴向应变；εL—侧向应变。本次研究中规定以拉伸为正、压缩为负。相应地，试件体积膨胀（剪胀）为正，试件体积缩小（剪缩）为负。

2 结果分析

2.1 不同本构模型模拟结果对比分析

本节模拟均采用A类约束条件（不考虑端部摩擦），基于Druck-Prager模型和MISO模型得到的σaεa曲线与εV-εa曲线分别如图2和图3所示。结果表明模拟结果与试验结果总体变化趋势基本一致，但在具体数值上存在较大偏差。表3列出了各围压条件下混凝土试件峰值强度σpeak以及峰值强度对应的轴向应变εpeak与割线模量Es的实测值和模拟值。

就峰值强度而言，无侧限条件下两种模型模拟结果与实测结果较为接近。当围压增大，两种模型的模拟结果均偏离试验结果。其中，MISO模型模拟出的应力—应变关系较为保守。相反，Druck-Prag⁃er模型则严重高估了混凝土试件抗压强度，其在51.2 MPa围压条件下的抗压强度模拟值高达983.09 MPa。Druck-Prager模型的强度准则考虑了静水压力作用，且认为混凝土破坏之前处于线弹性状态，其或许是导致试件在高围压条件下模拟抗压强度显著提升的原因。此外，εpeak的实测值和模拟值均随围压增大而减小，反映出围压对混凝土变形的约束作用，即随围压增大，混凝土延性增强。然而，MISO模型所得εpeak值随围压变化并不显著，其与试验结果差异较大。同时，Es的模拟值普遍比实测值大，且两者随围压变化规律相反，即Es实测值衰减幅度较大。其原因在于本文采用的MISO模型和Druck-Prager模型均为理想塑性模型，且应力—应变曲线上升段斜率变化较小，所以无法反映出混凝土弹性模量的快速衰减。在此亦需强调，由于模拟采用的本构模型不含下降段，故模拟结果无法反映混凝土的应变软化行为。

图2 轴向应力σa与轴向应变εa关系曲线

图3 体应变εV与轴向应变εa关系曲线

表3 混凝土试件峰值强度、峰值强度对应的轴向应变与割线模量模拟值和实测值

就体应变—轴向应变关系而言，Druck-Prager模型的模拟结果显著优于MISO模型。相较实测曲线，Druck-Prager模型模拟结果夸大了混凝土剪缩程度，高估了裂缝产生时的轴向应变，该现象在低围压条件下尤为显著[图3（c）中加粗线段为趋势延长线，并非模拟结果]。MISO的模拟结果则与实际相悖：（1）一方面，随围压增大，混凝土模型剪缩程度减小；（2）另一方面，模型剪缩程度对围压改变极不敏感，且体变值极小，表明压缩未导致混凝土内部裂隙显著发育。MISO模型模拟结果与试验结果的差异可能与模型端部约束条件有关，即三轴试验中混凝土试件端部与加压板之间存在摩擦力，其会显著影响混凝土变形破坏特征，故拟基于MISO模型对端部约束条件影响进行探究。同时，鉴于Druck-Prager模型严重高估混凝土强度，并兼顾计算效率，在此不再基于Druck-Prager模型分析端部约束条件影响。

2.2 不同端部约束条件模拟结果对比分析

在前文基础上，本节采用B类约束条件（端部摩擦无限大）进行模拟，最终得到的σa-εa曲线与εV-εa曲线如图4和5所示。

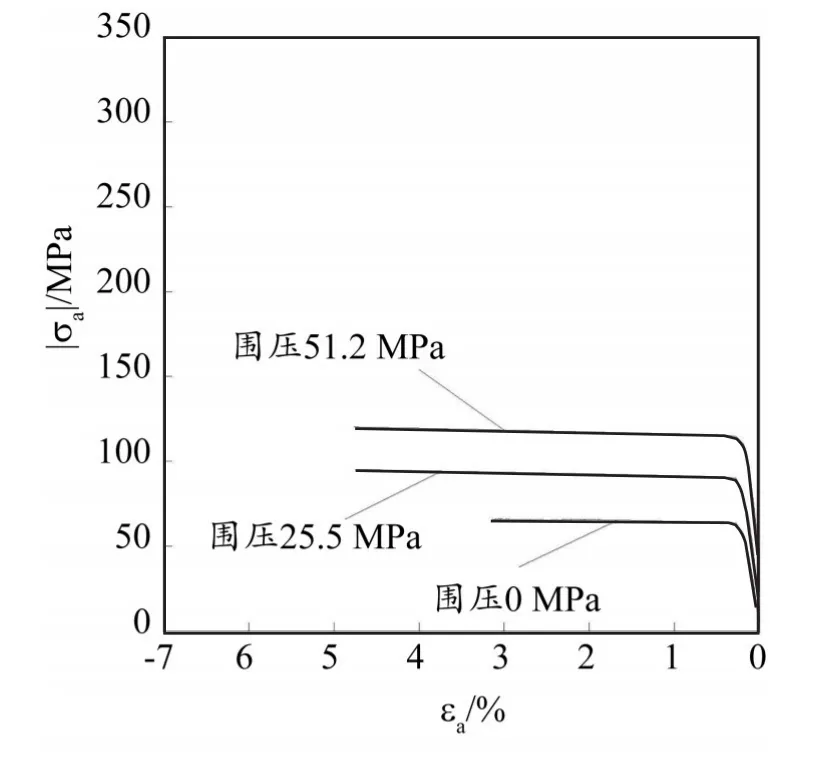
图4 B类约束条件下轴向应力σa与轴向应变εa关系曲线

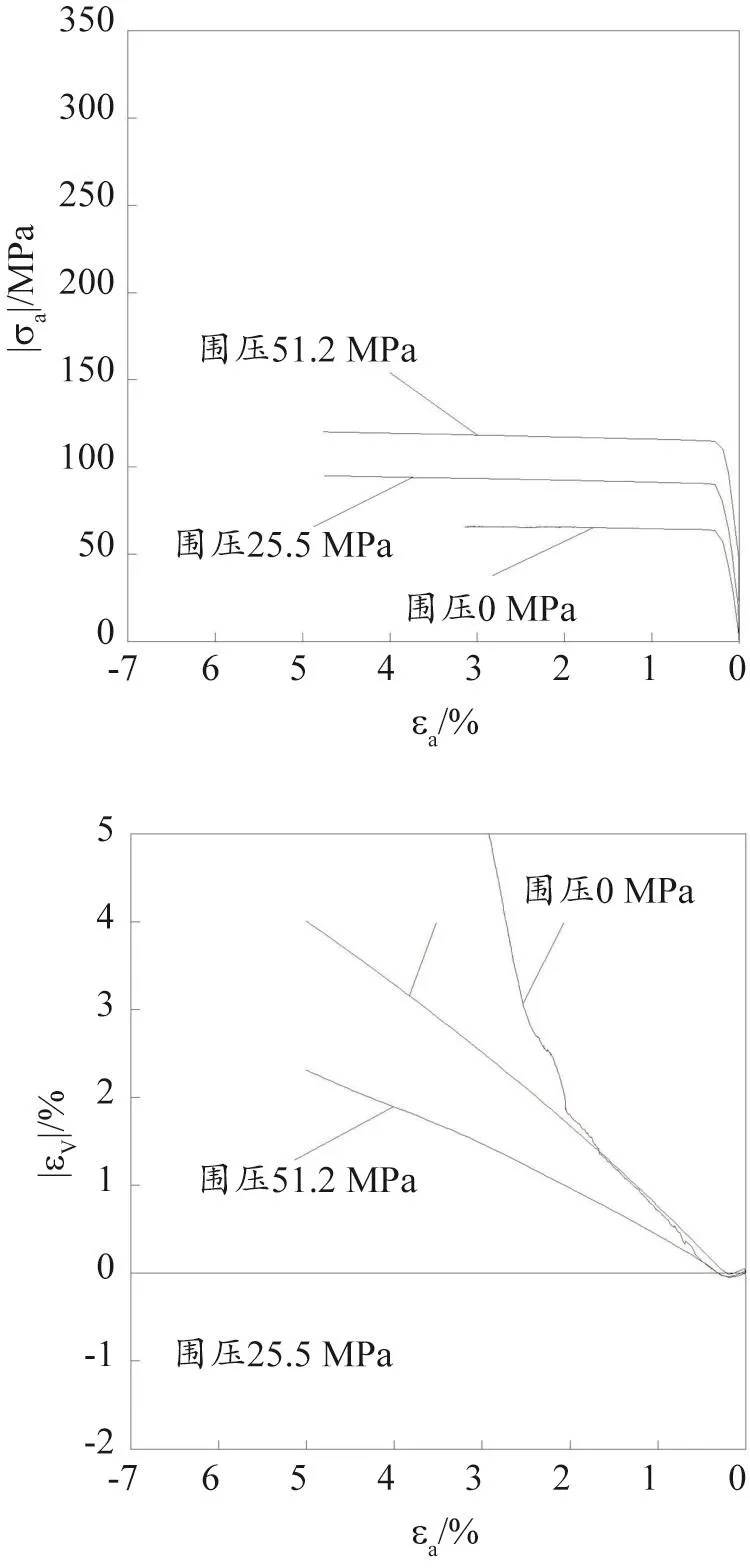
图5 B类约束条件下体应变εV与轴向应变εa关系曲线

图4和5表明，端部约束条件对混凝土应力—应变曲线无显著影响，但会改变混凝土体变特征。相较图3（b），当约束模型端部水平位移时，混凝土发生明显的剪胀，即端部摩擦约束加剧混凝土内部结构损伤。然而，与实测混凝土体变特征相比，B类约束条件下MISO模型的模拟结果仍有较大缺陷，包括：（1）混凝土在压缩初始阶段的剪缩效应未能体现；（2）体变响应对围压的敏感性仍未能凸显。