一种人体运动机能非线性评价指标研究

张 霞,傅 豪,胡晋嘉,陈仁祥

(重庆交通大学 机电与车辆工程学院， 重庆 400074)

穿戴式机器人运动辅助过程中，通过获取人体运动信息并有效识别出人体运动机能，有利于穿戴式机器人主/从运动控制的研究，为提高机器人的柔顺运动辅助控制提供理论支撑[1]。根据研究方向不同，人体运动信息可分为4种：第一种是人体运动姿态的描述；第二种是描述人体运动时的力学参数，如受力情况、人体质心和速度等参数；第三种是人体运动时的生理信息，比如人体运动时肌肉收缩、放松变化产生的肌电信息；第四种是利用信息融合技术宏观描述人体运动的协调性、平衡性等。由于表面肌电(surface electromyography，sEMG)信号变化与肌肉活动功能状态之间存在良好的相关性，同时sEMG信号的获取与分析也具有实时性、客观性、敏感性和灵活性等特点[2]，因此在人体运动信息相关研究中，肌电信号具有天然的优势。

根据研究对象和应用领域的不同，sEMG信号的研究主要分为三类：第一类是人的肢体动作的识别，该方法通过提取特征参数结合机器学习的算法对动作模式进行分类，达到识别人体动作的目的，广泛应用于残疾人的假肢控制领域[3-5]；第二类是肌肉疲劳及肌力的评价与判断，sEMG信号的幅值一般和肌肉运动力度成正比，可以通过sEMG信号对肌力进行估算，文献[6-8]利用信号的时频分析技术，对递增负荷下肌肉周期性动态疲劳进行估计，文献[9]利用曲线拟合的方法建立了肌力预测模型，并考虑了疲劳状态下的肌力；第三类是疾病机理的研究以及康复治疗，例如对脑卒中、疼痛症等疾病的分析，陈文敏、宋红梅等[10-11]讨论了身体疼痛与sEMG信号特征之间的关系。上述文献表明：目前sEMG信号分析手段主要集中于时、频域分析，时域特征指标有积分肌电值(integral Electromyographic，iEMG)、均方根值(Root Mean Square，RMS)和平均振幅(Mean Amplitude，MA)；频域特征指标有平均功率频率(Mean Power Frequency，MPF)和中位频率(Median Frequency，MF)，普遍采用上述指标定性描述sEMG信号特征与肌肉疲劳与肌力状态之间的关系[2]。由于sEMG信号实则是大量运动单元生物电活动在时间和空间上的非线性耦合，其特征非常复杂。传统单一的评价指标与分析技术存在一定的局限性。因此迫切需要采用非线性分析的方法与技术开展sEMG信号非线性特征与运动机能状态的相关性研究，进而挖掘出一种能有效评价运动机能的指标。

本文提出了一种基于分形维数标准差的人体运动机能非线性评价指标，采集人体下肢正常步行的sEMG信号进行预处理，再采用相空间重构和最大李雅普诺夫指数分析的方法，确定sEMG信号是一种混沌信号，进而采用计算分形维数的方法表征与运动机能密切相关的sEMG信号的复杂度，并提出分形维数标准差的评价指标用于评价持续运动过程中肌肉收缩、放松能力。通过对比分析运动能力存在差异的测试者的实验数据，证明分形维数标准差的运动机能评价指标能够有效表征不同个体的运动机能强弱，对穿戴式机器人的柔性运动控制提供理论依据。

1 sEMG信号采集与预处理

1.1 实验设备

采用可穿戴式sEMG测量装置Due-Pro进行肌电信号采集，其外观如图1所示。该设备有8个无线探头最多可采集14个sEMG信号以及2个辅助信号(例如力、角度)，通过蓝牙通信进行数据传输，并通过Matlab脚本程序进行数据保存供后期的数据处理。

图1 Due-Pro采集装置

1.2 实验方案及信号预处理

本文选择5名运动机能存在强弱差异、年龄为20～25岁且下肢步行正常的受试者，其中男性3名，爱好体育运动并有运动习惯；女性2名，没有运动习惯，可以假设男、女测试者之间运动机能存在差异。设定受试者在运行速度为3 km/h的跑步机上步行，采集下肢右腿股直肌、股外侧肌、股内侧肌等八块肌肉的sEMG信号。步行时长60 min，每间隔5 min采集1次信号，每帧时长1 min，采样频率为2 048 Hz，信号采集场景如图2所示。

图2 信号采集场景

采用中值滤波和带通滤波的方法对sEMG信号进行预处理，滤波后各肌肉的sEMG信号如图3所示。中值滤波中模板长度设为100，带通滤波参数为通带左边界20 Hz、通带右边界50 Hz、衰减截止左边界1 Hz、衰减截止右边界500 Hz。

图3 滤波后的sEMG信号场景图

2 sEMG信号的非线性分析

2.1 sEMG信号的混沌性质

本文采用坐标延迟法对sEMG信号进行相空间重构，即根据时间序列{x(i)∶i=1,…,n}的不同延迟时间τ来确定维相空间空间矢量y(i)，矢量y(i)可表示为

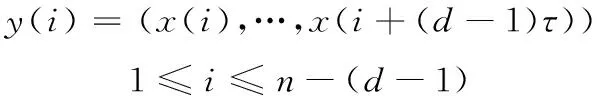
(1)

采用交互信息法计算τ，计算流程如下：

定义(S,Q)=(x(i),x(i+τ)),1≤i≤n-τ，也即S代表序列x(i)，Q代表序列x(i+τ)。则交互信息量I(S,Q)是关于延迟时间τ的函数，也记作I(τ)，I(τ)可表示为：

I(τ)=I(S,Q)=H(S)+H(Q)-H(S,Q)

(2)

式中H(S)与H(Q)分别为S与Q的熵，H(S,Q)为(S,Q)的共熵。计算出交互信息曲线I(τ)=I(S,Q)第一次达到极小值时的延迟时间就是最佳延迟时间，本文取延迟时间τ=16。

采用虚假最临近点法计算嵌入维数d，即从最小嵌入维数2逐渐增加维数d，计算出处于当前维数下的虚假最临近点所占比例，直到比例小于5%或者随着维数的增加虚假最临近点不再减小的时候，此时的维数就是嵌入维数，本文取嵌入维数d=2。

为了探讨肌电信号是否为混沌信号，利用上述方法对sEMG信号、标准正弦周期信号及取值在[-1，1]的随机信号进行相空间重构，计算结果如图4所示。

图4(a)、图4(b)、图4(c)分别显示了sEMG信号、随机信号和周期信号的相空间重构图。区别于周期信号及随机信号，sEMG信号的运动始终限于有限区域，轨迹永不重复并且形态复杂，其运动的复杂程度介于周期信号和随机信号之间。这说明sEMG信号中的不稳定因素驱使状态轨迹无限延伸，状态轨迹在相空间中密集和遍历，而稳定因素又将状态轨迹限制在一定空间内，形成一定层次结构，具有明显的伸长与折叠变换特点，结果表明sEMG信号具有混沌吸引子的典型特征，是混沌信号。

图4 相空间重构图

非线性动力系统在其相空间中的稳定状态可以通过最大李雅普诺夫指数定量地描述出。本文再次通过计算最大李雅普诺夫指数来确定sEMG信号的混沌性，最大Lyapunov指数可由式(3)计算获得：

(3)

式(3)中，L(tk)表示tk时刻最邻近零点间的距离；M为计算总步数。不同的λmax对应于不同的运动状态，各种运动形式及其对应的最大李雅普诺夫指数如表1所示。

表1 各种信号最大李雅普诺夫指数

分别截取五名测试者的RF(股直肌)sEMG信号，按上述方法计算最大李雅普洛夫指数值分别为：0.032 9、0.025 4、0.027 3、0.059 3和0.037 2。对比表1，sEMG信号的最大李雅普诺夫指数都处于0～∞的区间以内。该结果亦证明了sEMG信号为混沌信号，与前述分析结果一致。

2.2 sEMG信号的复杂度特征分析

肌肉收缩时，运动单元集中放电，信号成分较单一；肌肉放松时运动单元随机放电，信号成分较复杂，因此，可认为sEMG信号复杂度与运动机能密切相关。本文采用计算分形维数的方法分析sEMG信号的复杂度特征，即利用分形维数表征信号的复杂度。采用“覆盖分维”的思路计算sEMG信号的分形维数。由“覆盖分维”定义，用大小为的盒子取覆盖分形曲线，盖完所必需的最少盒子数目为N(ε),计算分形维数D的公式如下：

(4)

为了证明分形维度与信号复杂度的相关性，本文通过合成不同占比的周期信号与随机信号形成多个耦合信号，其中每一帧信号长度相同，利用上述方法逐个求取各耦合信号的分形维数，其结果如图5所示。

图5 不同信号对应的分形维数曲线

图5的结果表明：耦合信号中的周期信号占比越大，随机信号占比越小，信号中的复杂成分就越少，分形维数越小，反之。周期信号的占比趋近于100%时，信号的分形维数值趋近于1。因此可以得出分形维数越小，信号复杂度也就越小；反之，信号复杂度越大，分形维数与信号复杂度呈正相关。

表2为sEMG信号、周期信号、随机信号的分形维数。周期信号的分形维数最小，其值趋近于1，信号的复杂度也最小；随机信号的分形维数最大，信号的复杂度也是最大。而sEMG信号的分形维数介于周期信号与随机信号之间，该结果说明采用分形维数表征信号复杂度的可行性。

表2 sEMG、周期、随机信号的分形维数

2.3 分形维数标准差非线性指标

采用上述分形维数的计算方法计算下肢8块肌肉的sEMG信号分形维数，研究了8块肌肉的sEMG信号分形维数随运动时间的变化规律。为了缩短计算时间并确保数据的可靠性，从步行运动5 min开始，每隔5 min分别截取5个步行周期、10个步行周期和15个步行周期的sEMG信号进行分形维数计算，其结果如图6所示。

图6显示了在一个小时的步行运动过程中，各块肌肉的sEMG信号分形维数的变化趋势。从整体来看，各块肌肉的分形维数随着运动时间的增长并没有明显的变化。同时，从图中可以看出5个步行周期、10个步行周期和15个步行周期的分形维数变化趋势基本一致，反映出步行运动中的sEMG信号分形维数变化比较平缓，由此可见分形维数反映了人体固有运动机能特征，与运动时间及肌肉疲劳无关。

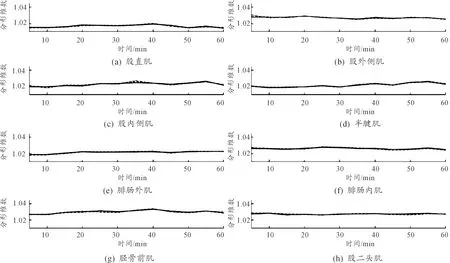
图6 分形维数随运动时间的变化趋势曲线

本文分别计算某一受试者肌肉收缩和放松时的分形维数，原始sEMG信号及其分形维数如图7所示。图7(a)代表sEMG信号，图7(b)代表sEMG信号对应的分形维数。

图7 肌肉收缩和放松的分形维数曲线

从图7可以看出：当肌肉收缩时sEMG信号的分形维数变小，信号的复杂度低；放松时分形维数变大，信号复杂度高，这是由于肌肉放松时肌肉纤维随机放电，肌肉收缩时肌肉纤维协同放电。并且人体肌肉的收缩能力越强，肌纤维放电越集中，收缩时的sEMG信号成分也越单一；而当肌肉放松时候则恰恰相反，肌肉的放松能力越强，放松时的sEMG信号成分越复杂。本文进一步统计了5名受试者肌肉静态收缩-放松时的sEMG信号分形维数，其结果如表3所示。表3结果表明，所有测试者在肌肉收缩时，分形维数较小，而在肌肉放松时，分形维数较大。总而言之，人体运动机能越强，其放松时sEMG信号分形维数越大而收缩时sEMG信号的分形维数越小。该研究结果表明测试者个体肌肉收缩-放松能力与收缩-放松时sEMG信号的分形维数差值有关。

表3 5名受试者肌肉静态收缩、放松的分形维数

为了评价持续运动过程中肌肉收缩-放松能力，本文进一步取数个周期sEMG信号分形维数的标准差，基于上述分析结果，假设分形维数的标准差越大，则肌肉收缩-放松时sEMG信号分形维数变化差异越大，肌肉收缩-放松的能力也就越强，运动机能越强。

进一步对比分析了2对4名测试者的数据。各测试者股直肌sEMG信号及其分形维数曲线如图8所示。从图8可以看出：男性测试者的肌肉收缩更加快速集中，sEMG信号整体表现出的肌肉收缩、放松规律也更强。计算出男性测试者1、2的分形维数标准差分别为0.010 7、0.008 5，女性测试者1、2的分形维数标准差分别为0.007 7、0.005 1。男性测试者的分形维数标准差比女性测试者的分形维数标准差大，则男性测试者的股直肌收缩-放松能力比女性测试者强，因此男性测试者运动机能比女性测试者强。

进一步对比分析5名测试者8块肌肉在持续运动下的数据，各肌肉sEMG信号的分形维数标准差如图9所示。从图9可以得出：同一块肌肉不同测试者的分形维数标准差存在大小差异，则不同测试者的同一块肌肉运动机能也存在强弱差异。该结果表明测试者个体肌肉收缩-放松时sEMG信号的分形维数标准差的差值与运动机能强弱有关。综上分析，本文所提出的分形维数标准差非线性指标能够有效评价不同个体的运动机能。

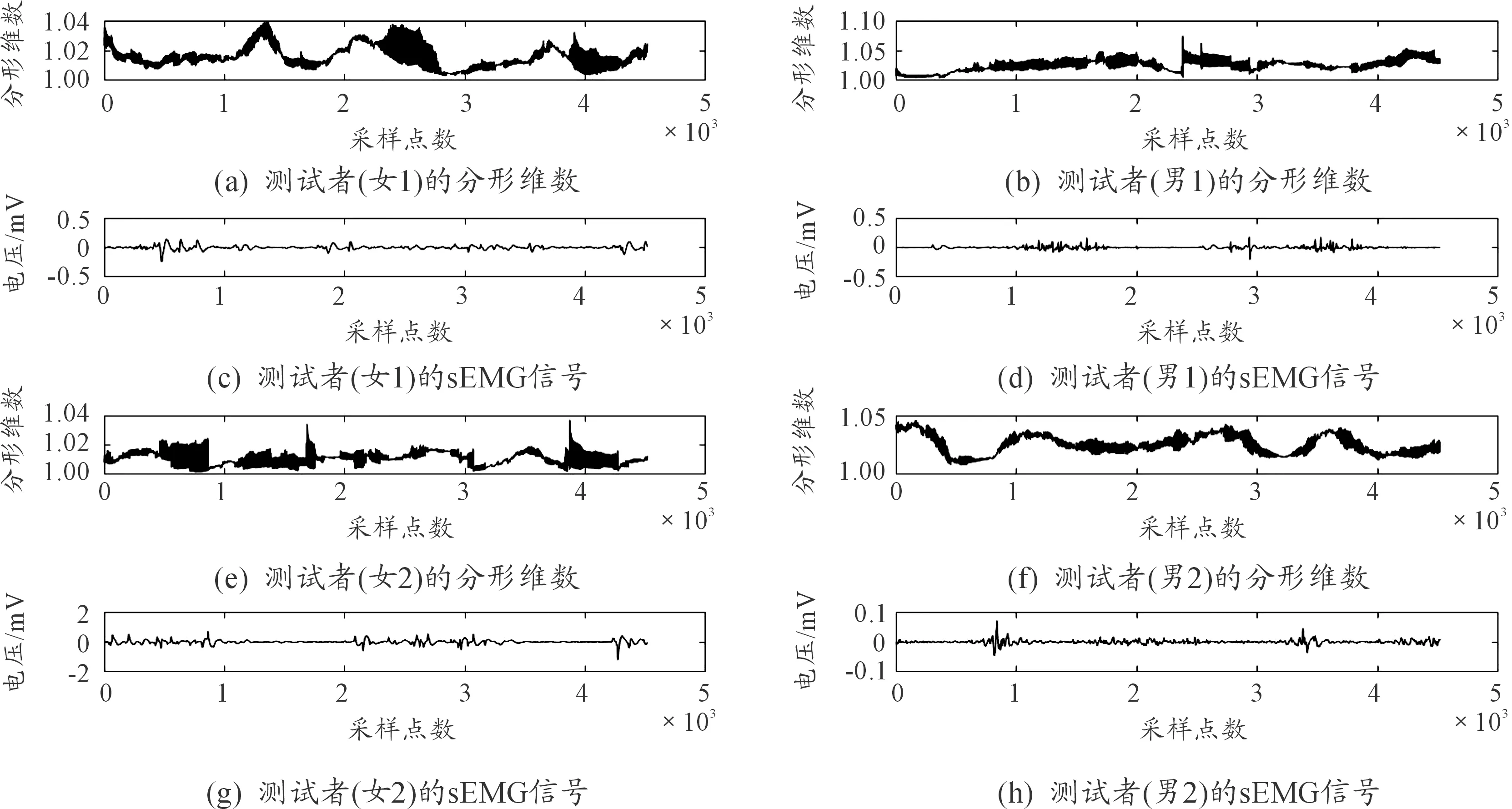
图8 不同受试者步行运动的sEMG信号及其分形维数曲线

图9 各肌肉分形维数标准差图

3 结论

对人体下肢正常步行的sEMG信号进行非线性分析，提出一种新的基于分形维数标准差的运动机能评价指标。采用相空间重构图和最大李雅普诺夫指数确定sEMG信号是一种混沌信号，由混沌信号的自相似性进而计算分形维数表征与运动机能密切相关的sEMG信号的复杂度，得出个体肌肉收缩-放松能力与其sEMG信号分形维数差值有关。为了评价人体在持续运动过程中肌肉收缩和放松能力，提出分形维数标准差非线性评价指标。通过对具有不同运动机能、共5位受试者的数据进行对比分析，证明分形维数标准差与肌肉收缩-放松能力的正相关性。本文提出的非线性指标能有效表征不同个体运动机能的强弱，可为穿戴式机器人的柔性运动控制实践提供理论依据。