“正方形半角”模型在中考压轴题中的应用

2020-09-06张杰

初中生世界·九年级 2020年8期

张杰

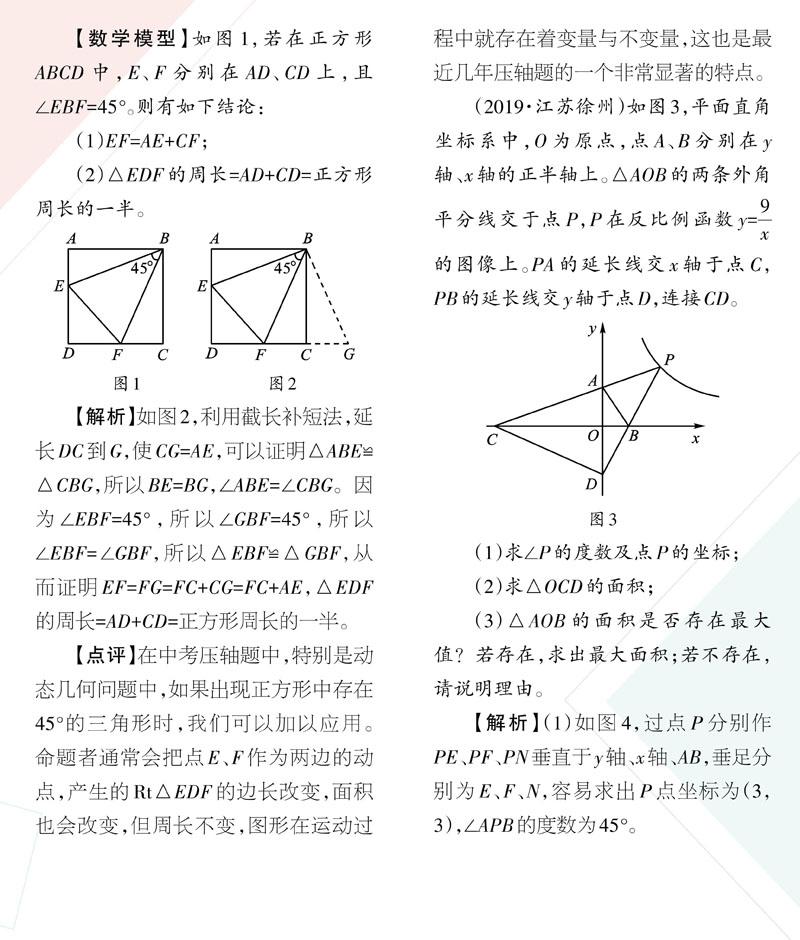
【数学模型】如图1，若在正方形ABCD中，E、F分别在AD、CD上，且∠EBF=45°。则有如下结论：

（1）EF=AE+CF;

（2）△EDF的周长=AD+CD=正方形周长的一半。

【解析】如图2，利用截长补短法，延长DC到G，使CG=AE，可以证明△ABE≌△CBG，所以BE=BG，∠ABE=∠CBG。因为∠EBF=45°，所以∠GBF=45°，所以∠EBF=∠GBF，所以△EBF≌△GBF，从而证明EF=FG=FC+CG=FC+AE，△EDF的周长=AD+CD=正方形周长的一半。

【点评】在中考压轴题中，特别是动态几何问题中，如果出现正方形中存在45°的三角形时，我们可以加以应用。命题者通常会把点E、F作为两边的动点，产生的Rt△EDF的边长改变，面积也会改变，但周长不变，图形在运动过程中就存在着变量与不变量，这也是最近几年压轴题的一个非常显著的特点。

（2019·江苏徐州）如图3，平面直角坐标系中，O为原点，点A、B分别在y轴、x轴的正半轴上。△AOB的两条外角平分线交于点P，P在反比例函数y=9x的图像上。PA的延长线交x轴于点C，PB的延长线交y轴于点D，连接CD。

（1）求∠P的度数及点P的坐标;

（2）求△OCD的面积;

（3）△AOB的面积是否存在最大值？若存在，求出最大面积;若不存在，请说明理由。

【解析】（1）如图4，过点P分别作PE、PF、PN垂直于y轴、x轴、AB，垂足分别为E、F、N，容易求出P点坐标为（3，3），∠APB的度数为45°。

（2）（解法1）如图5，连接OP，

∵∠APB=45°，∠POF=45°。

∴∠PCO=∠DPO，且∠POC=∠DOP=135°，

∴△PCO∽△DPO，

即CO·DO=PO2=（3

∴△COD的面积=9。

（解法2）设OA=a，OB=b，则AE=3-a，BF=3-b。根据正方形中45°三角形模型得AB=AE+BF，∴AB=6-a-b。

∵AB2=OA2+OB2，

【点评】解法1的巧妙在于利用相似关系求出CO与DO的乘积，技巧性比较强。但考试的时候，我们在很短的时间内难以想出这个思路。

解法2考虑到OA、OB长度可以改变，这样OC与OD的长度也会改变，△COD的形状随之发生改变，但面积是否改变要看OC与OD的乘积。我们通过把OC、OD用OA、OB表示，运用代数式的变形求出结果。利用“正方形半角”模型得AB=EA+FB，结合勾股定理构建相等关系是解决问题的关键。这样的思路比较简单，容易上手，好突破，也能为同学们高中的学习打下基础。

【解析】（3）（解法1）这里从“正方形半角”模型更容易入手。此问就转化成这样一个数学问题，当Rt△AOB的周长为一定值时，求它的面积的最大值。根据经验，我们猜想这个直角三角形为等腰直角三角形时面积最大。

如图6，过点P分别作PE、PF、PN垂直于y轴、x轴、AB，垂足分别为E、F、N。设OA=a，OB=b，

则AN=AE=3-a，BN=BF=3-b，∴AB=6-a-b，∴OA+OB+AB=6，

∴a+b+a2+b2=6，

∴2ab+2ab≤6，∴（2+2）ab≤6，

∴ab≤3（2-2），∴ab≤54-362，

∴S△AOB=12ab≤27-182，

∴△AOB的面積的最大值为27-182。（解法2）如图7，取AB的中点M，连接PM、OM，根据三角形三边的关系知OM≥OP-PM=32-PM。因为点P在△AOB的外角平分线上，点P到AB的距离为3，

PM的最小值为3，所以OM≥32-3，此时

AB≥62-6。因为S△AOB=S正方形PEOF-S△ABP-

S△APE-S△BPF，根据“正方形内45°三角形”

模型AB=AE+BF，且点P到AB的距离为