基于变刚度与力反馈的虚拟3D画笔触觉行为
2020-09-06黄磊侯增选李楠楠张迪靖苏金辉
黄磊,侯增选,李楠楠,张迪靖,苏金辉
(大连理工大学 机械工程学院,辽宁 大连 116024)
无论是从企业层面还是从普通消费者的层面来讲,产品外观设计阶段在工业零部件或消费产品的概念设计阶段都占有非常重要的位置.产品外观设计,包括产品形状设计和产品外表面的装饰,通常采用计算机辅助工业设计(Computer Aided Industrial Design,CAID)的手段或方式来完成.传统的CAID采用纹理映射的方法来实现从二维图片到三维模型外表面的转换,以此来实现3D 产品外表面的装饰[1].然而,从2D 图片到3D 物体外表面的映射变换很容易引起原有图形的扭曲和走样,并且纹理映射应用的过程既繁琐又易耗用过多的计算机内存资源.在产品的创新设计中,设计师的灵感非常重要,而纹理映射技术需要映射二维图形到三维物体的外表面,妨碍了设计师自由地捕捉设计灵感.伴随着虚拟绘画与书法的深入发展,尝试在3D 产品模型外表面直接进行虚拟装饰的方法开始被关注.该方法不仅能避免纹理映射存在的过度扭曲等一系列缺点,还能允许设计师完全自由发挥想象力和捕捉设计灵感.画笔是触觉虚拟绘制技术的主要实施工具,艺术家通过灵活控制画笔的位置、姿态、实时弯曲变形来完成产品创作过程.因此,在虚拟交互式的三维绘制过程中,能否构造出一个有表现力的基于物理的虚拟3D 画笔模型是非常重要的环节.
针对虚拟画笔建模及其绘制问题,国内外学者已做了大量研究,并取得了重要进展.Artnova 系统[2]采用了一种以用户为中心的观看技术,通过考虑用户的触觉操作,将视觉和触觉反馈集成起来,动态地确定新的视点位置.但在系统中并未构建3D 画笔模型,这也降低了交互式绘制体验的真实性.Gregory等[3]提供了一种直观的基于触觉设备的三维绘制接口,用于交互式的编辑和绘制多边形网格.系统通过视觉与触觉两种反馈能够让用户自然的创建出复杂的绘制模式.然而该系统并未集成6 自由度力反馈设备,并且在绘制过程中不能实现双手交互.Fu 等[4]提出了一种触觉绘制系统,该系统为用户提供一种简单的方式能精确地将颜色添加到网格模型上.该绘制系统还将虚拟画笔与一种配备了3 自由度的触觉设备集成起来.由于真实的画笔具有6 自由度,因此该系统不能提供给用户多种富有表现力的画笔效果.在虚拟画笔建模方面,Chu 等[5]提出了一种基于画笔笔画轮廓的建模方法,利用前后连接的贝塞尔曲线来实时模拟画笔笔道的形成.Kim 等[6-7]在原有画笔模型的基础上,通过添加画笔笔毛束的几何学模型及其相关变形算法,得到了一种新的画笔模型,该模型可以更好地模拟真实画笔的变形.Baxter[8]通过对原有画笔模型加以改进,并采用能量最小化的方法来优化画笔笔头的几何学表示.Larsson 等[9]提出了一种新型的画笔模型,该画笔几何模型用自由运动链表示画笔的中心脊骨,并利用多边形网格表示画笔中的笔毛簇,基于最小包围球思想并结合能量最优化理论求解画笔笔头的变形.徐军[10]于2017年在深入分析毛笔物理性能、归纳毛笔建模方法以及在总结毛笔笔法的基础上,通过分析力对毛笔变形的影响机理,采用弹簧-振子模型构建了毛笔力反馈仿真新模型,并根据毛笔受力后的形态变化和运动变化,研究了笔道绘制算法,实现了毛笔笔道的实时绘制.
基于上述研究,本文提出了一种新型的基于物理的变刚度3D 画笔模型以及相应的三维物体表面触觉绘制和装饰方法,并融入实时力反馈技术和采用一台6 自由度的力反馈设备,实现了三维物体表面的交互式绘制.在绘制时,画笔的力觉信息可以实时传输给力反馈设备,因此,用户可以通过反馈的触觉力,实时调整绘制结果以达到预期效果.
1 虚拟画笔建模
为了实现三维物体模型表面的触觉绘制装饰,构建一个富有表现力的虚拟3D 画笔模型是非常重要的.基于画笔的实际特性,我们构建了一个带有双层结构的3D 画笔模型[11-14],该模型融合了画笔外在的几何学特性和内在的动力学特性,可以模拟真实画笔的物理特性,满足虚拟三维物体表面自由绘制与装饰的需求.
1.1 几何学模型
画笔的几何学模型与其力学模型紧密关联.受Chu 等[5]画笔建模方法的启发,我们将几何学模型(图1)表示为一个骨架和一个经过蒙皮的表面.脊骨骨架用于处理画笔的常规弯曲变形.将骨架描述为前后连接的线段序列(也称脊骨段),并且从笔根部到笔尖部,单个脊骨段将变得越来越短.
假定画笔骨架被n+1 个节点P0,P1,…,Pn划分为n 个小段,P0为笔尖节点,Pn为笔根节点.线段Pi-1Pi的长度定义为Li.L1,L2,…,Ln构成一等差数列,其计算公式为[15-16]:
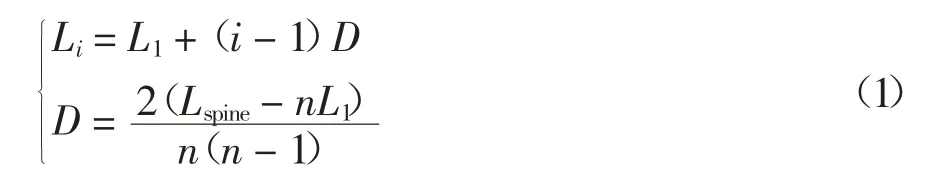
式中:i 是小于或等于n 的正整数;Li表示控制节点Pi和Pi+1之间的直线段(脊骨段)的长度;n 表示脊骨段的数量;L1的预设值与画笔笔头的硬度有关;D 表示公差;Lspine表示画笔骨架的初始长度.
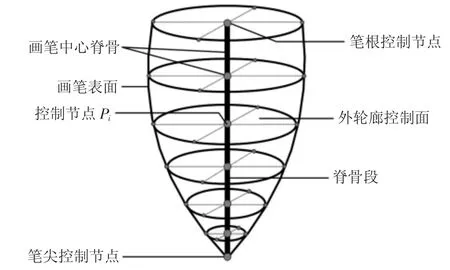
图1 画笔几何学模型示意图Fig.1 Sketch map of the geometric model of the brush
对于施加在画笔上的相同力,画笔笔头越软,则靠近笔尖处的鬃毛就越容易发生变形,此时L1的预设值就愈小,反之亦然.L1的值可以通过多次绘制实验获得.公差D 则由画笔骨架的初始长度(Lspine)以及L1的值联合决定.当画笔弯曲时,整个脊骨段位于同一平面内(图2).笔杆的倾斜角(即笔杆与绘制纸平面形成的角度)可表示为θ(θ∈(0,π)).而脊骨段Pi-1Pi与纸平面(虚拟投影平面)之间的夹角表示为αi(i∈[1,n]).如果画笔未发生弯曲,则αi=θ.在虚拟绘制过程中,不考虑画笔扭曲变形,弯曲的画笔中心骨架上所有的控制节点(P0,P1,…,Pn)都将处于同一空间平面上,该空间平面记为A0.为了约束画笔的变形,将一组横截面定义为画笔的轮廓控制面,此类横截面垂直于空间平面A0,同时穿过控制节点Pi,且平分于邻近的两个脊骨段所形成夹角.画笔表面被表示为三角网格面,该三角网格表面是由画笔中心骨架及一系列由上至下的轮廓控制面经过蒙皮操作而形成.当画笔未施加任何外力时,本文中的画笔形状类似于一个倒锥,因此画笔轮廓控制面在最初是一系列沿着画笔骨架方向放置的直径大小不同的圆.

图2 画笔骨架的变形Fig.2 The deformation of brush skeleton
在虚拟交互式绘制过程中,轮廓控制平面由圆变为椭圆.控制节点位置的变化引起中心骨架的变形,而每个轮廓控制面也将相应地发生位置和形状的变化,从而引起画笔三角网格面的变形.
1.2 画笔骨架弯曲力学模型
画笔力学模型构建的目的主要是用来仿真模拟绘制过程中画笔受到外来施加的弯矩和压力作用时的笔头弯曲变形、画笔笔头扁曲、笔毛散开等物理现象.
引入一种变刚度弹簧质量模型[17]来仿真绘制过程中当外力矩施加于画笔上的时候,画笔的动态弯曲变形(图3).
在虚拟交互式绘制过程中,将一个遵循空间平面内弯曲变形的虚拟扁截面变刚度的弹簧置于点Pm与接触点Pm′之间.这里,弯曲弹簧在虚拟绘制过程中将与绘制纸平面(或虚拟投影平面)成垂直或倾斜角度,并且虚拟弹簧与其在绘制平面内的正向投影(沿着法向量方向)形成一辅助空间平面Pk,受力的画笔将在空间平面Pk内发生弯曲变形.当画笔笔头刚开始接触到绘制平面时,笔头保持笔直状态.绘制过程中,随着在画笔笔杆端逐渐施加弯矩后,画笔中的可变刚度虚拟弹簧将开始产生弹性甚至弹塑性弯曲.此时,画笔骨架中的各脊骨节点的位置将跟随变化,同时规定各脊骨段的长度始终保持不变.
考虑实际圆画笔的形状特点,艺术家利用画笔实施书画创作时,经蘸墨后毛笔在外力矩的作用下与纸张接触并发生弯曲变形,由于连续地运笔动作,在纸面上形成各种笔道.基于上面的分析,我们可以得出画笔的力学模型可以用一个变截面变刚度的弯曲弹簧或者弯曲梁来描述(以下统一称之为弯曲梁),并且该弹簧在外力矩和纸面的共同作用下发生弹塑性弯曲变形.因此有必要深入研究该画笔笔头的复杂力学行为.
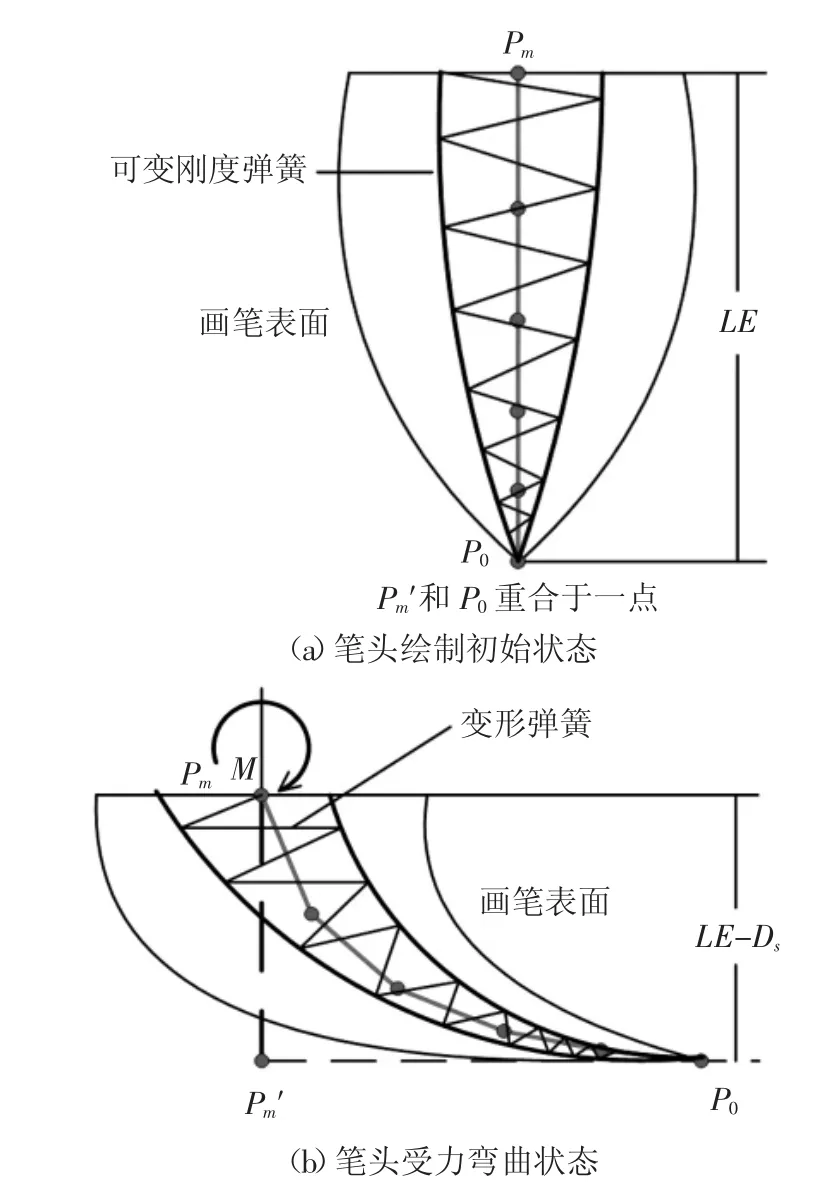
图3 带有可变刚度的画笔弹簧质量模型Fig.3 Brush spring-mass model with variable stiffness
1.2.1 画笔骨架弯曲变形的基本方程
首先我们可以将该弯曲弹簧抽象为一虚拟矩形变刚度悬臂梁,如图4 所示,其矩形截面的宽度沿着虚拟悬臂梁的长度方向保持不变,为常数b,矩形截面的高度沿着虚拟梁的长度方向不断变化,可用函数h(x)来表示.又规定虚拟梁的材料为理想的各向同性弹性材料.
为了降低计算的复杂度,规定虚拟梁受力弯曲变形属于平面内弯曲,不考虑扭转效应,那么其横截面沿着长度x 方向的高度函数及抗弯刚度函数分别为:
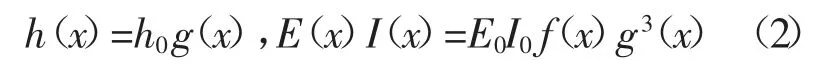
式中:h0和E0分别为常数,h0表示虚拟梁截面高度的参考值系数,E0则表示虚拟梁弹性模量的参考值系数:则表示虚拟梁横截面的惯性矩的参考值系数;f(x)和g(x)分别表示虚拟弯曲梁的弹性模量以及横截面高度方向沿着梁轴线方向的变化函数.
再假定,沿轴线方向的梁材料的屈服强度变化函数σs(x)为:

式中:σs0表示虚拟梁屈服强度的参考值系数;s(x)表示虚拟梁x 截面位置对Z 轴静矩.
当画笔骨架在受力弯曲的开始阶段,变形挠度不大,其内部的虚拟弯曲梁处于弹性变形阶段,对应的挠度we的微分方程为:

式中:M(x)表示虚拟梁横截面上的弯矩.
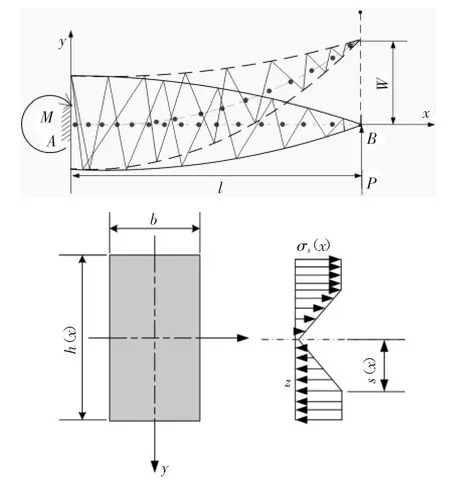
图4 可变刚度虚拟悬臂梁及其截面上弹塑性应力分布Fig.4 Variable stiffness beam with rectangular section and its elastic-plastic stress distribution
将式(4)实施两次积分,则得弹性区挠度积分公式为:
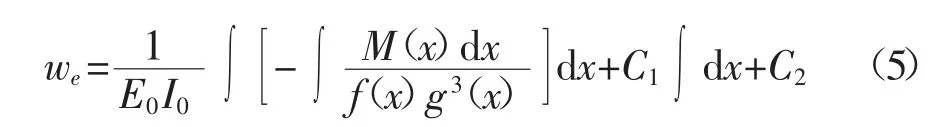
式中:C1及C2表示对应的积分常数,可由具体的虚拟梁两端的边界条件来确定.在虚拟绘制过程中,随着画笔骨架受力弯曲变形的进一步变大,伴随虚拟梁的横截面上的弯矩逐渐加大,当某一个横截面上最大的弯矩达到梁的弹性弯矩的极限Me(x)时,虚拟梁将进入弹性极限弯曲状态.Me(x)可通过下式计算得到(对于矩形截面梁).

下面,基于具体指定的虚拟梁截面高度函数、弹性模量变化函数,进行详细地虚拟变刚度弯曲梁(虚拟弯曲弹簧)的弹性弯曲变形分析.
1.2.2 弯曲骨架的弹塑性弯曲分析
本文将画笔骨架虚拟弯曲弹簧抽象为弹性模量函数为指数变化函数,而截面高度函数为线性函数的虚拟悬臂梁.首先,虚拟悬臂梁的截面高度遵循线性变化,沿着长度方向(也为梁的轴线方向)材料的的弹性模量遵循指数方式变化,即满足如下形式:

对于本文中的画笔力学模型,根据实际书写特点,可以将其力学模型抽象为左端固定右端自由的悬臂梁,忽略其自重,当在梁的自由端部施加一集中载荷P 后,可把式(7)(8)代入式(5)并做积分处理,则虚拟悬臂梁(本文中的虚拟弯曲弹簧)的挠度可以表示为:
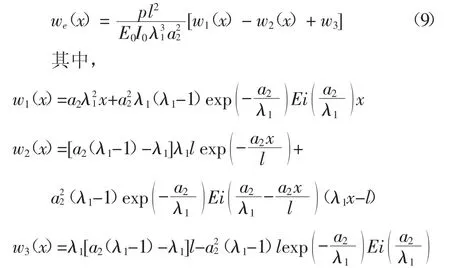
这里,Ei(z)代表指数积分函数.
1.2.3 力反馈分析
基于以上对画笔模型(可变刚度梁)变形的力学分析,可以建立一个能反映出画笔骨架弯曲变形与画笔实时受力之间的一一对应关系基本二维查询表,以期实现快速地力反馈计算,如表1 所示.

表1 反应画笔受力与相应的弯曲变形之间关系基本二维查询表Tab.1 Basic query table about the relation between the bending deformation and real-time force
表1 中,M 表示施加在笔杆处的弯矩;Pmb表示笔杆处截面的基本中心坐标,其初始值为(0,0,0);LE表示笔头的长度;P0b表示笔尖相对于点Pmb的基本坐标;θb表示笔尖处的截面法线相对于笔杆的相对转角;Pib表示第i 个画笔骨架节点相对于Pmb的基本坐标;θib表示在画笔骨架的第i 个骨架节点处的截面法线相对于笔杆的相对旋转角;mi表示施加在画笔骨架上第i 个骨架节点Pi处的弯矩.其中,M、Pmb、LE可由力反馈设备Phantom Desktop 实时提供,其余参数可由本文的算法求解获得.
基于上述基本查询表,可以得出许多重要的画笔受力变形参数.其基本思想被称之为“固定形状法”.固定形状法可以被分解为两步.
1)首先,考虑实际的画笔绘制过程,当施加于画笔的弯矩M、笔根中心节点Pm以及笔头长度LE一定时,则画笔骨架对应的弯曲变形形状就被固定下来了(而且无论当前画笔笔杆的实际姿态角是多少),如图5 所示.
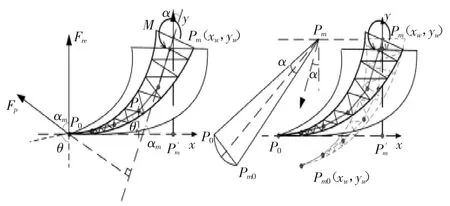
图5 画笔骨架的弯曲变形原理图Fig.5 The schematic diagram of the deformation of brush skeleton
因此,当画笔受力产生弯曲变形后,则“基本的”虚拟画笔笔尖点Pm0(xw,yw)的坐标(即相对于笔根中心点Pm(xm,ym))就是固定的,并且Pm0(xw,yw)可以通过使用基本查询表并参照Pm(xm,ym)的坐标值直接得到.
2)为了得到绘制时某一采样时刻笔尖点P0的实际坐标,可以假想将画笔骨架受力弯曲变形的基本形状Pm-Pm0以Pm(xm,ym)为圆心顺时针旋转α 角度(如图6 所示),此时辅助过渡笔尖点Pm0刚好落在水平x 轴上(即绘制平面上).相应地,点Pm0变换为实际绘制时的画笔笔尖点P0(xwa,ywa),且有ywa=0.基于图6 中的几何学知识,可以得到:

因此,xwa=xm-L,ywa=0.由角度转换关系,笔杆的姿态角经转换,其实刚好为α(图6 所示),它可由下式得到:


图6 画笔骨架受力变形分析原理示意图Fig.6 The simplified schematic diagram for deformation analysis of the brush skeleton
在笔尖节点处截面法线相对于竖直线(即绘制平面的法线)的绝对转角θ(如图5 所示)可由下式计算得到:

同理,参数Pi(表示画笔骨架上第i 个骨架节点的绝对坐标值)和参数θi(表示画笔骨架上第i 个节点相对于竖直线的绝对转角)都很容易通过计算得到(此处略去).由绘制平面施加给画笔笔尖部位的反力Fre(图6)可由下式计算得到:

式中:ξm是用于反力计算的调整因子,ξm∈[0,1],其可由多次绘制实验获得;Fp=(1+ξm)M/LE表示反馈力.
摩擦力可以使用户感知三维虚拟物体表面的粗糙,并能在绘制过程中稳定控制3D 画笔.摩擦力Ff可由下式计算得到:

式中:γ 是虚拟投影平面(虚拟绘制平面)的法向量与对应的三维物体表面法向量的夹角,且γ∈;μ 是摩擦系数,它可由多次实际绘制实验获得.
1.2.4 画笔表面变形
在实际绘制过程中,画笔笔头在压力的作用下开始与绘图平面接触并形成一个画笔笔触,笔头从笔根到笔尖部分逐渐变的扁平.因此,在绘制平面压力和摩擦力的作用下,画笔的每个轮廓控制面的形状将逐渐从圆形变为椭圆[14],如图7 所示.
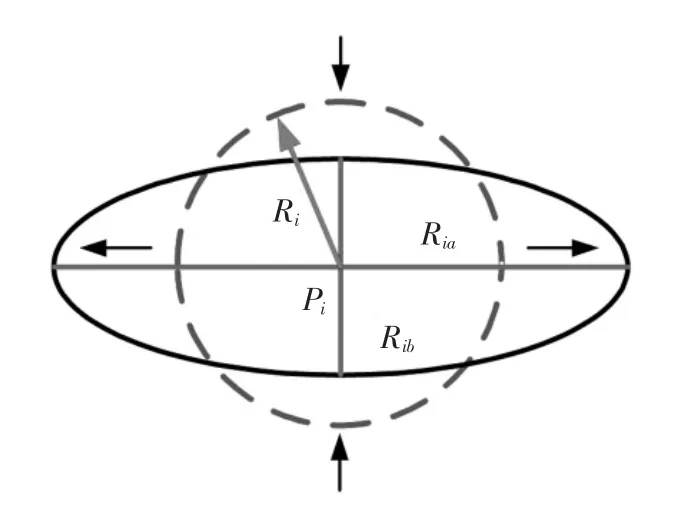
图7 轮廓控制面变形示意图Fig.7 Sketch of deformation of outline controlling surface
随着施加在画笔上压力的增加,椭圆的短轴Rib将越来越短,而长轴Ria将越来越长.因此,整个椭圆将变得更加扁平.当画笔未受到外力作用时,可以得到Ria=Rib=Ri.随着施加在画笔上的外力逐渐增加,椭圆的形状不断变化,Ria可由下式得到:
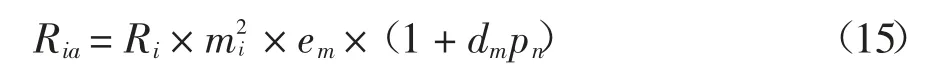
式中:mi是控制节点pi处截面的弯曲力矩;dm和em是通过实际绘制实验得到的椭圆调整因子,以模拟在不同的绘制条件下最真实的画笔变形;pn是压力系数,它被定义为压力F(绘制纸平面上的反力)与力反馈设备最大输出力的比值.这里,在我们的绘制系统中,所采用的力反馈设备Phantom Desktop 所能提供的最大输出力为7.9 N,因此pn=F/7.9,其pn∈[0,1],假定轮廓控制面的面积在变形前后保持不变,于是短轴Rib可由下式计算得到:

2 三维物体表面的虚拟绘制
在我们的绘制系统中,采用一种局部映射方法来实时地将二维画笔笔触映射到三维物体外表面.进而,通过沿绘制方向叠加3D 画笔笔触则可以得到3D 画笔笔道.然后,采用一种基于Kubelka-Munk 的颜色光学算法对3D 笔道进行实时渲染.
2.1 虚拟画笔二维笔触的形成
受Baxter 及Chu 等的启发,我们假定弯曲变形后的画笔笔头与虚拟绘制平面相交,将笔头穿透部分向绘制平面正向投影,则投影后的区域即为所形成的二维画笔笔触.该笔触轮廓可由经关键控制点插值后得到的两条对称的B-spline 曲线所组成,如图8(b)所示.在虚拟绘制过程中,可以通过控制笔触轮廓上关键点位置以及数量从而使二维笔触的形状与大小发生相应调整和变化.
基于几何学知识,线段Ni为虚拟绘制平面与画笔骨架上第i 个轮廓控制圆(圆心为Pi)相交得到.笔触轮廓控制点Md是变形的笔头的左侧轮廓线(图8(a))与毛笔骨架在绘制平面上的投影相交而得到,接着可以计算得到笔尖点P0的坐标值,根据P0进一步求得画笔中心骨架上节点Pi的坐标,进而可求得笔触轮廓控制点Ni、的坐标值,相关点的具体计算过程可参考文献[13].最后过以上关键轮廓控制点P0、Ni、、Md,并采用B 样条曲线插值法便可得到画笔的二维笔触轮廓,如图8(b)中所示.

图8 2D 笔触的生成Fig.8 The generation of 2D brush footprint
2.2 虚拟画笔与虚拟油泥3D 物体间的碰撞检测及接触力仿真
本文采用一种OBB(Oriented Bounding Box)包围盒算法[18-19],以实现虚拟画笔笔头与三维物体外表面之间的碰撞检测.为了确定画笔与三维物体(如虚拟油泥模型)之间的相对位置,引入了一个带有很小公差范围的参数-接触距离ddep.ddep被定义为画笔与虚拟油泥模型表面之间的距离.如果ddep处在给定的公差范围之内,系统将会产生一个很小的接触力(约0.1 N),并通过力反馈设备Phantom Desktop 传递给用户,从而虚拟画笔与虚拟3D 模型之间的接触可以快速地被用户所感知.
在系统中,虚拟画笔和虚拟三维模型的外表面被表示为三角网格,因此,ddep还可定义为笔尖P0与虚拟油泥3D 模型表面上一系列若干三角网格顶点之间的加权的平均距离.这些三角网格顶点十分靠近笔尖P0点,且其个数本文中默认值通常被设定为Mn=10.因此,ddep可由下式定量计算得到:

式中:wi为加权系数;ni为三维物体外表面的法向量;xi为三维物体表面三角网格顶点的坐标矢量;x 为笔尖节点P0的坐标矢量;di=;dmax为di的最大值.当ddep的值处在给定的容差范围内时,用户会感知到虚拟画笔与虚拟油泥3D 模型间的接触或碰撞.然后,用户可按下力反馈设备Phantom Desktop 上的触针按钮,可将接触力置为无效.然后,笔尖控制节点P0自动被系统约束到三维物体的表面,以便后续的触觉绘制仿真.笔尖P0的坐标矢量被变换为:

加权的平均矢量n 可表示为:

2.3 投影平面的确定
在虚拟三维绘制过程中,其中一个重要的环节就是如何建立合适的虚拟投影平面,该平面用于将二维笔触通过特定算法实时映射到三维物体的表面,从而形成对应的三维绘制笔触.受Larsson 等[9]关于最小边界包围球算法的启示,本文基于一种球扩展迭代操作建立笔头最小包围球.如图9 所示,顶点A 为受力变形后的虚拟画笔表任意一顶点,遍历整个虚拟画笔模型的表面顶点,搜索出距离顶点A 最远的画笔模型表面顶点B,同理,再搜索出距离顶点B 最远的画笔模型表面顶点C,以线段BC 的长度作为直径(其半径记为r0),BC 的中点D0作为球心,作球(D0,r0),并以此作为画笔笔头的初始边界包围球;顶点E 为初始边界包围球(D0,r0)之外的画笔上的一个顶点,我们将线段D0E 的长度表示为l1.过D0作D0E 的垂线并交包围球(D0,r0)于F、G 两点.连接EF、EG、FG,则三角形FEG 显然是基底为2r0的等腰三角形,FG 为包围球(D0,r0)的直径.然后在线段D0E 上取一点D1,连接D1F,并将D0D1的的长度记为ld1,将线段D1E 的长度记为r1.然后以r1为新的半径,以D1为圆形作新的扩展球(D1,r1).新得到的扩展球(D1,r1)的半径r1为:

线段D0D1的长度(ld1)为:

显然,基于几何学知识,很容易进一步计算得到扩展球(D1,r1)的中心坐标D1以及半径r1.重复执行以上步骤,直到变形的画笔笔头模型的所有外表面顶点都被涵盖在某一扩展包围球中,我们把此扩展球作为画笔笔头的目标最小边界包围球(Df,rf).
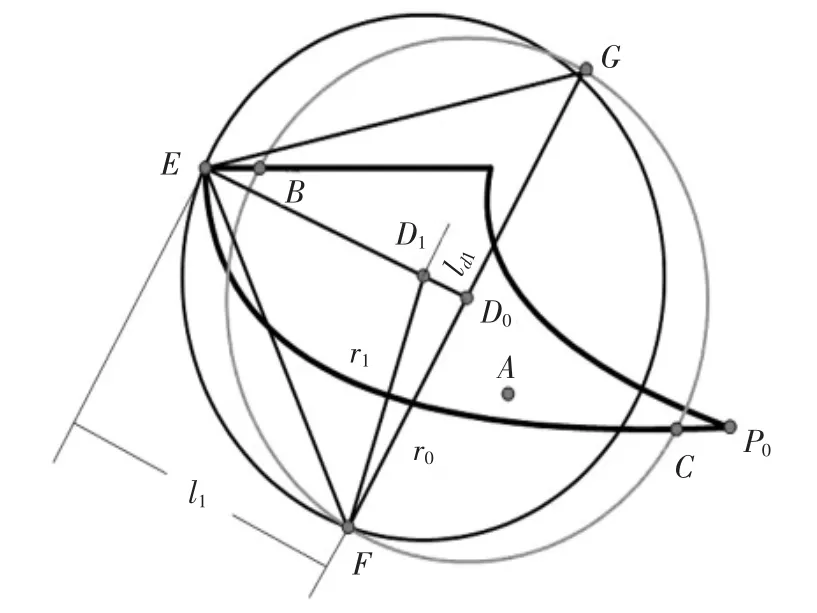
图9 弯曲画笔的包围球Fig.9 The bounding sphere of the bent brush
基于球扩展操作,得到了绘制笔头模型的最小包围球,在绘制过程中画笔笔根处的节点Pm在虚拟三维物体表面的投影点设为Pm′(如图10 所示),以最小包围球的球心Df为中心,搜索出距离点Df的长度小于等于rf的所有三维模型表面上的顶点,然后计算出这些顶点的各个法矢,我们取这些法矢的平均值作为待求的虚拟投影平面的法向量.同时又规定待求投影平面过点Pm′,经此操作,便确立了最终的虚拟投影平面位置.基于投影平面和画笔的弯曲变形,可以得到绘制过程中的二维画笔笔触,再将得到的二维笔触轮廓向三维模型表面反向投影,便可获得虚拟物体表面的三维笔触.
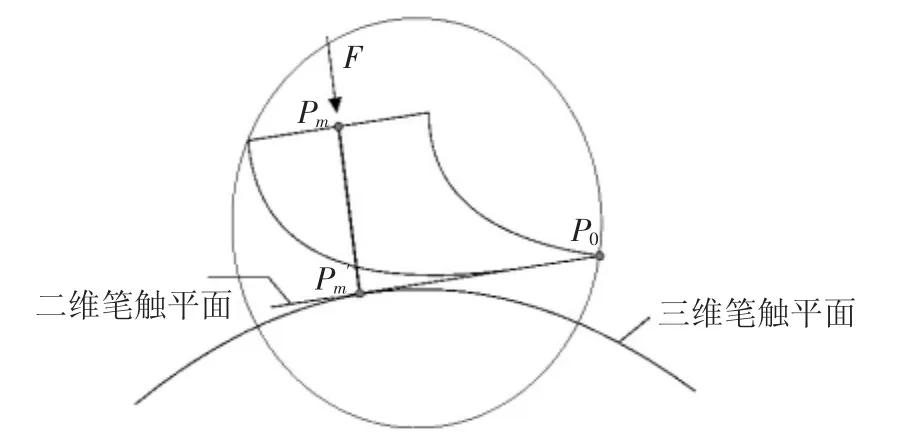
图10 二维画笔笔触平面的确定Fig.10 The determination of the 2D brush footprint plane
2.4 三维笔触水墨量及笔道的形成
在交互式的3D 笔道仿真过程中,含于笔头中的水墨实时的从画笔传输到与三维物体表面相接触的部分,并将计算后的墨量及颜色填充至相接触的区域.通常而言,在某一采样时刻3D 笔触中的墨量值正比于施加于画笔笔杆的弯矩、画笔笔头内在对应采样时刻所剩余水墨量.将画笔笔头在蘸墨后的起始包含的墨量表示为Z,在第i 个采样时刻对应的弯矩因子为Mei=Mi/(7.9×LE),那么在最开始第一个采样时刻点对应的3D 笔触中包含的水墨量值(Q1)可由下式计算得到:

式中:η 表示不同画笔的水墨量计算因子,该系数通过多次模拟实验获得,用于调整和控制虚拟绘制过程中的3D 笔触所包含的水墨量,真实再现3D 物体外表面与画笔头间的水墨传输过程.那么对应于第i个采样时刻点的3D 笔触中所包含的水墨量可通过下式计算得到:
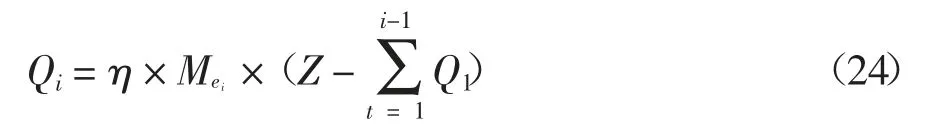
这里,i≥2,且i 取值为正整数.当画笔沿着某个笔划路径移动时,包含在画笔笔头中的墨水会被传输到三维模型的外表面.利用颜色光学KM 理论将油墨量转变为颜色强度值,于是在三维物体表面会形成带颜色的三维笔触.具体的原理如图11 所示.
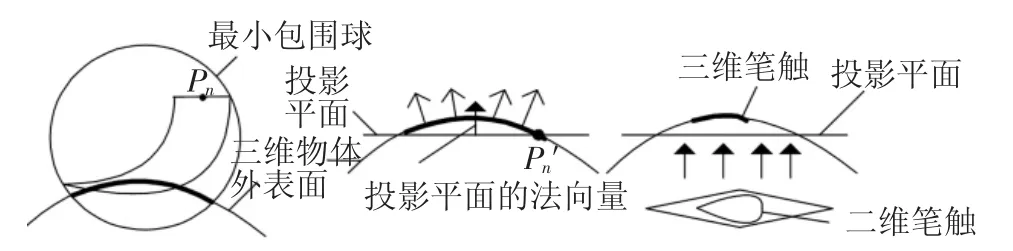
图11 映射2D 笔触以形成3D 笔触Fig.11 3D brush footprint formed by mapping 2D footprint
在虚拟3D 绘制过程中,通过沿采样点叠加3D画笔笔触可形成3D 画笔笔道(如图12 所示).
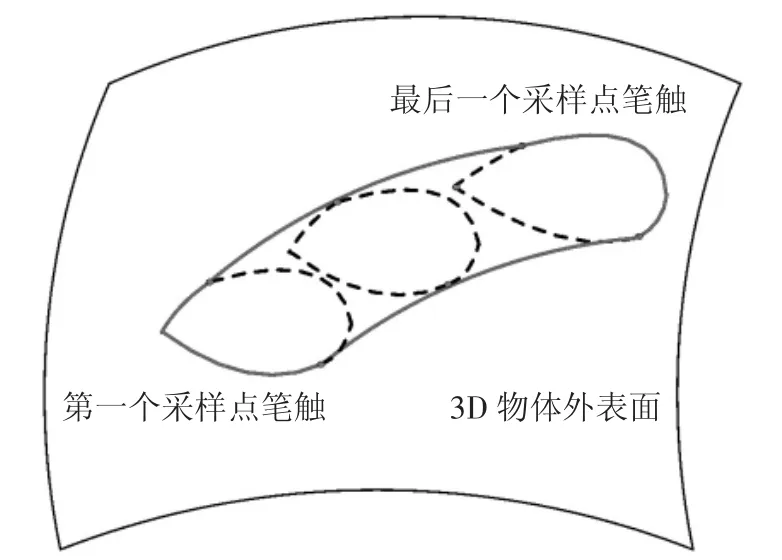
图12 叠加三维笔触所得到的3D 画笔笔道Fig.12 3D brush stroke formed by superimposing 3D footprints
2.5 画笔笔头分叉建模
在利用真实的画笔去实现诸如书法、绘画等艺术品的创作时,画笔的笔头分叉是一种奇特的绘制过程(物理现象),也是最难模拟的部分.基于实际绘制经验,观察得出笔头分叉与笔头所产生的弯曲变形量、画笔笔头的实时含墨量有关.当画笔笔头所产生的局部弯曲变形量以及实时含墨量达到某种阈值时,笔头的笔尖处开始出现分叉现象.在分叉模型中,距离笔尖处的局部骨架将由一个骨架分化成3个子骨架,每个子骨架又被脊骨节点分成若干个小脊骨段,每个子骨架的力学模型类似于上文中讲述的基本画笔骨架建模原理,如图13 所示.为了减少计算量,我们规定需要实现分叉的笔尖处局部骨架的长度约占整个画笔骨架长度的1/3.这里需要指出的是,画笔笔头的弯曲变形又和笔杆处所受到的弯矩M 成正相关.画笔笔头开始出现分叉时的阈值可用SP 表示,SP 可由下式求得:
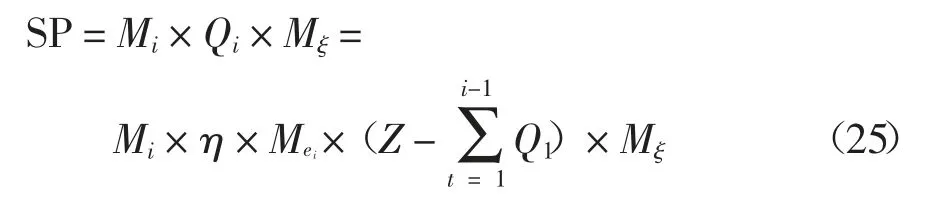
Mξ是分叉因子,由多次绘制实验获得.
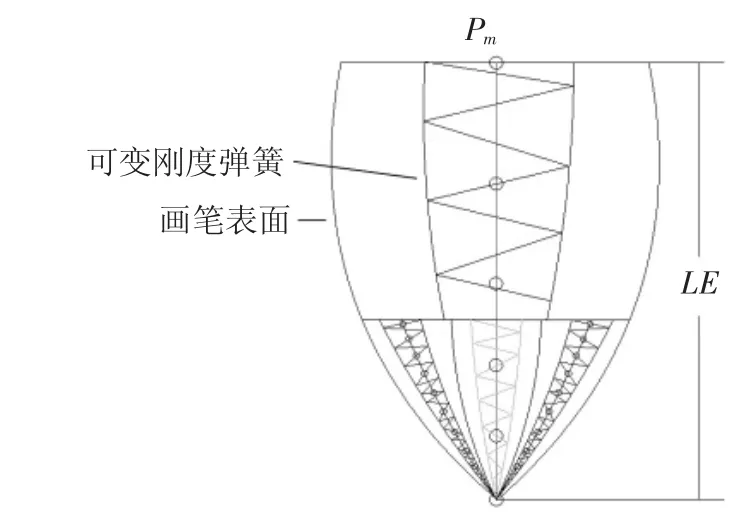
图13 画笔分叉示意图Fig.13 A schematic diagram for brush bifurcation
3 仿真实验验证
采用所提出的触觉画笔模型及虚拟三维绘制方法,成功开发出基于实时力反馈技术的虚拟三维绘制系统.该系统开发使用的主要编程语言为C++,使用的集成开发环境为vs2008,界面库采用QT,三维图形渲染库采用美国的商用图形开发包openinventor,触觉反馈库采用Sensible 公司的openhaptic 开发包,数学运算库采用科学计算库gsl.该三维绘制系统稳定运行于HP Xw8600 工作站上,并通过串行接口集成一台6 自由度的Phantom Desktop 力反馈设备(图14).力反馈设备可以实时提供画笔笔杆的受力和位置等相关信息,以用于计算画笔的实时弯曲变形和水墨传输过程.交互式触觉三维绘制系统界面如图15 所示.
第一个仿真实验内容是关于画笔受力变形问题,所采用的画笔参数如表2 所示.当对画笔施加不同的压力(Fre)时,所得到的相应画笔变形如图16 所示.可见画笔受力越大,弯曲变形越明显,同时得到的笔道也越宽.

图14 力反馈设备Phantom DesktopFig.14 The haptic device named Phantom Desktop

图15 交互式触觉绘制系统Fig.15 The interactive haptic decorating system

表2 虚拟画笔的主要参数Tab.2 Main parameters of virtual hairy brush
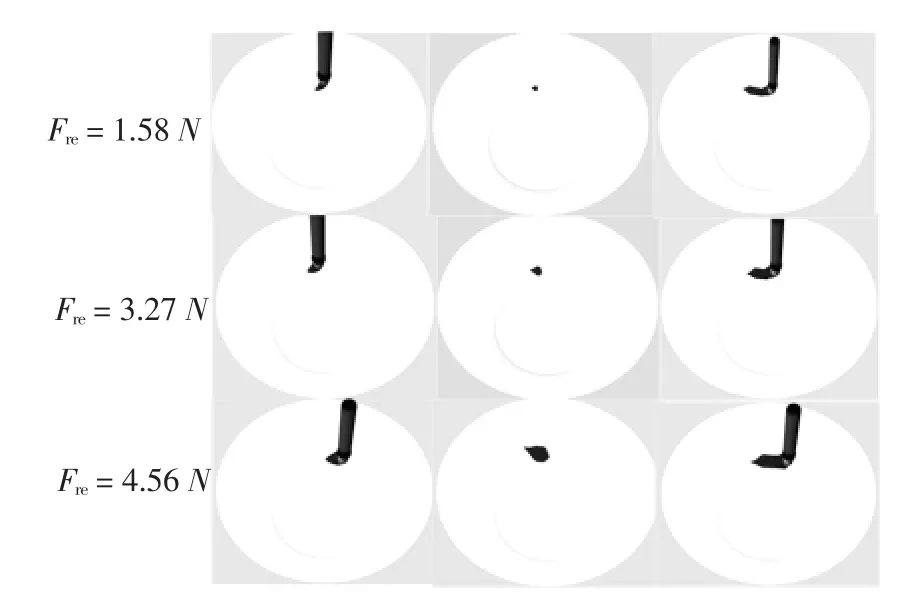
图16 当施加不同的压力时画笔笔头的变形Fig.16 Brush deformations are presented when exerting different types of pressure on the brush
作为一个简单的例子,中国汉字“七上八下”被绘制在一个碗模型的内表面(图17).
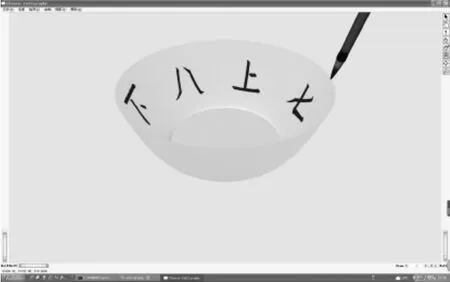
图17 中国汉字“七上八下”绘制在碗的内表面Fig.17 Character“七上八下”is drawn on the exterior of a bowl
图18 显示了使用交互式触觉绘制系统在3D 物体表面实施绘制的一个具体的实例(两只小鸭子被绘制在一个碗模型上).

图18 交互式触觉绘制系统中的一些具体的例子Fig.18 Some concrete examples of the haptic decorating system
在使用我们的画笔模型进行的另一组仿真实验中,画笔参数如表2 所示.中国汉字“漫步人生”被绘制在一个盘子模型的内表面(图19(a)).相比于采用“Moxi”二维绘制系统所得到的绘制结果(图19(b)),使用我们的系统可绘制出带有水墨扩散效果的三维笔道和字迹.在图20 中展示了仿真实验中得到画笔分叉效果.


图19 分别采用我们的系统以及“Moxi”系统创作的汉字“漫步人生”Fig.19 The Chinese character“漫步人生”created with our system and the“Moxi”system

图20 画笔笔头分叉效果Fig.20 Some bifurcation effects of the brush head are created
4 结论
基于实时力反馈交互技术,提出了一种新型的变刚度虚拟画笔模型及三维物体表面实时触觉装饰方法.针对虚拟三维表面绘制问题,深入研究了带有变刚度弹塑性的虚拟3D 画笔实时触觉行为.通过引入弯曲弹簧振子模型以构建3D 画笔力学模型,分析了画笔受力、姿态、含墨量与画笔变形之间的动态关系.类似于但又不同于数据驱动建模技术,我们建立了一种二维查询表,可以实现受力与相应笔头变形的快速求解.该画笔模型可以模拟实际画笔的许多重要特征,如:更软的画笔笔尖、画笔分叉等.实际上这些行为都是比较复杂的非线性物理现象,我们仅做了部分的有益探索.此外,为研究虚拟画笔与虚拟3D物体之间的碰撞检测问题,我们引入了一种基于“加权的平均距离”的碰撞检测算法.再采用一种有效的包围球扩展操作获得画笔的最小包围球,并计算得到虚拟投影平面.通过将虚拟投影平面上形成的2D 笔触实时的映射到3D 物体外表面就可以到画笔的3D 笔触.使用课题组开发的三维表面绘制系统,并运用Phantom Desktop 力反馈设备,较好的实现了三维产品外表面的触觉装饰,极大地增强了绘制过程的真实感,同时又能支持外观设计师创新灵感的发挥.
