考虑风电波动率的储能系统优化配置策略
2020-09-06陈泽西孙玉树张妍李美成
陈泽西,孙玉树,张妍,李美成
(1.华北电力大学 新能源学院,北京 102206;2.国网北京城区供电公司,北京 100034;3.中国科学院电工研究所,北京 100190;4.华北电力大学 经济与管理学院,北京 102206)
为了应对传统能源的短缺和环境污染等问题,可再生能源得到快速发展,并越来越受到人们的青睐.风力发电是可再生能源发电的重要组成部分,受天气条件的影响,风电具有波动性和间歇性等特点,其规模化并网会对电力系统的频率、电压和电能质量等安全可靠运行带来极大影响[1-3].储能系统能够灵活调节电力系统的功率输出,可应用于平抑风电的功率波动,提高风电并网的友好程度,促进电网对风电的规模消纳[4-5].
目前,国内外已经开展了关于平抑风电波动储能系统的优化配置的前期研究工作.一方面,设计了一种电池储能的缓冲策略以减少不稳定风电功率对电网的影响,并通过求解经济优化运行目标函数确定储能容量[6];也提出了基于磷酸铁锂电池的一种储能高效充放电控制方法,在配置最小容量的情况下实现对风电功率的滤波[7].另一方面,在平滑风电功率波动时,应用频谱分析方法来优化储能容量,使配置的储能容量最小[8].也可以应用多类型储能平抑风电功率波动,构建经济成本最小的储能配置与运行模型,应用智能算法进行模型求解[9].更有采用多类型储能吸收风电功率中不同频段的波动部分,将神经网络算法应用到储能配置的优化当中,建立经济性和功率平滑指标的耦合关系以实现多类型储能的高效运行[10].同时,为了提高并网风电的容量可信度,提出了基于改进的小波函数的混合储能优化配置策略,通过算例验证其有效性[11].
上述研究工作主要侧重于一种风电波动平抑下的储能配置问题,很少涉及到风电波动率对储能配置的影响.本文拟重点研究风电波动特性与储能配置之间的关系,挖掘波动率和储能功率、容量之间的内在联系,进而提出储能配置的评价指标,从而为风储系统的联合应用提供参考.
1 风电波动的平抑策略
对于可再生能源出力波动的平抑算法也有多种,包括一阶滤波[12]、经验模态分解[13]、小波包分解[14]、滑动平均[15]等,这些方法由于自身的特点,常常出现过度平抑情况.而模型预测控制(Model Predictive Control,MPC)策略由于具有提前预测、优先控制等特性,不会出现过度平抑情况,已被应用到风电功率波动平抑当中.通过对比模型预测控制与一阶滤波、经验模态分解、小波包分解算法,验证了模型预测控制算法在风电波动平抑中的优势[16].模型预测控制算法中状态空间模型和滚动时域策略是核心[17].
风电功率和储能系统的关系可表征为:
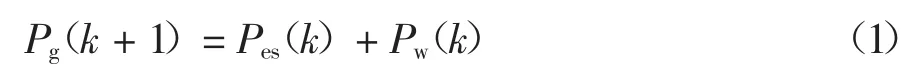
式中:Pg(k+1)为k+1 时刻平抑后的风电功率;Pes(k)为k 时刻的储能系统的功率;Pw(k)为k 时刻未平抑的风电功率.
储能的SOC(StateofCharge)可以由如下公式得到:
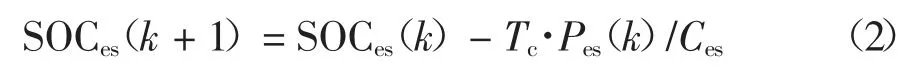
式中:Tc为系统的采样时间;Ces为储能容量.
状态空间模型中状态变量x1、x2分别定义为平抑后的风电功率Pg与储能SOCes;控制变量u 定义为储能功率Pes;扰动输入量r 定义为未平抑的风电功率Pw;输出变量y1、y2定义为Pg和SOCes(这是个迭代的过程,k 时刻的输出也是k+1 时刻的输入).
得到的状态空间方程如下:

利用滚动时域策略的思想,对式(3)进行迭代计算,可以预测未来k+M 时刻的输出变量,利用二次规划方法对每一个控制时域进行优化,获取相应的功率指令.
由此构建本文的系统模型,将每个优化周期的储能功率平方和最小作为优化目标,即:
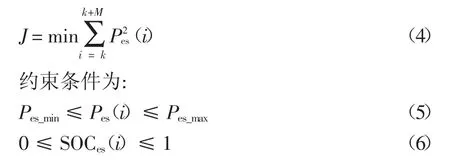

其中,式(5)为储能功率的最大值和最小值约束,式(6)为储能的SOC 约束,式(7)为并网波动率约束,即特定时间内最大功率与最小功率的差值,与额定装机容量Prated的比值.应用MPC 平抑风电波动的流程如图1 所示.
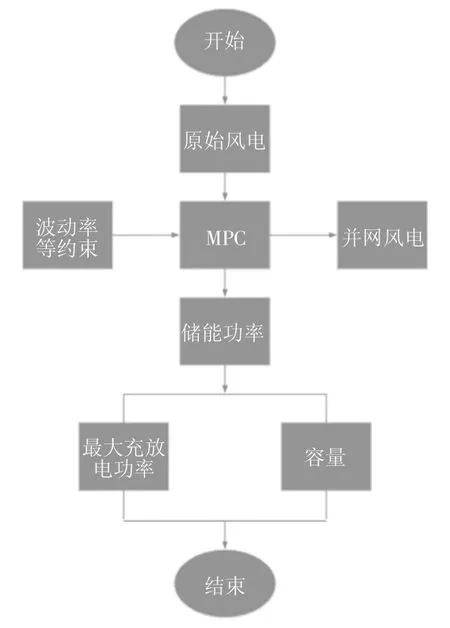
图1 MPC 控制流程图Fig.1 MPC control flow chart
2 从波动率角度分析不同风电的储能配置
以北方不同风电场为研究对象进行系统分析,各风电场具有相同的装机容量(100 MW)和采样率(5 s),并以1 min 波动率(2%)作为并网要求.
2.1 波动率与储能功率的关系
针对不同波动特性的风电场,本文主要从波动率角度出发,分析平抑风电波动所需配置的储能情况.1 min 风电波动率的计算公式为:
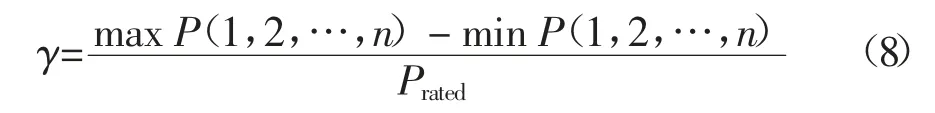
式中:max P(1,2,…,n)为该时间窗口的最大风电功率;min P(1,2,…,n)为该时间窗口的最小风电功率;Prated为风电装机容量.
将模型预测控制策略应用到图2 中的两组典型风电功率曲线,图3 为应用模型预测控制策略平抑前后的风电波动率.由图3 可知,平抑前WP1最大波动率为0.050 5,WP2最大波动率为0.066 5,即WP2的最大波动率大于WP1的最大波动率;平抑后两者的最大波动率均等于0.020 0(2%),即平抑后风电系统具有合格的并网波动率.
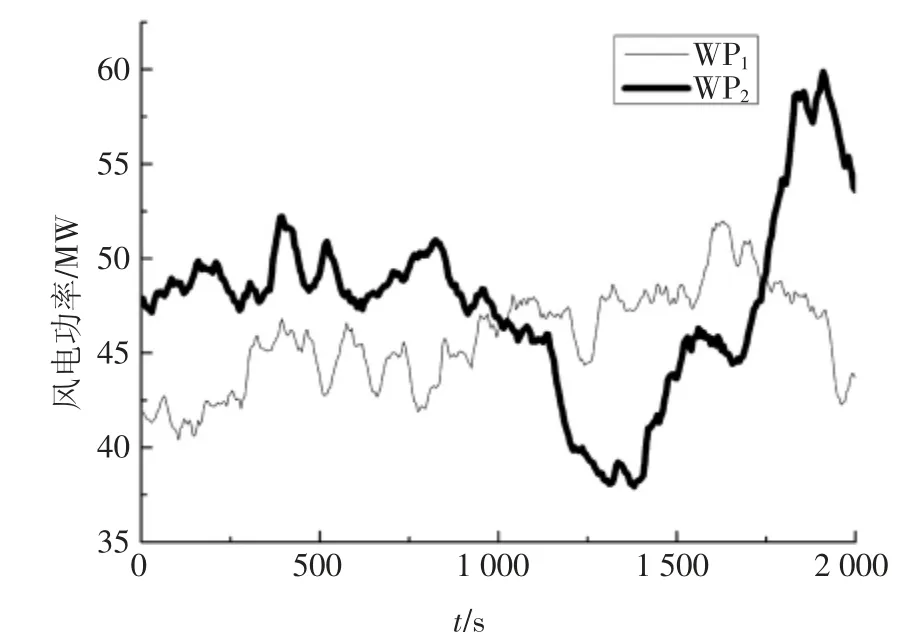
图2 两个风电场的功率曲线Fig.2 Wind power curves of two wind farms
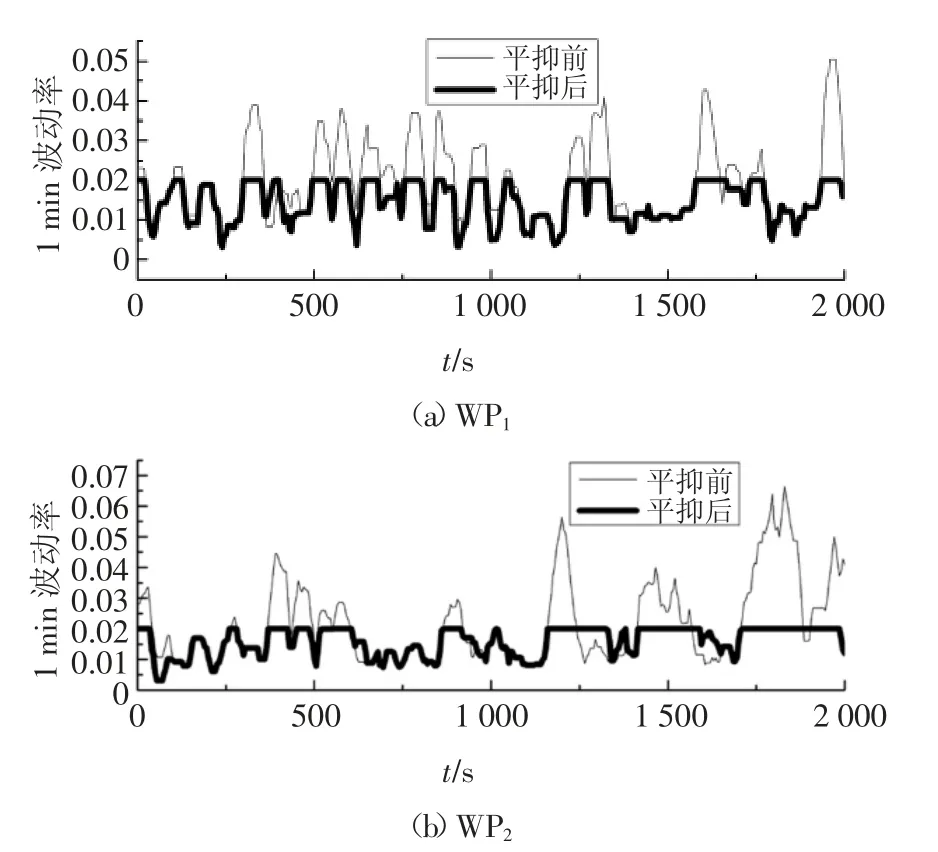
图3 平抑前后风电波动率Fig.3 Wind power fluctuation rate before and after smoothing
图4 为风电平抑所需的储能功率,可以利用式(9)计算出两组储能的最大充放电功率.

WP1最大充放电功率为3.049 6 MW,WP2最大充放电功率为8.259 3 MW,WP2最大充放电功率大于WP1最大充放电功率.
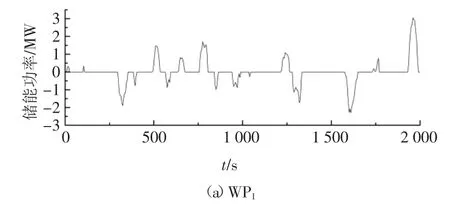
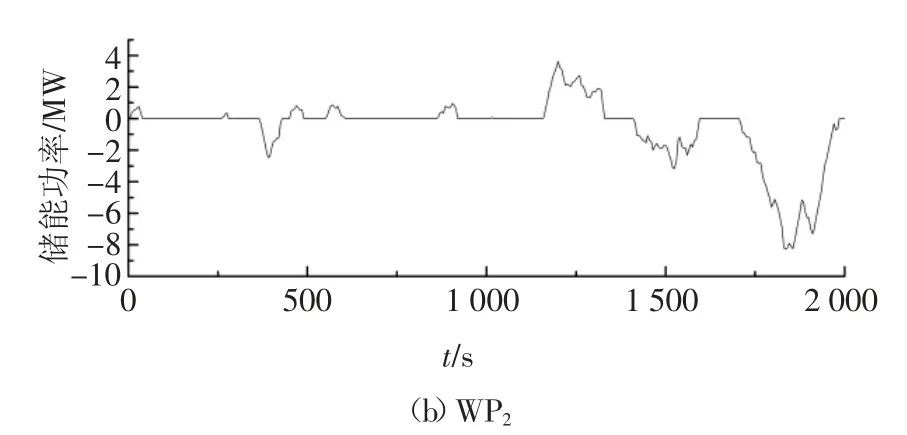
图4 用于平抑风电波动的储能输出功率Fig.4 Energy storage output power for smoothing wind power fluctuation
为了分析波动率与储能功率的对应关系,我们筛选出大于2%的波动率,并减去2%.为更加直观显示其对应关系,数值放大200 倍,将其和储能功率在同一个数量级进行对比,如图5 所示.另外,储能系统在平抑风电波动的过程中存在充电和放电两种状态,因此,其输出功率有正有负,本文取储能功率的绝对值,如图6 所示.由此可见,储能功率和波动率成强相关关系,当风电功率的波动率大于2%时(即图6 中波动率大于0 时),均需要储能充电或放电.此外,随着波动率增大,对应的储能功率也增大;反之,则减小.当波动率达到最大时,其对应的储能功率也最大.因此,WP2的最大波动率大于WP1,需配置的储能功率较大.

图5 实际储能功率与波动率的关系Fig.5 The relation between actual energy storage power and fluctuation rate
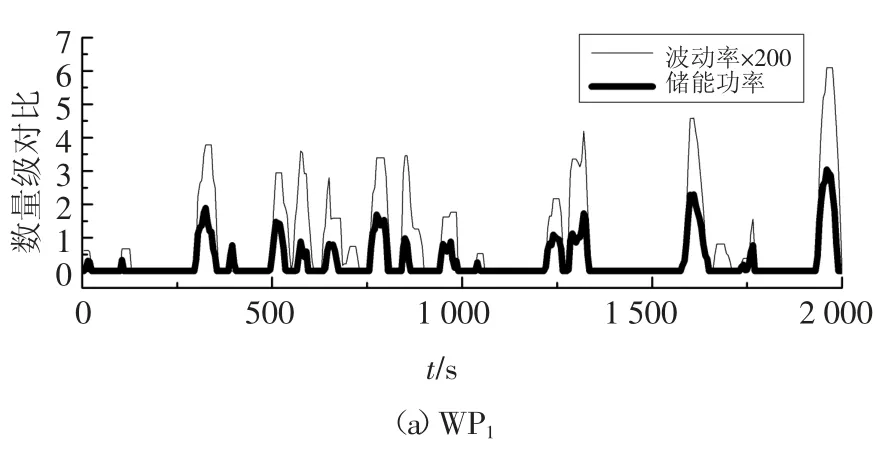

图6 储能功率绝对值与波动率的关系Fig.6 The relation between energy storage absolute value power and fluctuation rate
为了进一步验证上述结论的正确性,从波动率计算的角度进行分析,设定2%<γ1<γ2,得到以下推导过程:
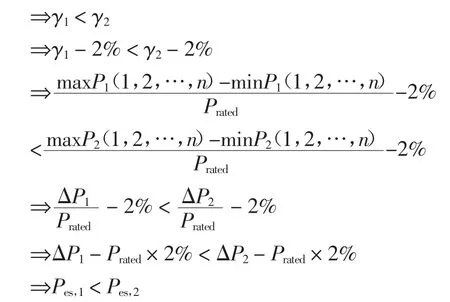
式中:ΔP 为该时间窗口内最大功率与最小功率的差值;Pes为需配置的储能功率.
由以上理论推导可见,风电的波动率越大,所需配置的储能功率越大.
2.2 波动率与储能容量的关系
基于风电波动率的概念,平抑风电波动所需的储能容量的计算公式为:

图7 为平抑WP1和WP2的风电波动储能能量变化曲线,根据式(10)计算出的WP1容量为0.041 2 MW·h,WP2容量为0.425 8 MW·h,WP1需要配置的储能容量小于WP2.
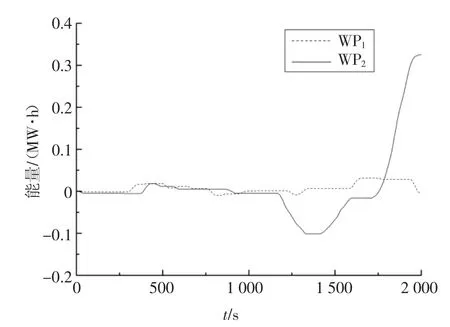
图7 储能能量曲线Fig.7 Energy curve of energy storage
为了更好地表征波动率对储能容量的影响,本文提出了正波动率和负波动率的概念.正波动率为在1 min 内,先出现功率最大值,后出现功率最小值,如式(11)所示:
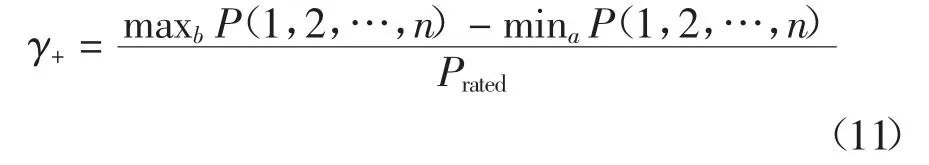
式中:maxbP(1,2,…,n)为1 min 时间窗口内先出现的最大风电功率;minaP(1,2,…,n)为1 min 时间窗口内后出现的最小风电功率.
负波动率为在1 min 内,先出现功率最小值,后出现功率最大值,如式(12)所示:
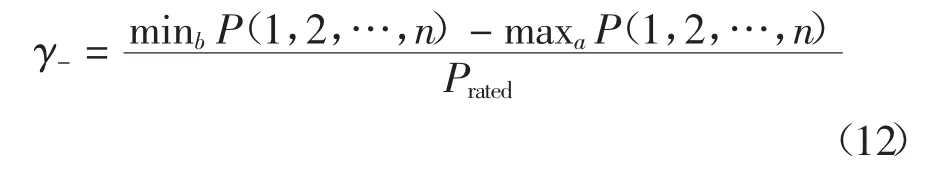
式中:minbP(1,2,…,n)为1 min 时间窗口内先出现的最小风电功率;maxaP(1,2,…,n)为1 min 时间窗口内后出现的最大风电功率.

图8 正负波动率示意图Fig.8 Schematic diagram of positive and negative fluctuation rate
图8 利用WP2的功率数据对正负波动率进行了说明,在360~420 s 内,先出现了功率最小值minbP,为48.330 7 MW;后出现功率最大值maxaP,为52.208 5 MW,其负波动率为-3.877 8%.在420~480 s 内,先出现了功率最大值maxbP,为51.560 8 MW;后出现了功率最小值minaP,为48.297 4 MW,其正波动率为3.263 4%.由此可见,当风电含有负波动率且绝对值大于2%时,功率平抑下储能需要吸收风电功率,即储能充电;反之,正波动率时,储能放电.
根据式(10)中的能量概念,本文提出了累计波动率(Cumulative Fluctuation,CF),即整个时间尺度内,将超出2%的正负波动率进行累计,可以得到累计波动率的变化曲线,如图9 所示.累计波动率的变化和储能能量的变化呈对应关系,即正波动率时,储能放电,功率为正;反之为负.
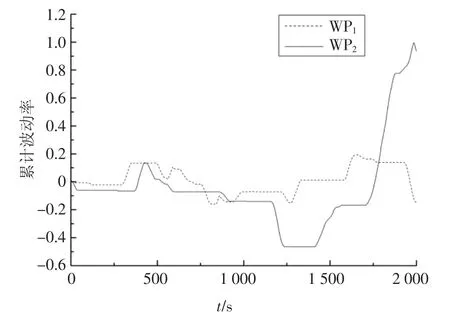
图9 累计波动率曲线Fig.9 Cumulative fluctuation rate curve
在累计波动率的基础上,提出应用累计波动率差值评估储能容量配置的方法.累计波动率差值(Cumulative Fluctuation Deviation,CFD)与储能容量的计算方式类似,具体如下:
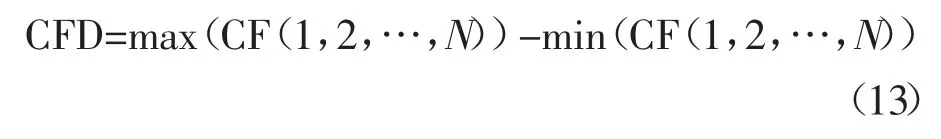
由式(13)计算出的WP1的累计波动率差值为0.357 6,WP2的波动率差值为1.462 6,WP1的累计波动率差值小于WP2,由此可得,在WP1累计波动率差值小于WP2时,其容量也小于WP2.
3 算例分析
为了进一步验证波动率和储能配置之间的关系,对以下3 类算例进行分析:1)一组风电的波动率在每一时刻都大于另一组风电的波动率;2)一组风电在某波动率范围内的功率点数均大于另一组风电在相同波动率范围内的功率点数;3)两组风电之间没有上述两种情况的关系,即随机选取的两组风电.
3.1 标准正弦风电系统
构建了如下两组同频率不同幅值标准正弦风电系统:
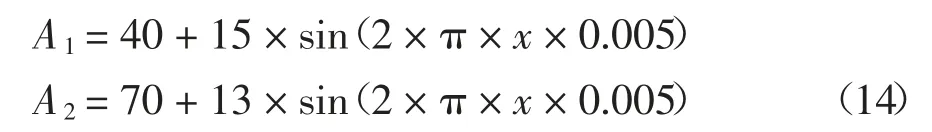
式中:A1、A2分别表示风电系统1 和2 的输出功率,单位为MW;x 表示时间,单位为s.
图10 为两个风电场风电功率波动平抑前后的示意图,可以看出,利用储能系统对A1和A2的风电功率进行平抑后,A1功率波动范围由30 MW 变为4 MW 了,A2由26 MW 变为了4 MW,两者波动均大幅度减小,且前者降低得更多.
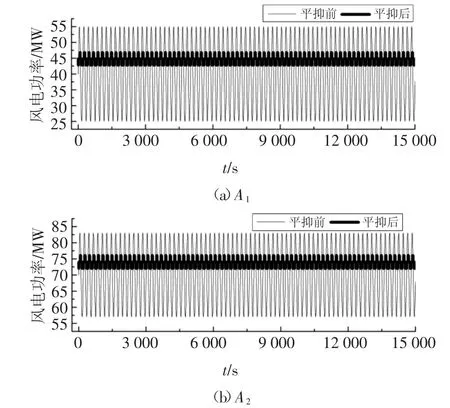
图10 平抑前后风电功率曲线Fig.10 Curves of wind power before and after smoothing
图11 中平抑前A1的波动率范围为0.061 8~0.242 7,A2的波动率范围为0.053 6~0.210 3,两者的波动率均在2%之上,A1的波动率之和为501.291,A2的波动率之和为434.449 5,且A1的最大波动率大于A2的最大波动率,经过平抑后两者的波动率都不超过2%.从图12 的储能功率曲线可以得出,A1配置的储能最大充放电功率为21.971 7 MW,A2配置的储能最大充放电功率为18.775 5 MW,A1配置的储能最大充放电功率大于A2.
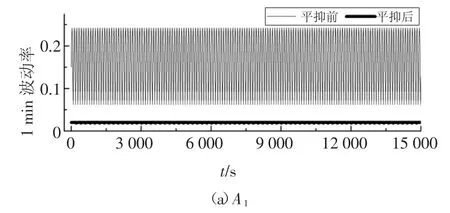

图11 平抑前后风电波动率曲线Fig.11 Curves of wind power fluctuation rate before and after smoothing

图12 储能功率曲线Fig.12 Curves of energy storage power
将A1和A2的原始波动率相减得到的差值均为正值,如图13 所示.由此可见,在每个时间点上,A1的波动率均大于A2.求得A1的容量为19.183 7 MW·h,A2的容量为15.818 5 MW·h,A1配置的储能容量大于A2.
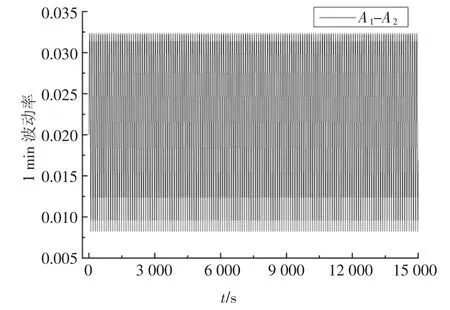
图13 波动率差值曲线Fig.13 Curves of fluctuation rate difference
针对同频率不同幅值的两组正弦风电,虽然A2的功率幅值大于A1,但是A1的最大波动率大于A2,A1配置的储能最大充放电功率大于A2,由此可得,配置的储能功率与风电的功率幅值无关,与功率幅值的变化值有关;此外,在所有时间点上,A1的波动率均大于A2,所以A1配置了较大的储能容量.
3.2 实际风电系统案例1
图14 为平抑前后的两组实际风电功率曲线,W1的功率波动范围值由16.157 0 MW 变为了15.990 5 MW,W2的功率波动范围值由27.849 9 MW 变为26.585 7 MW,前者降低了1.03%,后者降低了4.54%,两者的功率波动均减小,且W2减小得更多.

图14 平抑前后风电功率曲线Fig.14 Curves of wind power before and after smoothing
图15 中W1平抑前最大波动率为0.046 9,超出2%的功率点数为530 个,超出2%的波动率之和为3.025 2;W2平抑前最大波动率为0.061 6,超出2%的功率点数为705 个,超出2%的波动率之和为6.026 3,两者平抑后波动率均不大于2%.从图17 可以看出,W1的储能需配置2.689 6 MW 的最大充放电功率,W2的储能需配置4.1580 2 MW 的最大充放电功率.

图15 平抑前后波动率曲线Fig.15 Curves of fluctuation rate before and after smoothing
从图15 可以看出,在相同的时间点,W1与W2相比,其波动率有大有小,即在整个时间范围内,没有一个风电的波动率完全大于另一个.为此,分别统计了大于2%波动率的功率点数,如图16 所示.大于2%的以及每增加1%对应的功率点数,W2均大于W1.通过图17 中的储能功率曲线,计算求得W1的储能容量为0.142 3 MW·h,W2的储能容量为0.568 6 MW·h.
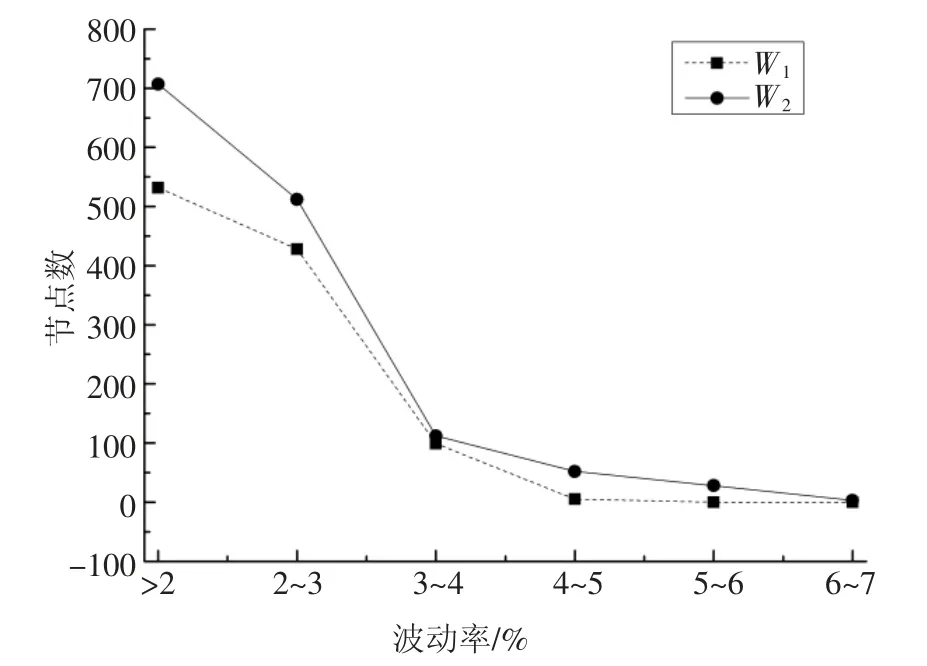
图16 波动率统计Fig.16 Fluctuation rate statistic
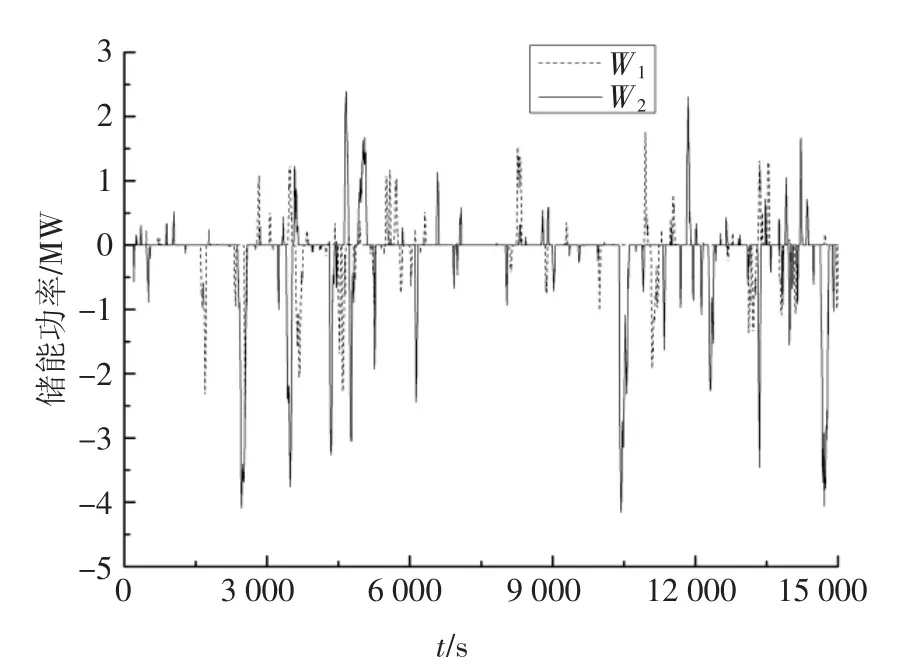
图17 储能功率曲线Fig.17 Curves of energy storage power
因此,W2的最大波动率较大,分析结果表明需配置的储能最大充放电功率较大;从统计的角度来看,由于风电W2在每个波动率时段含有的功率点数均大于W1,其所配置的储能容量较大.
3.3 实际风电系统案例2
从图18 和19 分析可得,本文所提的控制策略能够使风电具有友好的并网波动率.图18 中W3的功率波动范围值由34.140 1 MW 变为33.298 3 MW,降低2.47%,W4的功率波动范围值由39.024 1 MW变为36.889 2 MW,降低5.47%,后者波动降低较多.图19 中W3平抑前的波动率最大为0.080 6,波动率超过2%的功率点数为166 2 个,波动率之和19.242 2;W4平抑前的波动率最大为0.096 8,波动率超过2%的功率点数为151 4 个,波动率超过2%波动率之和为19.331 6.W4虽然波动率超过2%的功率点数较少,但是最大波动率和超过2%波动率之和均较大.W3和W4平抑后的波动率均不超过2%,通过图21可以求得W3的储能最大充放电功率为7.827 4 MW,W4的储能最大充放电功率为8.906 6 MW.

图18 平抑前后风电功率曲线Fig.18 Curves of wind power before and after smoothing

图19 平抑前后波动率曲线Fig.19 Curves of fluctuation rate before and after smoothing
从图19 中可以看出,W3比W4的波动率有大有小;图20 统计了不同波动率段的功率点数,W3比W4也是有大有小.
此时通过式(13)计算出W3的累计波动率差值为2.263 4,W4的累计波动率差值为3.478 8;通过图21 的储能功率曲线,计算出W3储能容量为0.803 5 MW·h,W4储能容量为1.031 1 MW·h.因此,波动率较大的风电需要配置较大的储能功率,累计波动率差值越大,需配置的储能容量也越大.
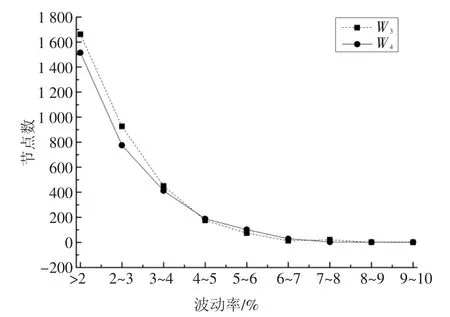
图20 波动率统计Fig.20 Fluctuation rate statistic
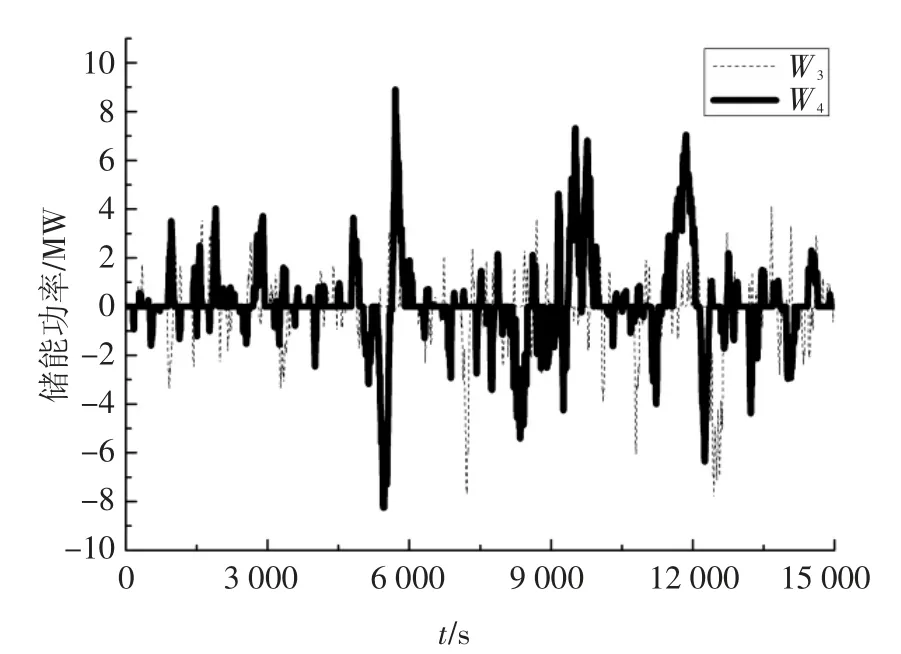
图21 储能功率曲线Fig.21 Curves of energy storage power
为了验证累计波动率差值的普适性,在相同时间尺度上统计算例中的6 组风电的累计波动率差值和容量,如表1 所示.
从表1 可以看出,不同的累计波动率差值,对应的储能容量不同;较大的累计波动率差值,配置的储能容量也较大.因此,应用累计波动率差值作为储能容量配置的评价指标具有合理性.
4 结论
本文提出了考虑风电波动率概念的储能系统优化配置方法,利用MPC 算法平抑风电的功率波动,并基于风电波动率对储能系统的优化配置进行分析,得出以下结论:
1)随着风电波动率的变化,配置的储能系统功率与其成正相关关系,波动率较大的风电场配置的储能功率也较大;针对不同波动特性的风电系统,最大波动率与储能最大充放电功率的配置也显示出正相关关系.
2)针对3 类不同波动率的典型实际场景进行分析表明,当A1的波动率均大于A2时,A1配置的储能容量大于A2;当W1各波动率段的功率点数大于W2时,W1配置的储能容量大于W2;而当W3和W4的波动率不能直接对比时,可应用累计波动率差值进行容量的对比分析.即在正负波动率的基础上,提出并应用累计波动率差值作为储能容量的评价指标,其数值越大的风电系统,需配置的储能容量也越大.
本研究所提出的累计风电波动率的概念可为储能系统的优化配置提供理论基础,对风电场的储能规划与运行控制具有一定的参考价值.另外,在今后的研究工作中,将进一步研究储能参与市场交易的策略以及可能的盈利模式,从而加快储能的产业化进程.
