基于策略迭代算法的连续时间线性Markov跳变系统非零和微分反馈Nash控制

2020-09-05朱国政张茂光何舒平

控制理论与应用 2020年8期

朱国政，张茂光，何舒平

(1.安徽大学电气工程与自动化学院，安徽合肥 230601;2.安徽大学计算智能与信号处理教育部重点实验室，安徽合肥 230601)

1 引言

Markov 跳变系统是1961 年由Krasovskii 和Lidskii[1]提出的一类多模态随机系统.在Markov跳变系统中，它包含模态和状态两个动态特性.作为一种多模态的系统，该系统可用来模拟具有突变特性的动态系统，如制造系统、网络控制系统以及容错控制系统等.在实际过程中，由于零部件失效、环境干扰以及子系统的连接方式改变等因素，Markov跳变系统也能用于模拟很多结构和参数具有突变效应的动态过程.

近几十年来，Markov跳变系统引起了学者们的研究兴趣并取得了很多研究成果.Sworder[2]研究了连续时间线性随机Markov跳变系统的二次型优化控制问题.之后，Blair等人[3]在连续时间Markov跳变系统的基础上提出了离散时间线性Markov跳变系统的最优控制方法.基于动态规划理论，Wonham[4]提出了另一个解决连续时间线性随机Markov跳变系统二次型优化控制问题的方法.Zhang等人[5]研究了一类具有部分未知转移概率的连续时间和离散时间线性Markov跳变系统的稳定性问题.Park等人[6-7]研究了离散时间Markov跳变系统的预测控制问题.当然还有很多其他关于Markov跳变系统的研究成果，如H2控制器设计[8-10]、H∞控制器设计[11-13]、鲁棒控制和滤波问题[14-16]、故障诊断问题[17-18]等.

在控制领域，优化控制问题一直是研究热点.要求解系统的优化控制器，最常用的解决方法是求解对应的Riccati方程.Kleinman等介绍了一种离线迭代算法求解Riccati方程[19].文献[20-21]给出了相关方法的收敛性证明.

随后，相关的Nash微分博弈的零和、非零和的优化控制问题也被应用到求解对应的Riccati 方程中[22-27].Nash 微分博弈是由文献[25]首次提出的.Nash 微分博弈通常出现在网络、无线通信[28]等较大的耦合系统研究中[29].当被控系统受到多个控制输入的影响时，就可以采用Nash博弈方法.当系统具有线性动态特性和无限时域二次成本函数指标时，Nash均衡的求解等价于求解一组耦合的代数Rittaci方程，如文献[22，25，30-31].文献[23，26，32-34]等采用了策略迭代的方法求解耦合代数Rittaci方程.这些算法可以得到收敛的代价函数系列.但是文献[26，32-34]中的收敛结果还没有确定.虽然在线性系统中关于Nash微分博弈的零和、非零和的优化控制问题取得了初步的研究成果，但是如何求解跳变系统的非零和微分反馈Nash控制问题，尚未取得较好的成果.

为了获得Markov 跳变系统的非零和微分反馈Nash控制策略，本文将相关问题转化为求解对应的耦合代数Riccati方程，并通过不断迭代耦合代数Riccati方程来计算可行解.本文提出的策略迭代算法过程包括:首先对跳变系统进行子系统的转换，在此基础上对模态之间的耦合关系解耦，并构成了新的策略迭代算法，最后通过数值仿真和对应的迭代更新结果证实算法的有效性和可行性.

2 系统描述

在概率空间(Ω，F，P)中，考虑如下一类连续时间Markov跳变线性系统:

该系统遵循以下概率分布:

式(1)－(2)中，Ω，F和P分别表示样本空间、事件场和定义在事件上的概率;x(t)∈ℝn是跳变系统的状态;x0是初始状态;u1(t)，u2(t)∈ℝm是系统的控制输入;A(r(t))，B1(r(t))，B2(r(t))是系统的系数矩阵;r(t)是一个连续时间和离散状态的Markov随机过程，它表示系统在某一时刻的模态，并在一个离散集中取值M={1，2，···，N};r0表示初始模态.本文假设式(1)是随机稳定的.

式(2)表示模态从时间t →t+Δt，系统从模态i跳到j的概率，其中i，j ∈M，Δt ＞0，，πij≥0(i/=j)，并满足.为了方便，令r(t)=i，那么A(r(t))，B1(r(t))，B2(r(t))3个系数矩阵可表示为Ai，Bi1，Bi2.

3 新的策略迭代算法

求解跳变系统(1)的非零和微分的反馈Nash策略前，先考虑如下一类连续时间线性系统:

给出如下的与控制量相关的二次成本函数:

其中Rij＞0，i，j ∈{1，2}和Qi均为实对称正定的权值矩阵.本文设定矩阵对，i ∈{1，2}是镇定可测的.

若每个控制器都要制定最佳策略，那么在非零和反馈控制策略下，可以使用具有闭环信息结构的Nash均衡，即一对反馈控制策略来获得.参考文献[35]，系统(3)对应的闭环系统的非零和反馈Nash均衡的最优控制策略可以通过以下方式得到:

上式两个控制输入的优化值，可通过正定矩阵Pi，i∈{1，2}获得.对于式(5)中的唯一正定对称矩阵Pi，i ∈{1，2}，可通过以下具有耦合关系的Riccati方程求解:

上式中的Sij，i，j ∈{1，2}，可表示为如下形式:

那么，对于线性系统(3)的两层非零和反馈Nash策略的相关问题可表述为耦合Riccati方程(6)的求解.为了求解相应的Riccati方程，给出如下引理.

引理1[26]满足耦合代数Riccati方程(6)的唯一正定实对称矩阵对(P1，P2)是一组稳定解，如果闭环矩阵(A－S11P1－S22P2)是Hurwitz的，即它的所有特征值均具有负实部.

为了获得新的算法求解耦合代数Riccati方程(6)的一对稳定解(P1，P2)，本文给出如下假设.

假设1为了保证求解的控制律是使得系统稳定的，本文假设是镇定可测的.

基于此，本文给出计算耦合Riccati方程(6)所采用新的策略迭代算法.通过算式变换将(6)改写为如下线性方程:

其中l表示迭代步数，且为大于0的整数.

本文所设计的用于计算耦合Riccati方程(6)的新的策略迭代算法具体步骤如下:

Step 1给出初始矩阵P01≥0，令l=1;

Step 2定义.在l ≥1下，通过迭代方程(8)求解正定解;

Step 3设定精确度阈值ε1和ε2.对于任意l ≥1，通过迭代算法(8)计算，直到满足;否则取l=l+1，继续执行Step 2;

Step 4获取非零和微分反馈Nash策略的正定解.

引理2[37]考虑如下代数Lyapunov方程:

其中:A为一般矩阵，Q ∈ℝn×n是正定对称矩阵，即Q=QT≥0.如果A是Hurwitz矩阵且Q ≥0，则方程(9)的唯一解X是正定矩阵.

引理3[26]如果是镇定可测的，那么由方程(6)得到的矩阵对(P1，P2)是唯一存在且正定的对称矩阵对.

如下定理(1)将给出在该算法中解得的矩阵序列(P1，P2)收敛的充分条件.

定理1对于耦合代数Riccati方程(6)，在任意l≥1时，存在如下正定矩阵:

那么由迭代方程(8)解得的迭代序列(P1，P2)是收敛的.

证由引理3可知，如果(A，B1)和(A，B2)都是稳定的，则通过耦合Riccati方程(6)求出的解(P1，P2)是正定对称的.考虑如下方程:

根据方程(10)，可对方程(11)做出如下变换:

在迭代步数为l+1时，方程(11)可表达为

将方程(12)减去方程(13)可得

以上是对于控制输入u1所对应的正定解P1收敛性的证明，同理也可以对控制输入u2所对应的正定解P2做出相应处理:

对于式(10)，由于S11≥0，在迭代中不断收敛所以只要满足初始条件≥0，那么在迭代过程中将会一直满足.

推论1如果引理1和定理1的条件满足，则由耦合方程(6)和(7)所定义的迭代序列(P1，P2)最终是收敛的.

注1 以上是将一类连续时间线性系统的非零和微分反馈Nash控制问题转化为求解相应的Riccati方程，给出了求解Riccati方程的策略迭代算法.但是该求解方法只适用于线性系统，不能直接应用于跳变系统.为了将该方法应用于跳变系统需要考虑到:首先要根据跳变系统的特性将系统进行子系统分解，然后对每个子系统进行解耦.进而，利用相应的迭代算法对跳变系统进行求解.接下去将对跳变系统的子系统分解和跳变解耦进行描述，并给出具体的算法步骤.

4 子系统分解和跳变解耦

对于Markov跳变系统(1)，给出如下的与控制量相关的二次成本函数:

其中Rij＞0(i，j ∈{1，2})和Qi均为实对称正定的权值矩阵.设定矩阵对，i ∈{1，2}是镇定可测的.

若每层都需要制定最佳策略，参考对线性系统的分析，系统(1)对应的闭环系统的非零和反馈Nash均衡的最优控制策略可以通过以下方式得到:

上式两个控制输入的优化值，可通过正定矩阵Pi，i ∈{1，2}获得.与线性系统最优控制策略(5)不同的是上式中R11，R22，P1，P2都和跳变的模态相关，它们之间存在着耦合关系.所以应用于线性系统的求解方法不能直接应用到跳变系统.

考虑到上述原因，本文对跳变系统进行子系统分解和跳变模态解耦[38].

定义1对于跳变系统(1)，在某一时刻t，可将其分解成多个子系统，那么第i个系统可写成如下的形式:

显然，式(18)中的各个子系统存在耦合关系.针对第i个模态，其对应的耦合代数Riccati方程可表示如下：

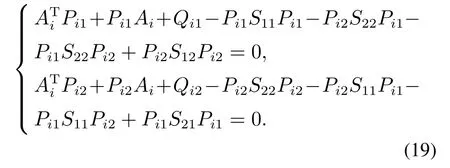
方程(19)可改写成如下形式:

其中i表示对应的模态，且在一个离散集中取值M={1，2，···，N}，并有.跳变系统的各个模态之间的解耦合关系可表述为

注2对于Markov跳变系统的每一个模态，需要获得对应的稳定解(Pi1，Pi2).在求解相应的Riccati方程时不仅存在同一模态下双控制器之间的耦合关系，也会存在跳变系统各模态间的耦合关系.对于这种双耦合关系，在处理过程中为了使得算法简单，本文假定每一模态下具有相同的Sij，其中i，j ∈M={1，2，···，N}.

在线性系统迭代算法的基础上，本文所设计的Markov跳变系统策略迭代算法和解耦过程的具体步骤如下:

Step 1给出初始矩阵对，令l=1;

Step 2定义.在任意l ≥1下，通过策略迭代方程(20)和策略更新方程(21)求解对应的正定解;

Step 3设定精确度阈值ε1和ε2.对于任意l ≥1，通过迭代算法(20)和(21)计算，直到满足;否则取l=l+1，继续执行Step 2;

Step 4获取Markov跳变系统非零和微分反馈Nash策略正定解.

定理2对于耦合代数Riccati方程(19)，在任意l ≥1时，如果存在如下正定矩阵:

由于定理2和定理1的证明相似，在此不再详细证明.

推论2如果引理1和定理2的条件满足，则由耦合方程(19)所定义的迭代序列(Pi1，Pi2)最终是收敛的.

对于Markov跳变系统的非零和微分反馈Nash策略的问题，新的策略迭代算法在对跳变系统子系统分解和解耦合后，将该问题转化为求解耦合代数Riccati方程(19).在跳变系统的每一个模态都能得到一对稳定解(Pi1，Pi2)，即可以通过求解N个并行的方程(19)实现对该系统的优化控制.

在文献[35]所提出的算法中，代数Riccati方程的解依赖于系统的系数矩阵和终值，所以无法保证算法的收敛性.文献[36]所提出的算法中，给出了求解代数Riccati方程的方法，却没有给出保证迭代解收敛的充分条件.本文所提出的算法中，给出了算法解得的矩阵序列的充分条件，并且将其应用于Markov跳变系统.

接下来将给出相应的数值仿真示例来验证本文所设计算法的正确性和迭代收敛的效果.

5 算法仿真实例

5.1 实验1

本文将通过给出如下示例来验证上述算法的有效性和收敛性.在求解之前先给出初始数据.

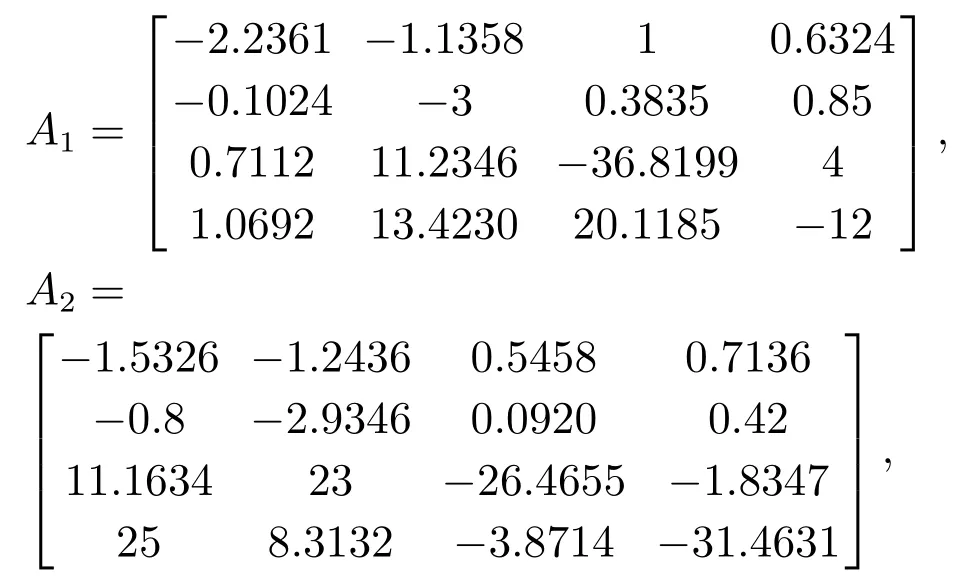
对于跳变系统(1)所对应的耦合Riccati方程(19)，给出模态数N=2的如下四维系数矩阵:

为了求解方便，令

选取跳变系统的转移矩阵如下:

那么子系统分解后的系数矩阵可通过如下公式获得:

两个模态下的Rij的值如下:

其他相关的数据可以通过方程(18)解得.

对于双控制器输入模型，第1个模态下的稳定解为

应用同样的迭代算法，计算出第2个模态下的稳定解为

在以下的仿真图中，图1－4分别绘制出了Markov跳变系统非零和微分的反馈Nash策略问题的求解更新过程.图1绘制了模态i=1时求解的正定解Pi1的更新过程，图中的“*”体现出Pi1迭代更新的过程;通过模值的范数可以看出Pi1最终是收敛的，且在迭代步数l=9时收敛到精确值.图2绘制了模态i=1时求解的正定解Pi2的更新过程，从图中可看出在迭代步数l=8时Pi2收敛到精确值.图3绘制了模态i=2时求解的正定解Pi1的更新过程，从图中可看出在迭代步数l=9时Pi1收敛到精确值.图4绘制了模态i=2时求解的正定解Pi2的更新过程，从图中可看出在迭代步数l=8时Pi2收敛到精确值.该仿真示例更进一步体现了算法的正确性和可行性.

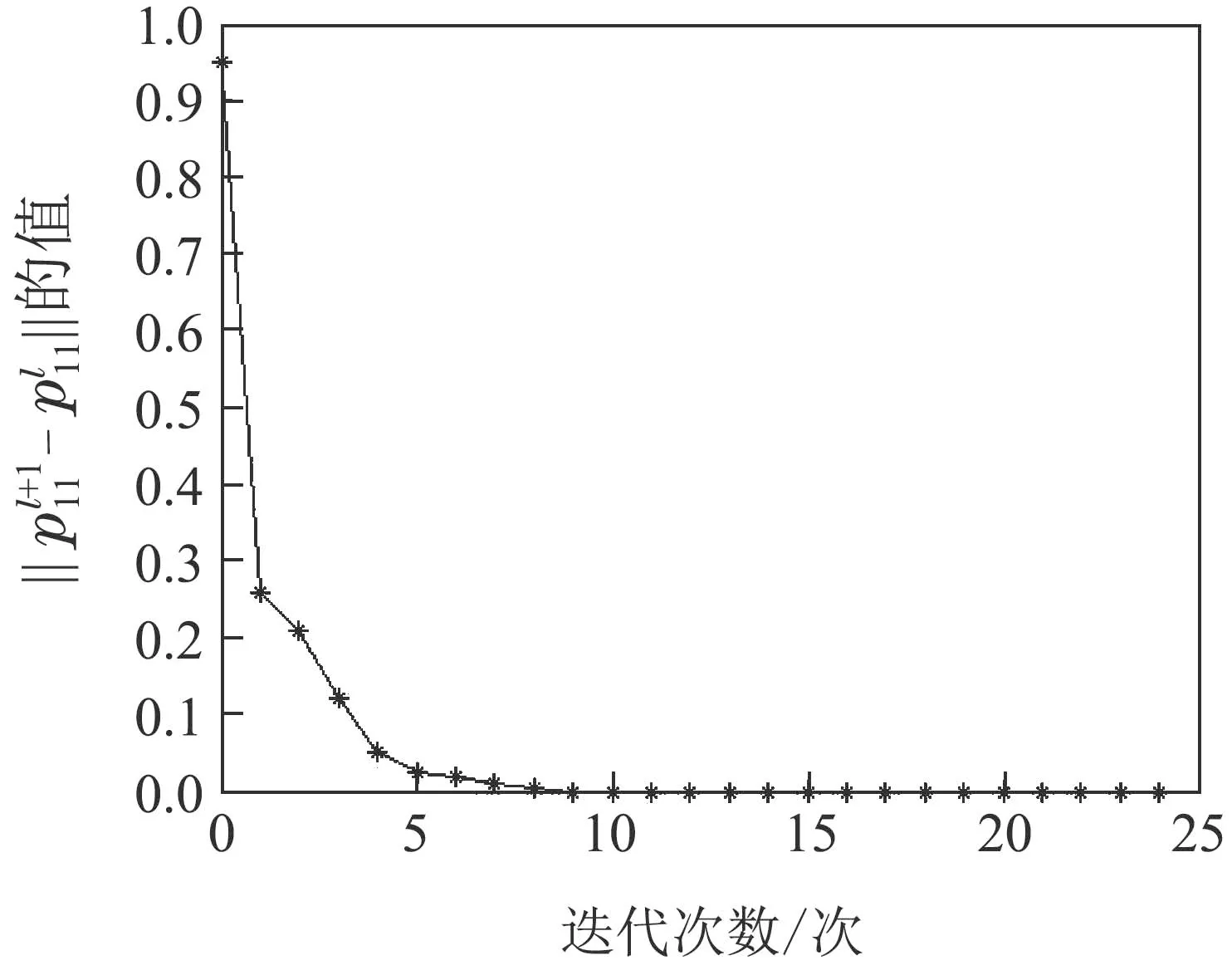
图1 运行轨迹图Fig.1 Thetrajectory diagramof

图2 运行轨迹图Fig.2 The trajectory diagram of

图3 运行轨迹图Fig.3 The trajectory diagram of

图4 运行轨迹图Fig.4 The trajectory diagram of

5.2 实验2

为了验证本文中所提出的算法对于非零和耦合代数Riccati方程的优越性，笔者将其和文献[35-36]中算法1(Algorithm 1，A.1)及算法2(Algorithm 2，A.2)的两种数值算法进行了对比，并做了如下实验:

对于耦合代数Riccati方程(5)和(6)，给出如下矩阵:

图5和图6分别绘制了3种算法对于求解非零和耦合代数Riccati方程的解P1和P2的更新过程.其中:菱形线表示本文中所设计算法的求解更新过程，实线代表文献[36]中算法2的求解更新过程，点线代表文献[35]中算法1的求解更新过程.从图中可以看出本文所设计的算法在求解非零和耦合代数Riccati方程时可以更快地得到稳定解.图5表示在求解P1时，本文的算法需要3次迭代就可以求得稳定解，而A.2和A.1分别需要7次和8次迭代才能求得稳定解.图6表示在求解P2时，本文的算法需要2次迭代就可以求得稳定解，而A.2和A.1分别需要4次和6次迭代才能求得稳定解.此外，文献[35-36]中没有对两种算法的收敛性进行证明，而本文给出了对所设计算法中解得的矩阵序列(P1，P2)收敛的充分条件，并且给出了证明.从以上分析可以看出本文的算法更有优越性.