基于模糊决策的随机森林算法

史金余，杨泽宇，谢 兄

(大连海事大学 信息科学技术学院，辽宁 大连 116026)

0 引 言

随机森林[1]组合了Bagging和随机子空间两种技术，为了获得更好的组合正确性，需要保证单棵决策树的正确性和多样性[2]。许多学者对随机森林算法进行了广泛的研究，刘晙提出一种基于多模糊核约束的随机森林算法，主要解决了超分辨率图像的鲁棒性问题[3]。吴辰文等利用变量预测和选择的方法来提高随机森林的预测精度[4]。Abellán等利用不精确概率和一般不确定度量的标准，改进随机森林的基分类器，提出基于不精确概率理论的随机森林算法(CRF)[5]。Xia等通过属性强度来调整投票权重，提出一种加权投票随机森林算法，能够成功地处理不完整数据的分类任务[6]。现有的随机森林算法没有考虑属性重要度与结点分裂的关联性，忽略了重要度低的属性对分类结果的影响，导致随机森林在处理分类问题时的正确率受到限制。传统的随机森林算法选择属性是完全随机的，这就说明每一个属性被选择的概率是相等的[7]。事实上，属性重要度低的属性应该对最后的分类结果影响小。为了更好地解决这一问题，本文研究了一种基于模糊决策的随机森林算法，利用属性重要度生成决策树，舍弃部分重要度较低的属性，从而减小了重要度低的属性对最后分类结果的负面影响。同时利用叶子结点被赋予的权重和类别分布情况得到决策树的判定结果。最后在UCI数据集上验证算法的有效性。

1 随机森林相关理论

1.1 属性重要度

众所周知，决策树中的属性为条件属性，属性的重要性对最终的决策结果有一定的影响[8]。属性重要度概念是指所有条件属性集中，属性对信息增益贡献的重要性对比结果。

传统的信息增益公式中，分支结点中包含的样本数越多，则给分支结点赋予的权重越大[9]。针对此种情况，本文定义属性重要度的计算公式如下

(1)

其中，训练集D={(x1,y1),…,(xi,yi),…,(xm,ym)}，xi为一个样本，yi为xi所对应的类别，总类别数为m。Dv为属性a的V个可能取值{a1,a2,…,aV}中，第v个分支结点包含在D中的取值为av的样本。|D|为训练集D中数据的个数，|Dv|为数据集Dv中数据的个数。L(a)为属性a具有的不同属性值的个数。而Ent(D)为信息熵，文献[10]已给出信息熵的定义[10]。

1.2 随机森林算法

随机森林是一种以决策树为基学习器的集成学习算法，它的特点之一就是在决策树的训练过程中利用了随机属性选择[11]。文献[12]表明随机森林的分类错误率与任意两棵决策树的相关性和每棵决策树的分类能力是密切关联的[12]。文献[12]也指出到目前为止，关于两者关系对随机森林性能影响的研究很少。

随机森林中每棵决策树的生成过程都有两个特点：随机且有放回地从训练集中选择训练样本作为训练集和随机地从属性特征中选择特征子集，并且生成的每棵决策树都完全生长，没有剪枝过程。

决策树通过将数据集划分为更小和更同质的子集，以分而治之的方式工作。属性的选择是完全随机的，这就说明每一个属性被选择的概率是相等的。事实上，数据集的递归划分意味着较低级别的子集具有非常少的实例。在某些数据集中，特定节点上的实例可以低至2-5个实例[13]，用这么少的无关紧要的数据做出可靠的决定是不可能的。

2 基于模糊决策的随机森林算法

2.1 基本思路

随机森林中每一个属性的重要程度不同，对结点的分裂影响也不同。为了减小属性重要度低的属性对分类结果产生的消极影响，避免传统的随机森林算法中偏向选择属性取值多的属性作为分裂结点，本文利用属性重要度的概念，把属性重要度作为选择最优划分属性的准则，但每棵决策树无论重要度大小，在投票时权重都相等，某些节点上的实例存在数量极低的情况，即属性重要度极小的属性。属性重要度小的结点存在无法继续分裂下去的情况，这样就会造成此结点分裂不纯，在这种情况下会选取数量最多的类别作为当前叶结点的分类结果，而这与实际情况往往不符，影响随机森林的分类正确率。

为了降低上述情况构建出的决策树对整个模型的影响，本文结合属性重要性的计算方式，对属性重要度值排序，设置属性重要度的阈值，舍去部分重要度较低的属性，把明确决策树(即完全生长的决策树)转化为模糊决策树。由此去掉了无法继续分裂的不纯叶结点，减小了重要度低的属性对最后分类结果的干扰，使其父结点变为叶子结点，得到一棵新的决策树。在新的决策树中，对叶子结点中的各个类别赋予相应的权重，根据权重和此叶子结点上的类别分布情况，计算得到能够判定样本类别的模糊概率。由此递归地构造多棵决策树，根据这些决策树的投票结果，得到最后的分类结果，进行随机森林算法的优化，提高分类正确率。

2.2 具体步骤

基于模糊决策的随机森林优化算法的核心分为两部分，类别分布矩阵和模糊概率。

(1)类别分布矩阵

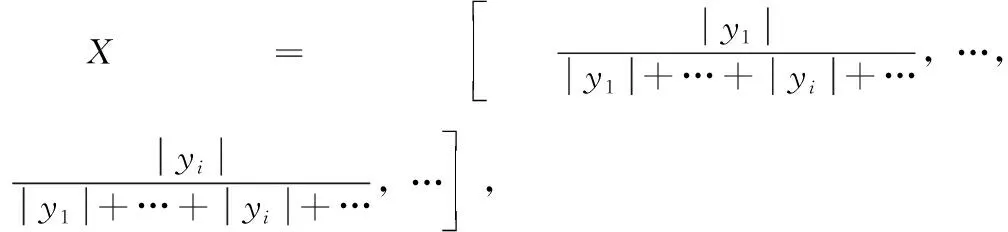
(2)模糊概率p(x)

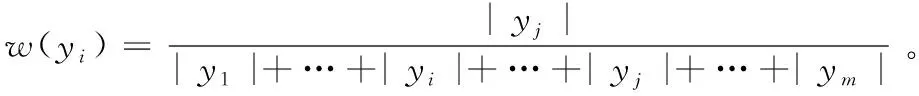
p(x)=w(yi)·X

(2)

最大模糊概率P(x)为

P(x)=argmax{p(x)}

(3)

(3)算法的具体步骤

输入：

训练集D={(x1,y1),…,(xi,yi),…,(xm,ym)}，迭代次数为B

输出：优化后的随机森林分类器F′(x)

步骤1 利用bootstrap方法从训练集中重采样随机选出n个样本；

步骤2 在所有样本上，通过调用以下步骤递归地构造模糊决策树。当达到预设阈值或叶子结点内只包含同一类别时停止生长，生成模糊决策树Tb(1≤b≤B)：

(1)从所有属性中随机选择出p个属性；

(2)根据属性重要度式(1)计算出属性重要度值，从而在p个属性中选择具有最大属性重要度值的属性作为最佳属性/分裂点；

(3)根据最佳属性/分裂点，将结点拆分成子结点；

(4)计算所有属性重要度值的均值，将其设为阈值，对比属性重要度的值与阈值的大小，去掉属性重要度低的结点，得到模糊决策树；

(5)计算模糊决策树中叶子结点的类别分布矩阵X；

(6)计算类别占比，得到权重w(yi)(1≤i≤m)，根据式(2)，计算出模糊概率p(x)；

(7)根据式(3)得到最大模糊概率P(x)，进行此棵模糊决策树的类别判定。

(4)

其中，Fb(x)为第b个决策树的类预测，majorityvote为投票结果的最大值。

(4)算法代码描述

Input: 训练集D={(x1,y1),…,(xm,ym)}，决策树棵树B

Output: FRF分类器F′(x)

步骤1 计算属性重要度gain*。

def gain*(D):

return gain_node;

步骤2 决策树Fb(x)。

def decision_tree(D)：

if len(set (classList)) == 1:

return classList[0];

bestFeat = gain*(D);

threshold = average(bestFeat);

if bestFeat < threshold：

del(sub_names[ bestFeat ]);

length = len(y);

class_1 = y.tolist().count(class_type[ 0 ]);

class_2 = y.tolist().count(class_type[ 1 ]);

class_1_ratio = class_1/length；

class_2_ratio = class_2/length；

class_1_proba =

class_2_ratio*y_pred_proba[：， 0 ];

class_2_proba =

class_1_ratio*y_pred_proba[：， 1 ];

result=np.column_stack((

class_1_proba,class_2_proba));

Fb(x)= { result:{}};

return Fb(x);

步骤3 FRF分类器。

def random_forest(count)：

for i in range(count)：

decision_tree(x,y,X_test);

return F’(x);

从以上伪代码中可以看出时间复杂度为o(n)，算法的改进并没有增加传统随机森林算法的时间复杂度。

2.3 实例分析

在对随机森林算法进行优化后，以“影响去打网球的因素”为例对其进行分析，对优化后的算法过程做进一步的阐述。其中，采用表1数据集：气象数据集，都是标称属性(outlook、temperature、humidity、windy、play)[14]。

表1 气象数据集

下面利用属性重要度作为最佳属性/分裂点构建决策树，对优化后的随机森林算法步骤进行简析：

(1)根据式(1)计算属性重要度，对属性重要度的值进行排序，找到最佳属性/分裂点，每次选择分裂结点的属性重要度值gain*见表2，递归地执行此步骤，直到叶结点不能继续分裂，进而构建一棵完全生长的决策树；

表2 最佳分裂属性选择gain*值

(2)设置属性重要度阈值，此例中为-0.5，根据阈值，去掉重要度小于此值的结点，得到一棵模糊决策树，如图1所示，为了便于叙述，设置编号结点Node，其中samples代表样本数量，value代表分类结果；

图1 模糊决策树

(6)将每棵模糊决策树的对应类别的模糊概率相加，根据式(3)得到最大模糊概率；

(7)最后由式(4)得到最后决策结果。

图1是通过属性重要度得到的结果，图1的overlook属性更远离根结点，从而弥补了原始算法偏向选择属性值较多的属性的不足，并且根据设置的属性重要度的阈值，降低了属性重要度低的属性对分类结果的影响。

3 实验验证及分析

3.1 实验描述

本文实验硬件平台采用Intel(R) Core(TM) i5-6200U型号CPU和8 GB内存的PC机；代码执行平台为Windows 10，Python 3.6，算法实现采用Python语言。在本次实验中，设置决策树的棵数的参数值为100，属性重要度的阈值为计算出的属性重要度的均值。

为了方便比较和分析，在UCI数据集中选取了6个不同数量、不同属性个数的二分类数据集，表3中列出了这些数据集的分布情况。

表3 取自UCI的实验数据汇总

为了说明FRF算法的改进效果，本文实验分别验证传统的RF算法，文献[5]提出的CRF算法与本文提出的FRF算法。

3.2 实验结果及分析

在每个数据集上，为了增加实验结果的可信度，采用交叉验证的方法，将数据平均分成9份，每次用其中8份做训练，1份做测试，循环8次，统计平均正确率，结果见表4，表5和表6。

表4 传统RF算法正确率结果

3组实验下的平均正确率折线图比较如图2所示。

从图2中可以看出，通过类别分布得到权重，再根据普通决策树的属性重要度设置阈值，去掉了重要度低的属性，从而将决策树的单一决策结果转化为多类分布结果。进而改善了分裂不纯的叶节只选择数量多的类别作为分类结果的情况，修正决策树误判的结果，消除了属性重要度较低的属性对决策树分类造成的负面影响，使改进后的随机森林算法的测试结果正确率高于传统的随机森林产生的测试结果。

表5 CRF算法正确率结果

表6 FRF算法正确率结果

图2 实验平均正确率对比

为了验证FRF算法的有效性，计算出测试集数据的查准率、查全率，公式如下。其中，TP为真正例，FP为假正例，TN为真反例，FN为假反例。

查准率

(5)

查全率

(6)

利用式(5)和式(6)计算查准率和查全率的数据见表7。

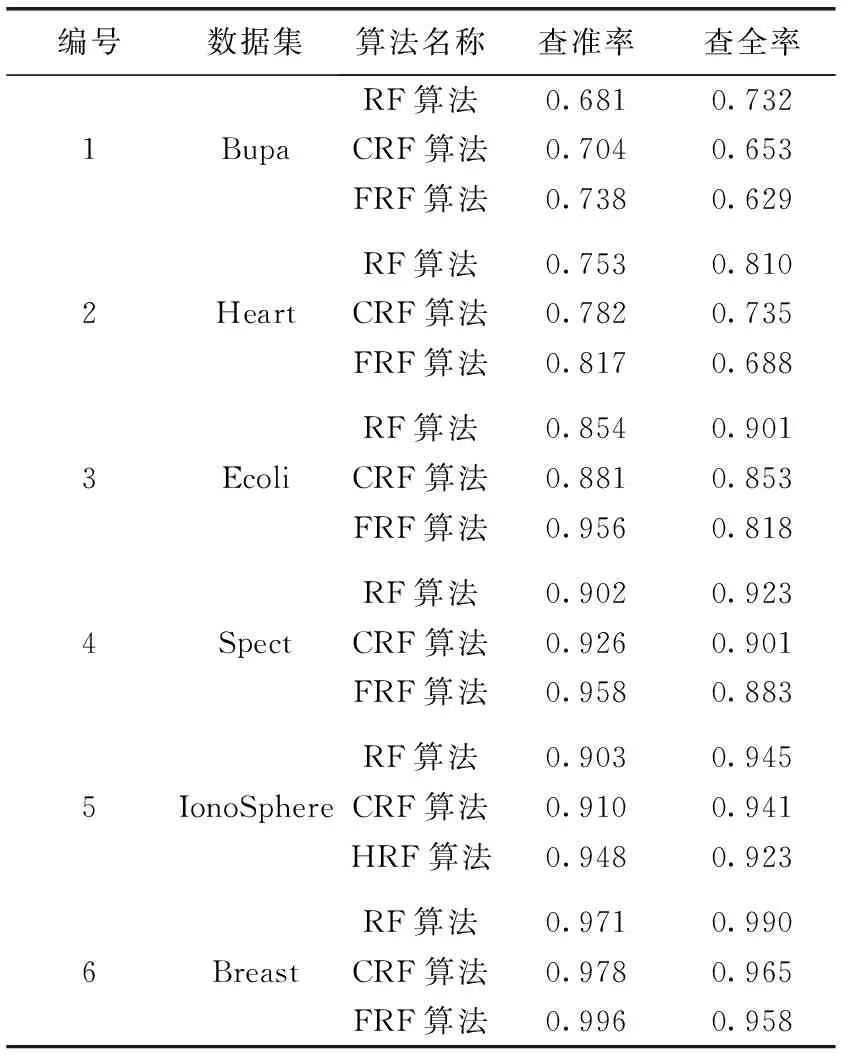
表7 查准率和查全率结果

以查准率为纵轴、查全率为横轴，得到的“P-R曲线”，如图3所示。“P-R曲线”图的定义请参见文献[10]。

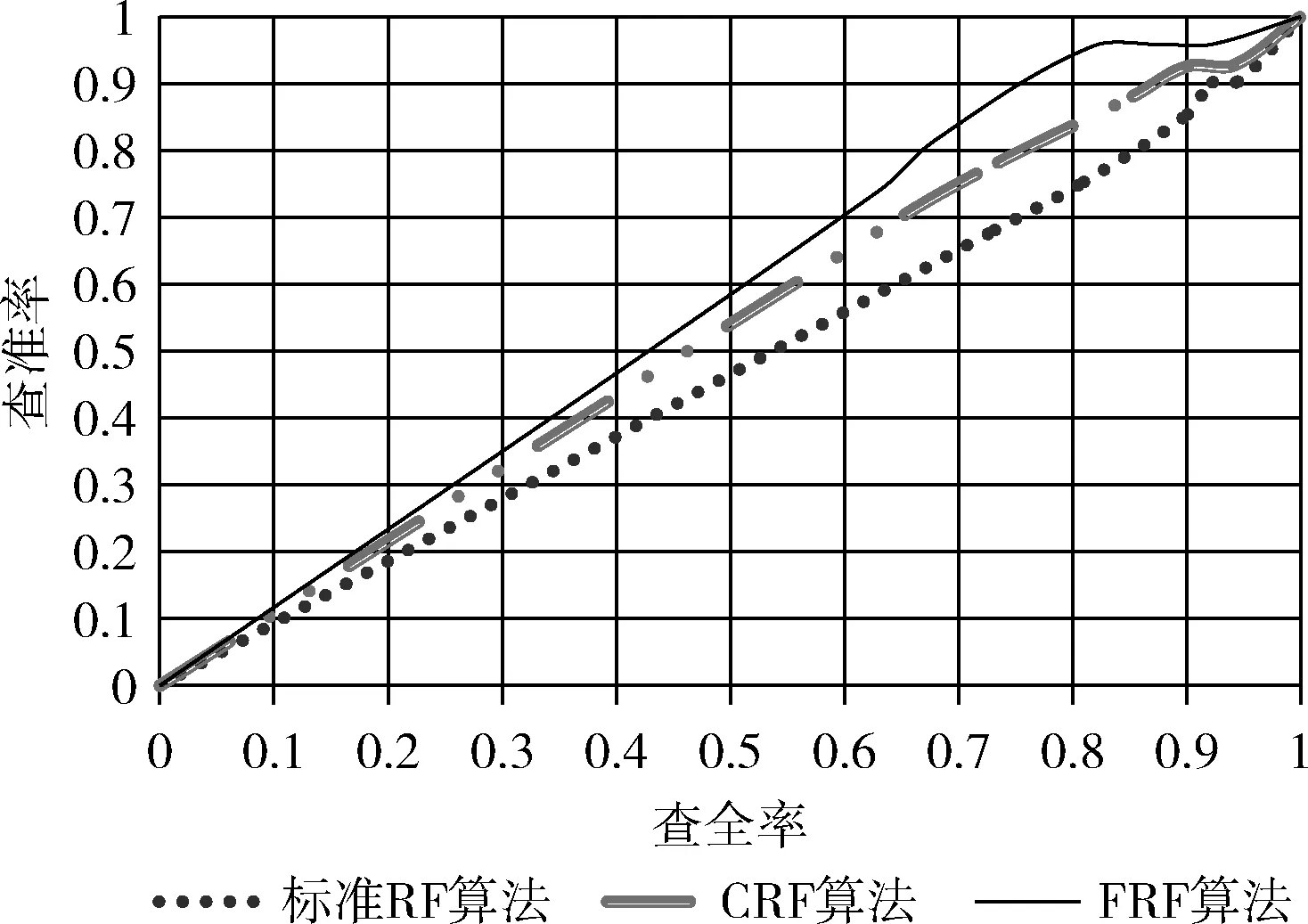
图3 P-R曲线

由P-R图可直观地看出各算法在总体样本上的查准率、查全率。文献[10]指出进行比较的学习器，性能优的学习器的P-R曲线会“包住”另一个学习器的曲线[10]。由图3可以看出本文提出的FRF算法总体上有了一定的性能提升。对于查全率而言，性能指标有了一定的下降，但这是一个正常的情况。在一个分类器中，想要更高的查准率，那么阈值要设置的更高，只有这样才能有较高的把握确定预测的正例是真正例。一旦把阈值设置高了，则预测出正例的样本数就少了，那真正例数就更少了，查不全所有的正样例，这就导致了查准率较高的情况下，查全率会较低一些。

根据以上图表数据可以得到，优化后的随机森林算法相比较于文献[5]中提出的CRF算法和传统的随机森林算法在Breast、Ecoli、Bupa、Heart、IonoSphere及Spect这6个数据集上均取得了最优分类正确率，充分展示了FRF算法对高维数据集的分类能力。实验结果表明，本文提出的基于模糊决策的随机森林算法较好提高了随机森林分类正确率，在性能评价指标查准率和查全率的结果分析图中也得出了优化后的随机森林算法性能有了一定的提高。

4 结束语

为了使随机森林算法具有更高的分类正确率，降低重要度低的属性对整个模型的影响，本文在属性重要度构建决策树的基础上，对属性重要度设置了阈值，由此得到一棵模糊决策树。又根据类别占比得到的权重，修正决策树误判的结果，降低了重要度低的属性对决策树分类结果的影响，提高了传统随机森林算法的分类正确率。本文提出的优化算法较好适用于样本数据分布不均匀的分类问题，该算法在实验中取得了较好的结果。虽然优化后的随机森林算法在正确率上有了一定的提升，但在研究中我们也发现属性重要度阈值对随机森林性能的优化有一定的影响，在今后的工作中，我们会对上述参数继续进行研究，以达到更好的优化效果。