无线传感器网络节点的三维定位技术
2020-09-04高瑞娟陈桂芬
高瑞娟,陈桂芬,徐 赫
(长春理工大学 电子信息工程学院,吉林 长春 130022)
0 引 言
传感器节点包括静止节点和移动节点,这些节点通过自组织的方式构成无线传感器网络(wireless sensor networks,WSN)[1,2]。基于无线传感器的研究主要有节点定位技术、网络覆盖技术和路由协议技术等方面,本文将对众多技术中的定位技术进行研究。
随着当今时代技术的发展,许多传感器技术被应用于大型农业中,例如无线温度传感器、无线光照传感器等。然而在规模较大、环境恶劣、地形较复杂的农田中部署的传感器一般是通过飞机随机抛洒的,这就意味着对随机抛洒的传感器节点进行准确定位成为获取农田可靠温度、光照、气体等信息的前提。目前,有许多学者对DV-Hop定位算法进行了改进[3-5],但这些仅适用于二维空间。由于实际环境的复杂性,二维空间的定位算法已经满足不了定位精度的需求,需上升到三维空间进行研究。
目前为止,三维空间中的定位算法有Landscape-3D(landscape three-dimensional)算法[6]、APIS(approximate point in sphere)算法[7]、3D-DV-Hop (three-dimensional distance vector-hop)算法[8]、Constrained-3D(constrained three-dimensional)算法[9]等。其中,众多算法中的3D-DV-Hop定位算法计算相对简单,所以有许多学者将其进行改进[10,11]。但这些改进算法并没有考虑锚节点共面问题,因此本文将对节点定位中存在的共面问题进行深刻研究,提出一种适用于三维空间中的锚节点组按规定路径移动的非测距定位算法。
1 3D-DV-Hop定位算法介绍
三维空间中DV-Hop定位原理类似于二维空间中DV-Hop定位原理,具体介绍如下:
(1)获取最小跳数
大量节点在监测区域内被随机部署后,锚节点通过向周围节点发送自身包含ID号、位置信息以及跳数hi的数据包信息[12]。其中,跳数hi开始值记为0。未知节点不断接收来自周围锚节点的数据包,若接收到的数据包中的跳数小于已经保存的最小跳数,则抛弃已经保存的跳数,同时把当前跳数进行加一,并将自身的信息传送到网络中。
(2)估算平均跳距
用锚节点间坐标之差除以锚节点间的跳数求得检测区域内所有锚节点间的平均跳距HopSizeij为
(1)
式中:(xi,yi,zi)、(xj,yj,zj)分别为锚节点i、j的位置坐标,hij为锚节点i和锚节点j之间的跳数。进一步可得出未知节点与锚节点i之间距离di为
di=hij×HopSizeij,(i≠j)
(2)
(3)计算未知节点位置
最后,经过以上计算后,若未知节点附近的邻居锚节点数等于4个,倾向于选择四边测量法获得未知节点的坐标。若未知节点附近的邻居锚节点数超过4个,倾向于选择极大似然估计法获得未知节点的坐标。
2 算法改进思想
本文的改进算法具体介绍如下:
2.1 分层式锚节点组移动路径
在三维空间中,节点部署杂乱无序。为了定位计算容易,将三维空间分层为无数个二维空间进行处理。三维空间的分层式划分如图1所示。
监测区域经过分层处理后,在监测区域边界处部署一组移动锚节点组,并使锚节点组按一定的静态移动路径移动。其中,移动锚节点组的相对位置关系如图2所示。
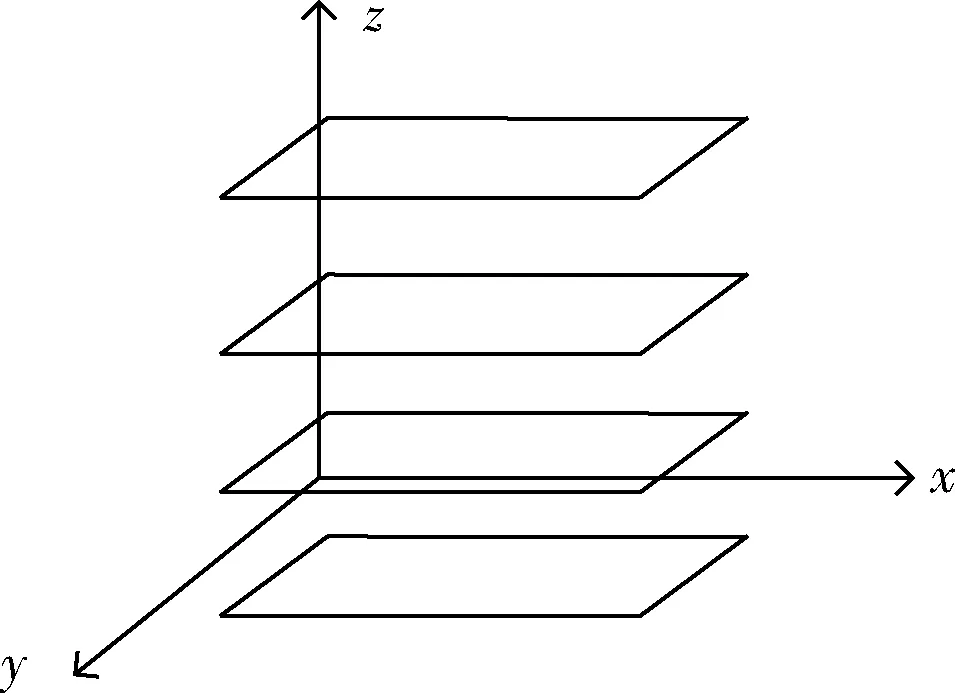
图1 三维空间的分层式划分
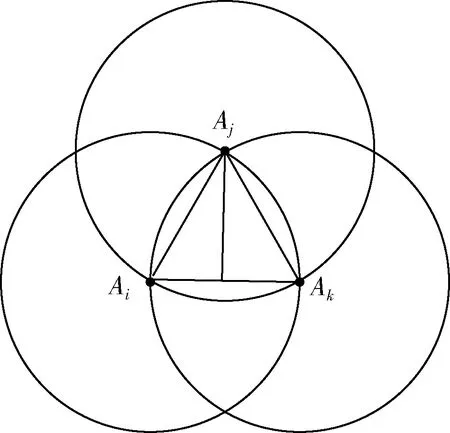
图2 移动锚节点组的相对位置关系

接下来,让锚节点组在监测区域内按规定的移动路径开始移动,如图3所示。

图3 锚节点组移动路径

2.2 计算锚节点共面度值
为了解决共面现象导致未知节点不能确定的问题,必须要采取一些度量标准衡量四面体的质量。现有的衡量四面体质量的标准有系数γ、半径比ρ、最小立体角θ等,考虑到衡量四面体网格质量标准方法的准确性几乎等价,本文采用最小立体角θ的测量方式测量共面度,具体介绍如下:
在4个锚节点构成的四面体中,4个夹角分别用θ1、θ2、θ3、θ4表示,具体计算如式(3)所示
(3)
式中:V表示四面体的体积,lij表示锚节点i、j之间的距离。将θ1、θ2、θ3、θ4这4个角度进行对比,取其中的最小角度θ作为衡量四面体的平面度值,如式(4)所示
θ=MIN(θ1、θ2、θ3、θ4)
(4)

(5)
2.3 虚拟锚节点组平均跳距
3D-DV-Hop定位算法是用平均跳距等于锚节点间距离除以锚节点间跳数。但在本文中提出的锚节点组按规定路径移动的三维定位算法中,锚节点组是按静态移动路径SCAN移动整个三维区域,遍移动后的区域中不存在锚节点,且未知节点所获得信息均来源于虚拟锚节点并非锚节点。因此,无法直接计算锚节点间的平均跳距。
接下来,用一种计算虚拟锚节点组间的距离方法解决移动路径中存在的问题,即用筛选出来的r组虚拟锚节点组来估算平均每跳距离,如式(6)所示

(6)
2.4 未知节点位置重新定位
最后,将节点之间的距离进行共面度加权处理,如下式(7)所示
(7)
式中:(x,y,z)表示待定位节点坐标,(xn,yn,zn)表示虚拟锚节点组的位置,wi表示平面度加权值,di(i=1,2,…,n)表示节点间的距离。
将式(7)化简后可得
AX=b
(8)
其中
(9)
(10)
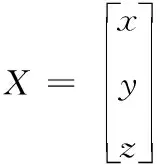
(11)
最终求得未知节点的坐标为
X=(ATA)-1ATb
(12)
3 仿 真
为验证提出的移动锚节点组按规定移动路径移动的定位算法能够有效降低节点定位误差,本文对算法进行了仿真,并与3D-DV-Hop算法以及其它的改进算法进行比较。仿真中,平均定位误差的衡量标准如式(13)所示
(13)
式中:待定位未知节点的实际坐标用(xi,yi,zi)表示,待定位未知节点的所求坐标用(xj,yj,zj)表示,监测区域内待定位未知节点的数量用N表示,监测区域内节点的通信范围半径用R表示。相关的仿真参数见表1。

表1 仿真参数
将通信半径R为40 m的500个节点随机抛洒在100 m*100 m*100 m的监测区域内,节点随机抛洒生成图如图4所示。其中,锚节点为100个,符号为“*”,未知节点400个,符号为“∘”。
为了仿真结果的可靠性,对节点随机分布进行500次仿真,仿真的相对平均误差如图5所示。由500次仿真结果可知,除了个别次仿真外,改进算法的定位误差均在0.21 m上下浮动,定位误差较稳定。

图4 未知节点定位误差
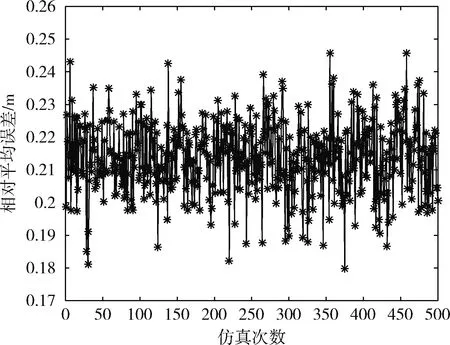
图5 loop次相对平均误差
图6为锚节点比例对平均定位误差的影响仿真图。仿真中,设监测区域为边长100 m的三维空间,在监测区域内随机分布500个节点,且节点通信半径固定为40 m,改变网络中锚节点的比例,从10%逐步增加到40%,同时对本文算法、传统算法、文献[10]算法以及文献[11]算法进行仿真对比。
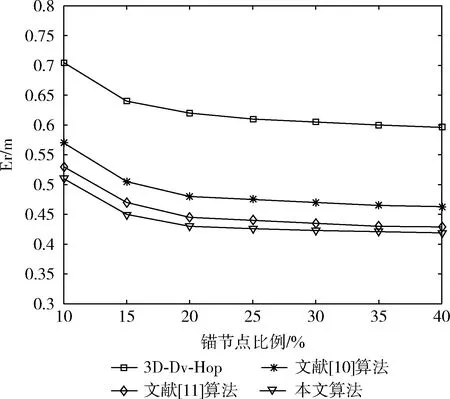
图6 锚节点比例对平均定位误差的影响仿真
根据图6中的数据线变化能够看到,当锚节点数达到总节点数的20%以上时,节点定位误差变化开始缓慢。4种算法平均定位误差随着锚节点的比例增大均有所下降,本文算法的平均定位误差相对于传统定位算法、文献[10]算法、文献[11]算法分别降低了29.76%、10.22%、4.31%。
图7为节点通信半径对平均定位误差的影响仿真图。网络中总节点为500,锚节点比例为20%,让节点通信半径逐渐递增,对算法进行仿真。

图7 节点通信半径对平均定位误差的影响仿真
从图7中的数据线变化可以明显看出当节点通信半径达到40 m时,节点定位误差的变化开始平缓。4种算法的平均定位误差随着通信半径的增大均有明显下降,本文算法的平均定位误差相对于传统定位算法、文献[10]算法、文献[11]算法分别降低了37.26%、13.85%、8.96%。
图8为总节点个数对平均定位误差的影响仿真图。在监测区域中分别部署100个、200个、300个、400个、500个节点,网络中锚节点占比固定为总节点的20%,节点通信半径固定为40 m,对算法进行仿真。

图8 总节点个数对平均定位误差的影响仿真
从图8中可以看出,传统定位算法、文献[10]算法、文献[11]算法以及本文提出的定位算法随着总节点个数的增加,平均定位误差都有所下降。在同等总节点个数情况下,本文提出的定位算法的平均定位误差相对于传统定位算法、文献[10]算法、文献[11]算法分别降低了36.25%、12.77%、16.83%。
4 结束语
当三维空间中锚节点组出现共面现象时,将会导致未知节点无法定位。针对这个现象,提出一种适用于三维空间中的锚节点组按规定路径移动的非测距定位算法。通过对监测区域进行分层式锚节点组移动路径规划,计算虚拟锚节点组的共面度值以及用虚拟锚节点组计算平均跳距,最终对节点间距离进行共面度加权计算出待定位节点位置。实验结果表明本文提出的算法有效的避免了锚节点共面现象,进而提高了未知节点的定位精度。接下来的工作是针对算法中存在的共线问题进行研究。
