基于并行匹配的RFID自适应碰撞树算法
2020-09-04贺晓霞贾小林
贺晓霞,贾小林
(西南科技大学 计算机科学与技术学院,四川 绵阳 621000)
0 引 言
射频识别(radio frequency identification,RFID)技术是实现物联网(IoT)对象感知的关键。在RFID系统中当多个标签试图同时响应阅读器的询问时,就会发生标签碰撞,即阅读器无法识别任何标签[1]。这种碰撞不仅延长了标签识别的时间,而且增加了阅读器的能耗。因此有效地解决标签碰撞的防碰撞算法对于大规模物联网RFID系统的开发具有重要意义。标签防碰撞算法主要可以分为3大类:基于ALOHA的算法[2]、基于树的算法[3]和混合算法[4]。基于ALOHA的算法在标签数量相对较少的情况下表现较好的性能,但是随机机制又会导致“标签饥饿”[5]。基于树的算法的优点是即使在标签密集的RFID系统中也能成功识别出所有的标签。
基于Manchester code的位跟踪技术在基于树的算法中得到了广泛的应用,如碰撞树算法(CT)[6]、双时隙碰撞跟踪树算法(BSCTTA)[7]、双前缀探针算法(DPPS)[8]等。BSCTTA的设计使得前缀开销和迭代开销可以通过时间分割响应[7]来减少,但标签数量非常大时,该算法性能会降低,因为它只会在发生碰撞时分成两个子组来避免标签冲突[9]。自适应碰撞树算法(ACT)[10]是一种基于碰撞树算法(CT)和改进的碰撞树算法(ICT)[11]的防碰撞算法。ACT在一定程度上缩短了标签识别时间,提高了系统性能,但在使用四叉树搜索时,它增加了空闲周期的数量,对系统性能产生了影响。类似,AdATSA[12]和OBTT[13]在识别过程中仍然存在空闲时隙,不可避免地也降低了系统性能。
基于上述问题,本文提出了一种基于并行匹配方案的自适应碰撞树(PACT)算法,通过引入并行匹配机制来减少空闲的查询周期,同时利用碰撞标签的数量自适应地选择搜索模式(2-branchCT还是8-branchCT),大大降低搜索深度,减少碰撞周期和延迟。
1 PACT算法
(1)并行匹配与系统传输模型
在查询树算法(QT)中,当阅读器在识别过程中检测到了碰撞时,通过将0和1附加到之前的前缀生成一个新的前缀并入栈,然后逐个发送两个查询。具有与前缀匹配的ID的标签将响应除了其ID的匹配部分之外的完整部分。在本文中,将这种查询类型称为串行匹配查询,指定为SMQ(sequential matching query)。与之相比,本文提出的算法只需要发送一个查询,但是并行执行标签匹配。这种冲突仲裁称为并行匹配方案,使用的查询称为并行匹配查询,简称PMQ(parallel matching query)。具体来讲,由于标签ID的二元确定性原则[11],与前缀匹配的标签肯定会在两个时隙中的一个中响应。在识别过程中,与前缀匹配的标签将在两个连续时隙之一中发送它们的ID,标签通过其ID的第(L+1)位的值是0还是1来确定应响应的时隙数量,其中L是所接收的前缀的长度。在第一个时隙中分配的标签先发送其ID,然后在第二个时隙中分配的标签将在第一个时隙上的传输完成后再发送其ID。使用这种机制不仅有效地减少了查询周期的数量,而且减少了阅读器发送的查询前缀的长度。如图1所示,是传统基于树的算法和并行匹配方案的链路时序。阅读器在时间TR中发送CW信号和查询命令。标签从射频信号中获取工作能量并传输信息。在接收到阅读器的命令之后,标签在时间T1中生成它们的响应。

图1 基于传统的树算法和并行匹配方案的链路时序
根据上述传输模型,时间模型描述如式(1)所示。在询问区中识别n个标签所花费的总时间为每个循环中阅读器发送查询的时间加上标签响应所需的时间。令CPMQ和CSMQ分别表示PMQ和SMQ的个数。识别时间可以表示为下式:其中TRi和Ttagi分别表示在第i个周期中阅读器传输查询和标签响应所花费的时间
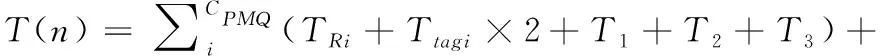
(1)
(2)自适应分割机制
所提出的算法采用自适应分割机制来根据碰撞条件决定CT的选择为8分支碰撞树或2分支碰撞树。假设在系统中有N个标签待识别,分布的子分支的数量是L,搜索深度是k。则识别概率可以计算为
p(k)=p(1)*(1-p(1))k-1
(2)
p(1)=(1-1/L)N-1
(3)
然后我们可以得到搜索深度的数学期望,即

(4)
因此,标签识别所需的平均时隙数是
(5)
对于式(5)中的L进行部分推导,可以得到
(6)
从式(6)可以观察到,当分布的子分支的数量L等于标签的数量N时,系统所需的时隙数最少。因此,当标签数量很多时,为了减少识别所需的时隙,可以分配更多子分支。
根据式(5),将L=2代入到式中,则2-branch树中识别过程所需的平均时隙数可以表示为
T2branch=2/(1-1/2)N-1=2N
(7)
在8-branch树中,所需的平均时隙数为
T8branch=8/(1-1/8)N-1=8N/7N-1
(8)
通过等式(7)和式(8)可以看到,当N≥4时,T8branch
(3)识别过程
PACT算法使用两种类型的查询,SMQ和PMQ,初始化查询类型为PMQ,前缀为‘ε’。标签响应的长度由查询类型决定,其中k为标签ID的长度,L为接收前缀的长度,如式(9)
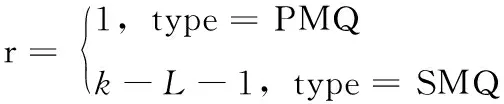
(9)
PACT算法描述如下:具体来说,Prefix是前缀堆栈。M和N分别是碰撞比特的数量和碰撞标签的数量。Request(ε)要求所有在阅读器查询范围内的标签响应。Request(prefix)要求标签将自己的ID与阅读器发送的前缀进行比较,如果满足查询条件(假设前缀和标签ID的长度分别为L和k),则将剩余的(k-L)位返回给阅读器。PACT算法详细过程的伪代码见表1。

表1 PACT算法详细描述
2 性能分析
在本节中,通过理论分析,从时间复杂度和系统效率两个方面对PACT的性能进行了评估,通过测量所需的时隙来评估系统的时间复杂度。
设n是读取器天线范围内的标签数量,d是标签ID的长度。C8branch(n) 表示在8-branch树搜索中产生的碰撞时隙的数量,C2branch(n) 表示在2-branch树搜索中产生的碰撞时隙的数量。考虑到自动识别的思想,当一个比特发生N1次碰撞时,系统可以减少2N1时隙。
因此,总时隙数可以计算为
T(n)=C8branch(n)+C2branch(n)+n-2N1
(10)

在文献[14]中,给出了完全二进制树中碰撞时隙数的理论期望
(11)
其中,L为树的搜索深度,B为树的维数。因此,当L=k+1时,8分支树搜索的碰撞时隙为
(12)
根据文献[4],2分支树搜索中的碰撞时隙数与B分支树搜索中的碰撞时隙数之比约为1/log2B。 由于2-branch CT中的碰撞节点数是(n-1)[11],完全8-branch CT中的碰撞节点数应该是 (n-1)/3, 假设要识别的系统中有n个标签。可以得到在PACT中8-branch树搜索中产生的碰撞周期的数量为
(13)
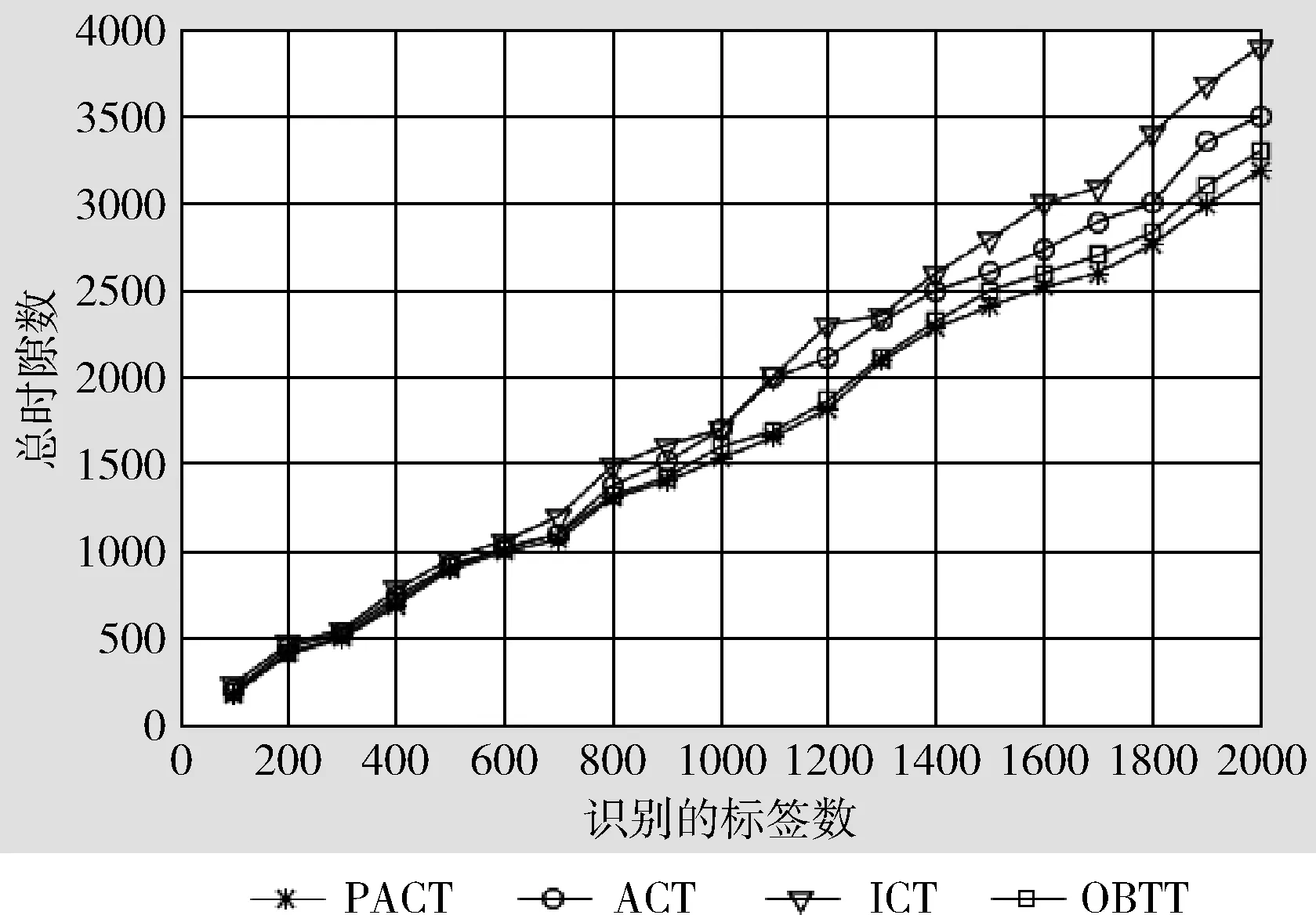
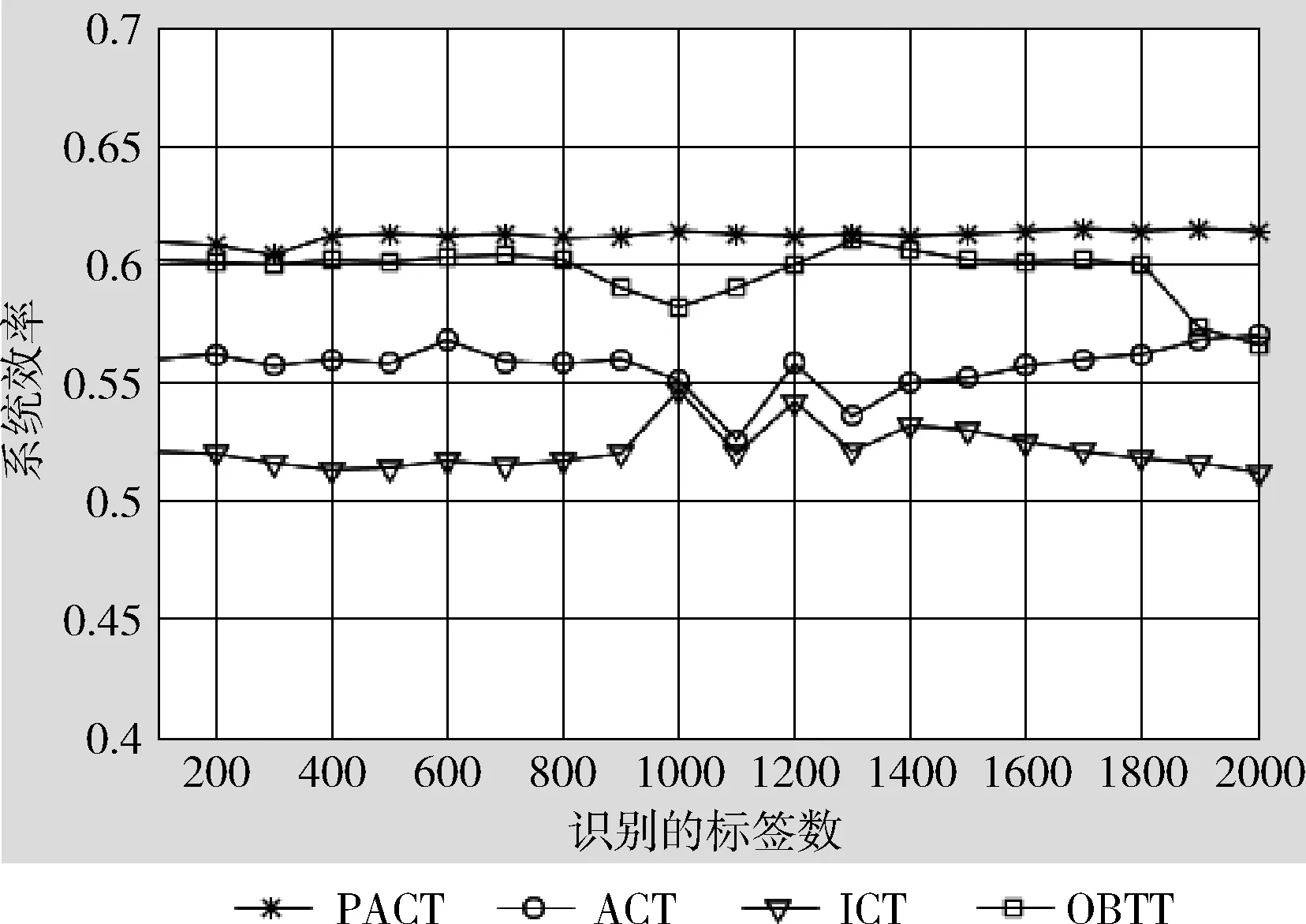
综上所述,当搜索深度等于k+1时,每个2-branch CT中剩余的碰撞时隙中只有两个或3个标签1 (14) 因此,PACT中所需的总时隙数可以计算为 (15) 系统效率定义为标签数量与在系统中识别它们所需的总时隙数量之比。因此,我们可以获得系统效率为 (16) 本文利用MATLAB仿真平台,选择理想信道,将本文提出的PACT算法与自适应碰撞树算法(ACT)、改进的碰撞树算法(ICT)以及最优的跟踪树算法(OBTT)分别在所需时隙的数量、碰撞时隙的数量以及系统效率方面进行分析比较。假设系统内标签均匀分布,遵循ISO18000-6标准,随机生成编号长度为96位的电子标签,标签数量从100增加到2000。 图2显示了标签数量与识别过程中所需的总时隙数之间的关系。可以看出,在相同数量的标签下,本文提出的PACT算法所需的时隙数小于其它3种算法(ACT,ICT和OBTT)所需的时隙数。 图2 总时隙数与标签数关系 图3描绘了碰撞时隙数与标签的关系图。当标签的数量小于200时,OBTT和PACT生成的碰撞时隙的数量是相似的,但是随着标签数量增加,PACT生成的碰撞时隙的数量明显低于其它3种算法。主要是因为在PACT中使用了并行匹配方案使得8分支树搜索阶段减少了大量的碰撞时隙。 图3 碰撞时隙数与标签数关系 图4为4种算法的系统效率对比。很明显,PACT的系统效率约为0.609,高于其它3种算法。ICT,ACT和OBTT的平均系统效率分别为0.521,0.559和0.601。 图4 系统效率与标签数关系 本文提出一种基于并行匹配方案的RFID自适应碰撞树算法(PACT),该算法使用并行匹配方案来减少查询周期的数量,同时利用冲突标签的数量来自适应地选择搜索模式,当标签数大于等于4时,PACT算法选择使用8-branch CT,在标签数小于4时则使用2-branch CT。PACT的系统效率约为0.6092,也表现出了较好的稳定性。仿真结果表明,所提出的算法与现有的基于树的算法相比,不仅提高了系统的效率和标签识别的速度,而且降低了时间复杂度,特别是在大规模标签情况下。
3 仿真结果

4 结束语
