基于牛顿三次插值的自适应差分进化算法

陈恩茂，徐志刚，付 源

(1.东北大学 机械工程与自动化学院，辽宁 沈阳 110819；2.中国科学院沈阳自动化研究所，辽宁 沈阳 110016；3.中国科学院机器人与智能制造创新研究院，辽宁 沈阳 110169；4.湖南大学 机械与运载工程学院，湖南 长沙 410082)

0 引 言

差分进化(differential evolution，DE[1])算法自提出以来，由于其结构简单、鲁棒性强、收敛速度快等特点，被广泛应用于各工程领域[2]。本文提出一种基于牛顿三次插值的自适应差分进化算法(adaptive differential evolution algorithm based on Newton cubic interpolation，ANCIDE)。该算法的改进特点如下：设计局部搜索半径，在最优个体附近搜索4个节点运用牛顿三次插值进行局部搜索，提高算法收敛性能；提出自适应论证策略，根据当代运用牛顿三次插值的效果来调整下一代使用牛顿三次插值的概率，避免陷入局部最优；采用自适应学习策略控制F和CR，解决参数设置敏感的问题。

1 经典差分进化算法

步骤1 种群初始化。DE随机产生NP个D维个体[3]

(1)

(2)

式中：NP表示种群数量，D表示个体维度，rand(0,1)代表(0,1)内服从均匀分布的随机数。

步骤2 常见的变异策略有DE/rand/bin/1和DE/best/bin/1，分别如式(3)和式(4)所示[4]

Vr,G=Xr1,G+F·(Xr2,G-Xr3,G)

(3)

Vr,G=Xbest,G+F·(Xr2,G-Xr3,G)

(4)

式中：r1,r2,r3是3个不同的随机数，且r1≠r2≠r3≠i。G表示第G代个体。Xbest,G表示第G代最优个体。Vr,G表示第G代变异个体。F是缩放因子，用来控制差分向量。

步骤3 交叉操作。对目标个体Xi,G和变异个体Vi,G进行交叉操作，产生实验个体Ui,G，即

(5)

式中：CR为交叉概率，rand(0,1)为(0,1)内服从均匀分布的随机数，jrand为[1,D]的随机整数。

步骤4 选择操作。DE采用贪婪算法来选择适应值较小的作为进入下一代种群的个体。即

(6)

2 ANCIDE算法

2.1 牛顿三次插值

在区间[a,b]上f(x)关于两个不同的节点xi，xj的一阶差商定义如下[5]

(7)

在区间[a,b]上f(x)关于3个不同的节点xi，xj，xk的二阶差商定义如下

(8)

一般地，称式(9)为f(x)关于k+1个不同的节点

x0,x1,…,xk的k阶差商

(9)

根据差商的定义，牛顿插值多项式表示为

Nn(x)=f(x0)+f[x0,x1]ω1(x)+
f[x0,x1,x2]ω2(x)+…+f[x0,x1,…,xn]ωn(x)

(10)

式中：ωn(x)=(x-x0)(x-x1)…(x-xn-1)。特别地，当选择4个不同的节点进行插值时，得到的Nn(x)为牛顿三次插值多项式。与牛顿二次插值相比，牛顿三次插值选取节点更多，拟合曲线更接近函数图像，插值精度更高。在第j维空间进行牛顿三次插值时，式(10)可以改写为

(11)

式中

a=f[x0,j,x1,j,x2,j,x3,j]

(12)

b=f[x0,j,x1,j,x2,j]-
f[x0,j,x1,j,x2,j,x3,j](x0,j+x1,j+x2,j)

(13)

c=f[x0,j,x1,j]-f[x0,j,x1,j,x2,j](x0,j+x1,j)+
f[x0,j,x1,j,x2,j,x3,j](x0,jx1,j+x0,jx2,j+x1,jx2,j)

(14)

d=x0,j(f[x0,j,x1,j,x2,j]x1,j-f[x0,j,x1,j]-
f[x0,j,x1,j,x2,j,x3,j]x1,jx2,j)+f(x0,j)

(15)

如图1和图2所示，a、b、c共同影响局部最优点x4,j的位置。

图1 a≠0时x4,j的搜索方向

图中，x0,jx*,j′。根据x4,j的搜索方向，将求解x4,j的公式总结如下

(16)

图2 a=0时x4,j的搜索方向

式中：r1、r2、r3、r4为(0,1)内服从均匀分布的随机数。

2.2 运用牛顿三次插值局部搜索

2.2.1 局部搜索半径

在第j维空间对最优个体xbest,j附近运用牛顿三次插值进行局部搜索。其中搜索半径R、R′分别定义为

R=[max(xj)-min(xj)]·r

(17)

R′=[max(xj)-min(xj)]·r′

(18)

式中：max(xj)和min(xj)分别代表种群内所有个体在第j维空间xj的最大值和最小值，r和r′分别代表两个不同的(0,1)的随机数。由此可得除xbest,j外，其余3个插值节点为

x0,j=xbest,j-R

(19)

x1,j=xbest,j+R

(20)

x2,j=xbest,j-R′

(21)

2.2.2 自适应论证策略

为了评估是否在下一代运用牛顿三次插值在最优个体附近进行局部搜索，定义牛顿插值率(Newton interpolation rate, NIR)如式(22)表示[6]

(22)

式中：f(xbest)和f(xbest′)分别代表当代最优个体的适应值和使用牛顿三次插值得到最优个体的适应值。NIRmax表示牛顿插值率的最大值，NIRmin表示牛顿插值率的最小值。式(22)表明，如果使用牛顿三次插值进行局部搜索有效，则提高下一代使用牛顿三次插值的概率。反之，则降低使用牛顿三次插值的概率。

2.3 自适应学习策略控制参数

缩放因子F和交叉概率CR对DE的性能至关重要。F选择较大的值、CR选择较小的值可以提高DE的全局搜索能力；F选择较小的值、CR选择较大的值可以提高DE的局部搜索能力，加速收敛。变异操作阶段，采用如下方案[7]调整F的值，并应用到DE/best/bin/1中

Fi=randcauchy(μF,0.1)

(23)

式中：randcauchy表示位置参数为μF，尺度参数为0.1的柯西分布函数。当Fi≥1时，Fi=1；当Fi≤0时，Fi根据式(23)重新计算。μF在积累每代成功进化个体的缩放因子F后如式(24)更新

μF=(1-c)·μF+c·meanL(SF)

(24)

式中：c∈(0,1]，SF为成功进化个体缩放因子F的集合。meanL()为Lehmer平均数，如式(25)计算

(25)

交叉操作阶段，每个个体的交叉概率CRi根据式(26)进行更新

CRi=randni(μCR,0.1)

(26)

式中：randni表示数学期望为μCR，标准差为0.1的高斯分布函数。当CRi>1或CRi≤0时，CRi根据式(26)重新计算。与μF类似，μCR在积累每代成功交叉个体的交叉概率CR后如式(27)更新

μCR=(1-μ)·μCR+c·meanA(SCR)

(27)

式中：c∈(0,1]，SCR为成功交叉个体的交叉概率CR的集合。meanA()为算术平均数，如式(28)计算

(28)

2.4 ANCIDE算法步骤

总结以上改进策略，得到以下ANCIDE算法步骤：

步骤2 评估初代最优个体xbest及其对应的最优适应值f(xbest)。并置当前迭代次数G=1，当前函数访问次数FEs=NP。

步骤3 判断是否满足终止准则，如果满足，则输出当前最优个体作为最优解；否则转步骤4。

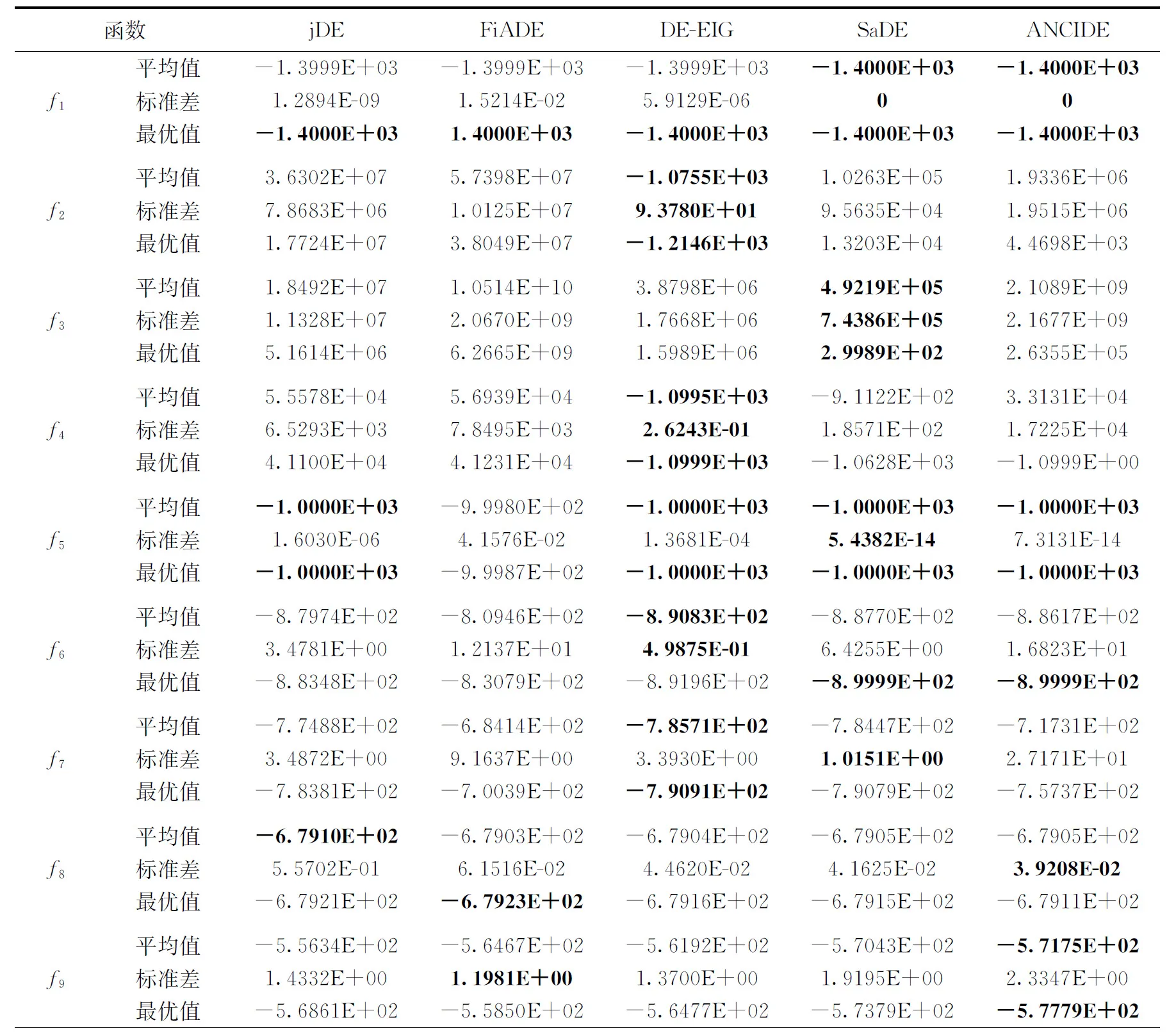
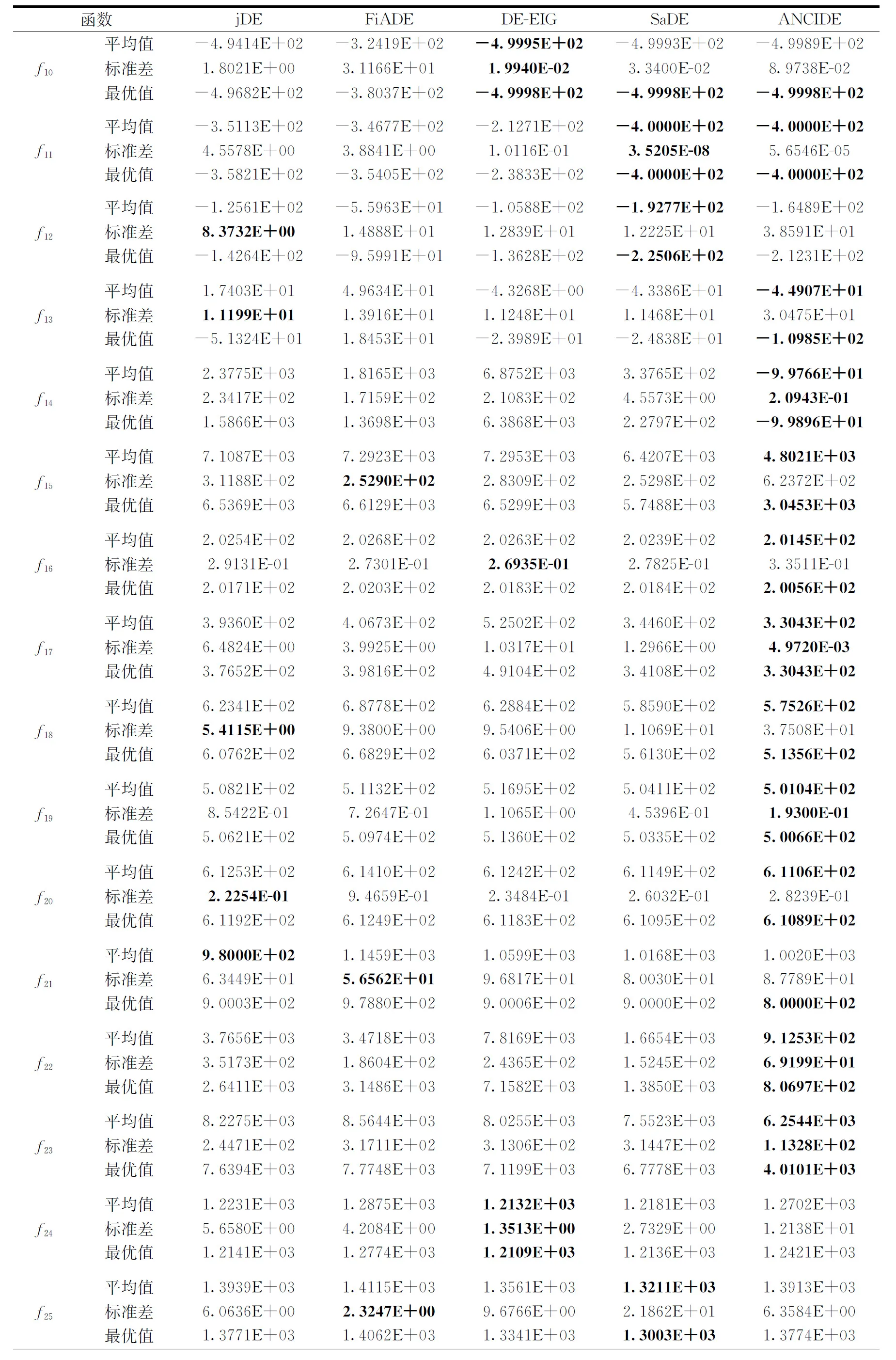
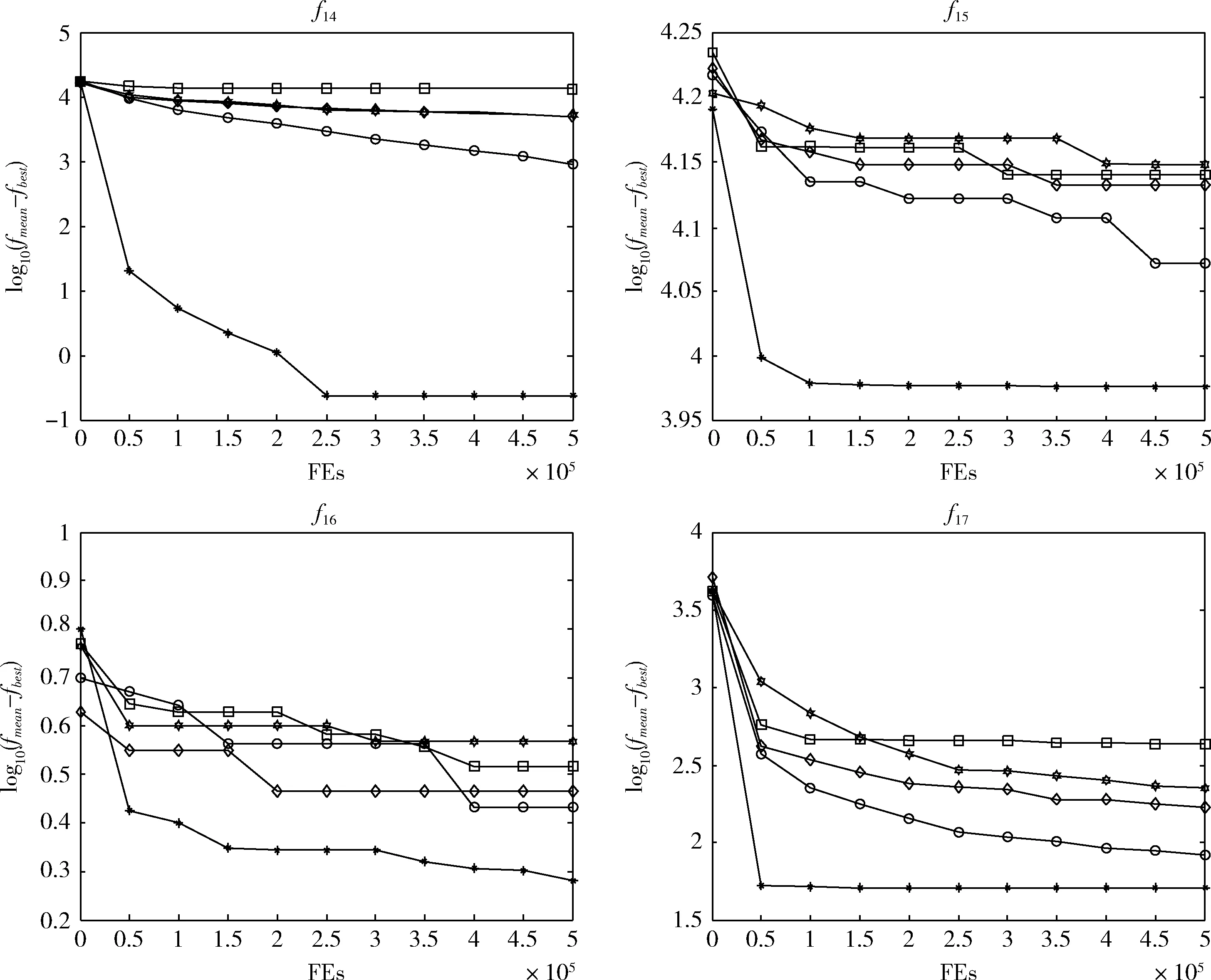
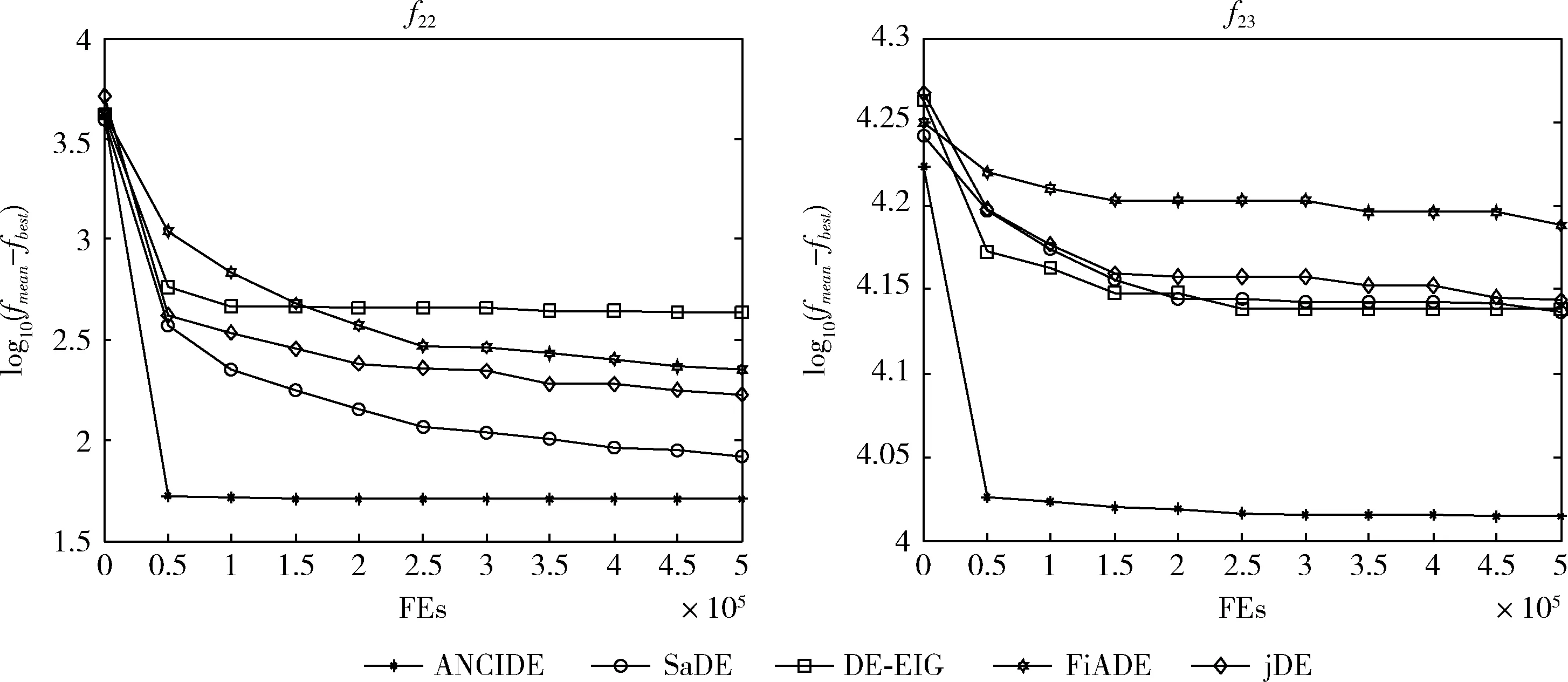
步骤4 若随机数rand(0,1)

步骤5 在每个维度利用步骤4所求的4个插值节点xbest,j、x0,j、x1,j、x2,j分别根据式(12)、式(13)、式(14)、式(15)计算牛顿三次插值多项式及a、b、c、d。

步骤6 根据式(16)计算牛顿三次插值得到最优个体xbest′及其对应的适应值f(xbest′)， 若f(xbest′)

步骤7 对每个个体根据式(23)计算Fi，根据式(4)进行变异操作，并得到变异个体Vi。

步骤8 对每个个体根据式(26)计算CRi，根据式(5)进行交叉操作，并得到实验个体Ui。

步骤9 对每个个体根据式(6)进行选择操作，若f(Ui,G)

3 数值实验及结果分析

3.1 基准测试函数

选取CEC2013上的由28个基准函数组成的测试集[8]进行算法测试。在这28个基准测试函数中，f1～f5为单峰函数，用于考察算法的收敛速度和收敛精度；f6～f20为多峰函数，局部最优点的数量随维度指数递增，用于考察算法的全局搜索能力；f21～f28为组合函数，通过将单峰函数和多峰函数组合，增大算法的搜索难度。

3.2 实验结果及分析

为了验证ANCIDE的可行性和有效性，与著名的jDE[9]、FiADE[10]、SaDE[11]、DE-EIG[12]进行测试比较。为保证实验的公平性，每个算法的种群规模NP取4D，函数最大访问次数FEsmax取10^4*D，均在处理器为Intel(R) i5-7500，内存为8 GB的计算机上，通过Matlab R2014a独立运行30次。表1为各算法参数初始值，表2为30维下各算法的实验结果(表中加粗部分为最优解)。

表1 各算法参数初始值

表2 30维运行结果

表2(续)

表2(续)

由表2分析可知，对于单峰函数f1,f5，大部分多峰函数f9,f13,f14,f15,f16,f17,f18,f19,f20，及组合函数f22,f23，ANCIDE算法收敛精度更高，更易找到全局最优点。尤其是对于多峰函数如f14,f15,f16,f17，组合函数如f22,f23, ANCIDE算法的竞争力十分显著(如图3所示)。因此，ANCIDE算法不失为一个解决复杂优化问题的好方法。

图3 30维各算法的收敛曲线

4 结束语

经典差分算法存在易早熟收敛、对参数设置敏感的问题。为解决这些问题，本文提出基于牛顿三次插值的自适应差分进化算法。利用牛顿三次插值拟合目标函数图像，为算法局部搜索提供方向，从而加快算法收敛速度；为了平衡全局搜索和局部搜索，设计自适应论证策略来评估下一代是否使用牛顿三次插值；采用自适应学习策略来调整缩放因子F和交叉概率CR，从而避免人为设置参数。实验结果表明，对于大部分基准函数，该算法的性能均优于其它改进DE算法。今后的研究方向将致力于继续提高算法性能和解决实际工程问题。