多径衰落信道下的单载波调制识别算法

杨 洁，吴凤杰

(西安邮电大学 通信与信息工程学院，陕西 西安 710121)

0 引 言

自动调制识别(automatic modulation recognition，AMR)是认知无线电、信号检测、干扰识别、电子战等领域的一个重要组成部分。现有的AMR方式大都假定信号被加性高斯白噪声污染，致使采用传统的基于瞬时特征[1]、小波变换[2]、支持向量机[3]等的识别方法不再适用于多径衰落信道的环境。

针对上述问题，文献[4]引入八阶累积量构造特征参数，文献[5]利用各阶累积量作为深度神经网络的输入，实现了对信号的整体可分，但复杂度较大；文献[6,7]构造了平坦衰落信道下的二阶、四阶和六阶循环累积量特征；文献[8]通过估计信道模型，利用四阶循环累积量，实现对相位键控(phase-shift keying，PSK)和正交幅度(quadrature amplitude modulation，QAM)信号的分类识别；文献[9]提出基于累积量和循环累积量的组合特征，仿真结果表明，其在衰落信道中对载频频偏、相位偏移等损伤具有较好的鲁棒性。

以上提到的算法所构建的特征均基于二阶和四阶及更高阶的循环累积量，未能很好利用其它相关累积量。基于此问题，首先对接收信号进行零均值处理，随后估计各接收信号的三阶和四阶循环累积量，将四阶循环累积量作为归一化因子，得到一组差异较大的特征向量，最后利用鲸鱼算法对支持向量机(support vector machine，SVM)进行参数寻优，利用优化后的分类器对幅度键控(amplitude-shift keying，ASK)、PSK、QAM这3类信号进行识别，在多径衰落信道条件下取得了较好的分类效果。

1 信号模型

假设调制信号经过多径衰落信道后，存在载频偏差、相位偏差、定时偏差以及加性高斯白噪声和多径数量的影响，其接收信号可以表示为

(1)

其中，L为多径信道数量，hl为信道的衰减系数，φl为信道相位偏差，Δf为载波频率偏差，τl为定时偏差，ω(t)为均值为0的加性复高斯白噪声，且与发送信号相互独立，s(t)为调制信号，其表达式如式(2)所示

(2)

(3)

(4)

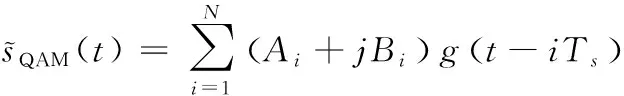
(5)

其中，Ai，Bi为基带信号幅度，M为调制进制，S为信号功率，φi为信号调制相位，g(t)为矩形脉冲波形，Ts为符号间隔，N为码元个数。

2 特征提取

2.1 循环累积量理论

通信信号通过将传输的基带信号调制到周期信号的某个参数上，如对正弦载波的幅度、相位和频率进行调制，从而产生具有周期平稳性的随机调制信号。而在非合作通信中，由于传输信道以及其它非理想情况，导致接收信号出现不同程度的畸变，从而导致基于瞬时特征等的调制算法效能降低。循环平稳信号作为一种特殊的非平稳信号，其高阶循环累积量理论上可以抑制任何平稳或非平稳噪声，且可以恢复时变相位信息，适用于衰落信道中信号特征的提取。故可以利用高阶循环统计量来表征单载波调制信号的相关特征。

对于一个零均值的循环平稳实信号x(t)，定义其k阶滞后积期望值为

(6)

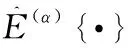
对于固定的滞后偏差τ1,…,τk-1，如果mk(t;τ)存在一个相对于时间t的Fourier级数展开，则有

(7)

(8)

则在分时概率分布条件下可以定义信号x(t)的循环矩为

Mx(α,τ)k,δ=x(*)1(t)x(*)2(t+τ1)…x(*)k(t+τn-1)e-jαt

(9)

式中：(*)u，u=1,…k表示对信号进行共轭变换，且δ表示共轭变换次数。

则可得信号的k阶循环累积量为

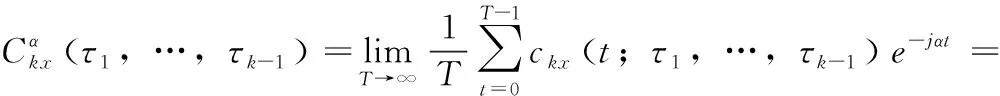
(10)

其中，ck(t;τ)表示时变累积量，定义如下

ckx(t;τ)=cum[x(t),x(t+τ1),…,x(t+τk-1)]

(11)

式中：cum[.]表示特征函数围绕原点的Taylor级数展开式中的系数。

通过矩累积量转换关系，可以利用较低阶的循环矩表示高阶的循环累积量，如式(12)所示

(12)

2.2 接收信号的循环累积量特征

由上述分析可得，对于一个零均值的循环平稳随机过程x(t)，其三阶循环累积量相对于偶次高阶矩和二阶循环累积量能更好抑制高斯噪声，则

(13)

当τ1=τ2=0时，且由于循环累积量具有可加性，则对于通信调制信号有

(14)

当高斯白噪声循环累积量阶数大于2时其理论参考值等于零。由于不同传输路径相互独立，各传输码元相互独立，故可得接收信号循环累积量为

(15)

其中，单径循环累积量计算如式(16)所示

(16)

当选取循环频率α=fc时，则有

(17)

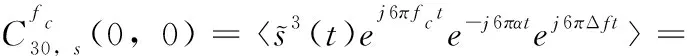
(18)

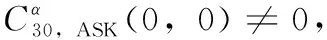
由式(6)～式(12)可推导信号的四阶循环累积量[10]，如式(19)所示

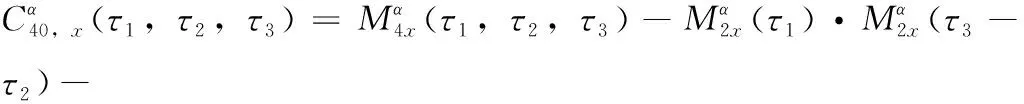
(19)

当τ1=τ2=τ3=0时

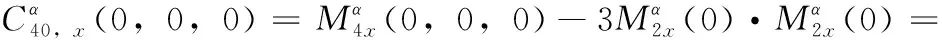
(20)

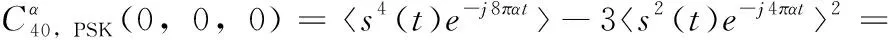
(21)

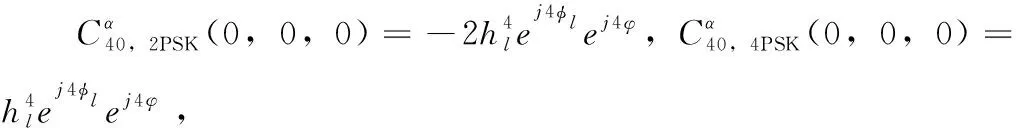
(22)

由以上分析可得，特征向量Fx能够有效消除多径衰落信道对信号产生的影响。

3 分类器设计

3.1 支持向量机

SVM是一种基于统计学习理论的小样本机器学习算法，相比于传统的神经网络算法具有更好的泛化性和鲁棒性，可以有效解决模式识别中的诸多问题。SVM基本思想是在训练样本空间中寻找一个超平面，使其能够最大限度的将样本区分开来，且可以保证具有最好泛化性能[11]。

假定训练样本集为{(xi,yi)},yi∈{-1,+1}，存在一个超平面Tx+b=0，使得式子(Tx+b)yi≥1成立，则将式等于1的样本点称作为支持向量，即求解,b使向量到超平面的距离最大。则可得SVM的基本模型如式(23)所示

(23)

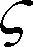
(24)

对式(24)求偏导代入式(23)可得对偶问题为

(25)

式中：T表示转置，求解式(25)得到相应参数代入式(26)从而得到最优超平面

f(x)=Tx+b

(26)

当存在原始训练空间线性不可分时，通过引入核函数k(·,·)将其映射到一个高维空间从而实现线性可分，则定义核函数为

k(xi,xj)=ρ(xi),ρ(xj)=ρρ(xj)

(27)

ρ(x)为高维特征向量。选取高斯核函数映射原始空间，如式(28)所示

(28)

3.2 鲸鱼优化算法

WOA是在2016年提出一种基于模拟座头鲸捕食原理的元启发式算法，相较与传统的优化算法其性能相对较高[11]。则WOA算法模型为

D=|FX*(t)-X(t)|

(29)

X(t+1)=X*(t)-A·D

(30)

式中：X(t)为鲸鱼当前位置，X*(t)为第t次迭代的最优解位置，其A,F分别为

A=2a·r-a,a∈[0,2]

(31)

F=2r

(32)

式中：r为[0,1]之间的随机数，a会随着迭代过程呈线性下降。

鲸鱼位置则由式(33)进行更新

(33)

式中：D′=|X*(t)-X(t)|表示鲸鱼到猎物的距离，b′为常数，l′∈[-1,1]是一个随机数，p∈[0,1]表示随机概率。

为加强全局搜索能力，选用一个随机位置来更新鲸鱼位置

D=|FXrand(t)-X(t)|

(34)

X(t+1)=Xrand(t)-A·D

(35)

当A≥1时随机选取位置Xrand进行更新。

为提高WOA算法的搜索速度，先采用网格式交叉验证(k-fold cross validation，K-CV)寻优方法进行粗略寻找，之后采用WOA算法在此基础上精确查找。

4 仿真验证

文中考虑{ASK，2PSK,4PSK,16QAM}4种单载波调制方式来验证所提算法的有效性。假设各调制信号相互独立，各传输多径信道相互独立，且所加高斯白噪声与信号相互独立，在MATLAB2016软件上进行仿真验证。信号参数设置为：载波频率fc为40 MHz，信号码元速率fb为2 Mbit/s，信号采样频率fs为320 MHz，码元个数N为2000，循环频率选取载波频率fc，衰落信道服从瑞利分布。

4.1 仿真实验一

在信噪比(signal noise ratio，SNR)为[-5,10] dB区间范围内，信道选取平坦衰落信道，选取信噪比更新步长为1 dB，分别对不同调制信号独立仿真50次作为训练样本，且在不同信噪比下仿真100次作为测试样本，进行10次独立仿真取平均值作为最终结果输出，结果如图1所示。

图1 不同调制类型的分类曲线

从图1可以看出随着信噪比的不断增加，信号识别率随之上升。在信噪比为-1 dB时，各信号识别率均已达到90%以上，且在3 dB左右时实现了100%识别。且ASK信号相较于相位调制信号识别效果更好。

4.2 仿真实验二

信道性能的好坏是影响接收信号特征的重要因素，故文中选取信号长度为2000，分别采用衰落信道径数为单径，双径和四径，在不同信噪比条件下分别进行10次独立仿真取平均值，得到信号平均识别率，结果如图2所示。

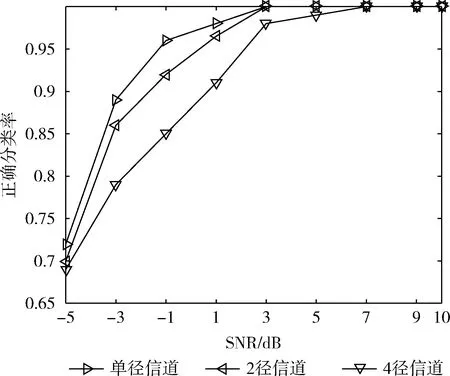
图2 不同信道条件下的分类曲线

从图2可以看出，随着信道数量的增加信号识别率随之减小，但其错误分类概率增加较慢，且随着信噪比的增加其准确识别率均达到90%以上，说明所提出的算法对多径效应具有较好的鲁棒性。

4.3 仿真实验三

数据量的大小对循环累积量特征的提取也会造成不同程度的影响，样本数较少时会影响特征提取的实际值，故文中采用码元个数N=500，N=1000，N=2000这3类数据量对其进行实验，选用单径瑞利衰落信道，不同信噪比条件下独立仿真，得到信号识别率，如图3所示。

从图3可以看出随着数据量的增加信号分类正确率逐渐上升，但对最终的分类效果影响较小，说明所提出的分类算法能够较好反应信号的循环统计特性。

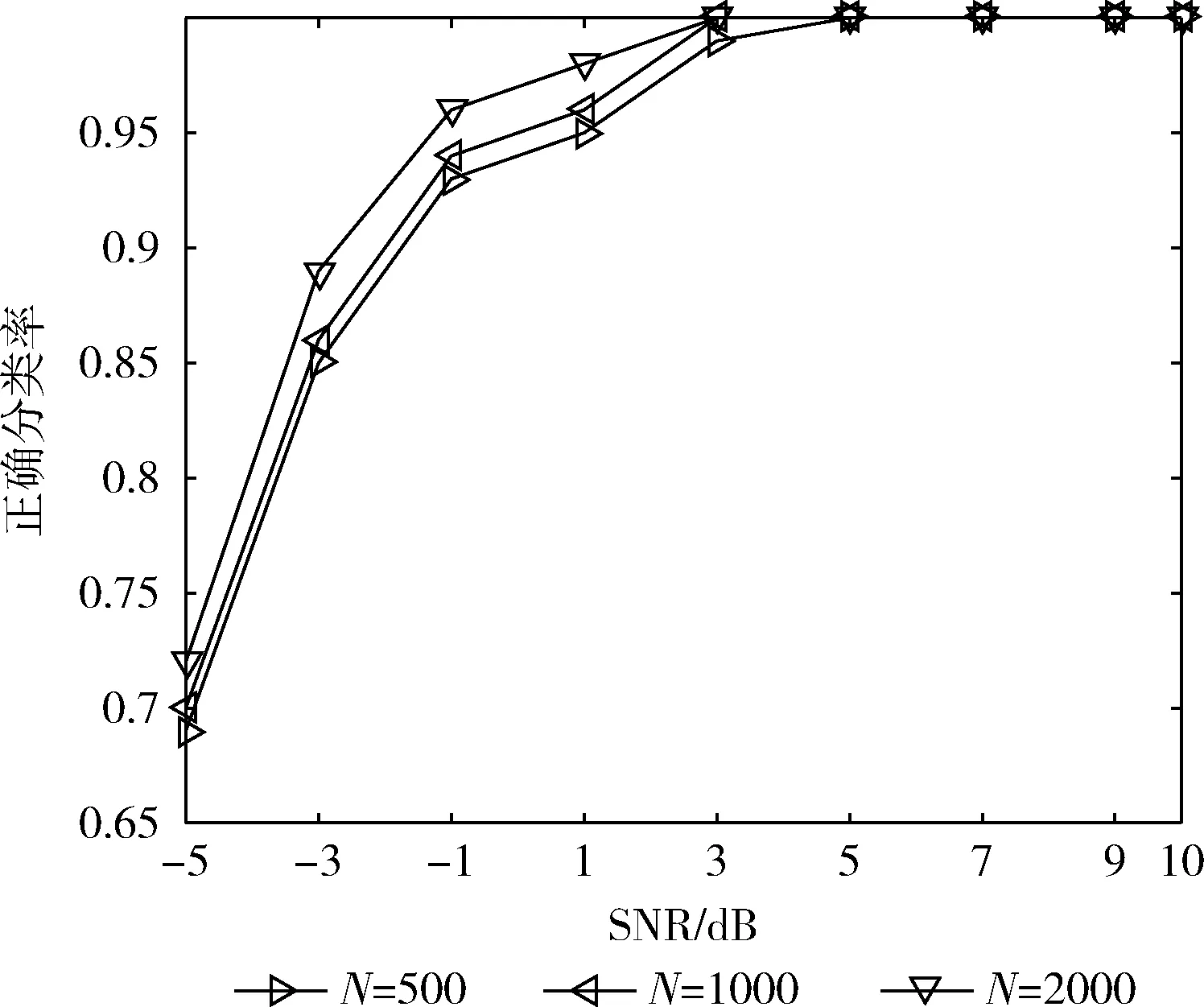
图3 不同数据量对分类性能的影响

从图4可以看出，相较与单个四阶循环累积量特征算法[8]，以及基于高阶累积量的决策树识别算法[4]，本文算法的信号正确识别率相对较高，且在低信噪比条件下也有很好的识别效果，表明本文算法在衰落信道中可以保持良好的识别性能。

图4 衰落信道下不同算法的识别率比较

5 结束语

本文利用循环累积量和优化后的支持向量机实现了对不同类型信号的分类识别。首先通过理论推导证明了特征参数的有效性，之后利用鲸鱼算法对支持向量机进行参数寻优，仿真结果表明，当码元长度为2000时，单径瑞利衰落信道条件下，信噪比为-1 dB时，信号整体识别率均已达到90%。当码元长度变化且信道多径数变化时，算法均有良好分类效果，表明所提出的算法具有较好的抗多径干扰性，提取的信号特征能较好反应信号的循环特性，具有较好的鲁棒性。如何实现对更多类型的信号进行分类以及使用更加有效的分类器仍有待研究，使算法具有更好的应用场景。